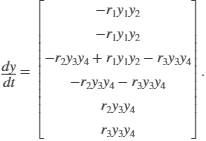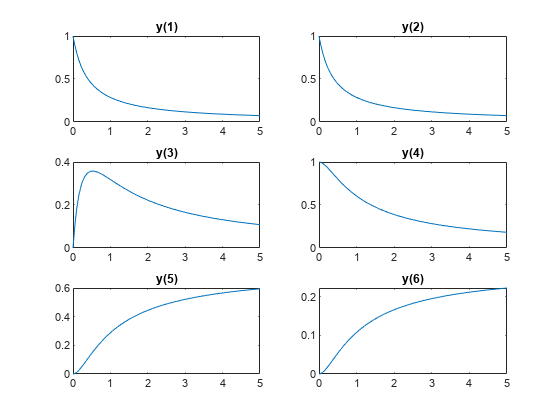MATLAB 拟合线性微分方程组——多反应模型拟合

MATLAB 拟合线性微分方组——多反应模型拟合

---

---

前言

目前我已知可以做微分方程组拟合的软件有 SAS，MATLAB，R ；但是关于软件使用的中文介绍（翻译）并不多，因此记录下来。所做应用为食品生物反应方面，首先根据化学反应建立数学模型，然后进行实验测得数据，结合模型及实验所得数据估计参数，即完成拟合任务。
本文取自官网文档，如有错误望指正。

---

一、软件要求

MATLAB 软件要求为 2019 以上，使用优化工具箱进行拟合，采用方法为最小二乘法。官网文档链接: Fit ODE Parameters Using Optimization Variables ，使用步骤作如下说明。

二、使用步骤

此方法是以问题为基础的 (the problem-based approach);
在MATLAB命令行中输入以下命令打开示例：

需要注意MATLAB软件需要满足版本要求。

1.问题

此实际问题为估计多步反应中真实反应速率的问题。

2.建立模型

反应流程图如下

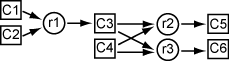
圆圈为反应速率，正方形为反应物。
作出假设：反应速率与反应物的量成比例，则可以建立如下模型：

这里的微分方程组模型是根据反应过程得到的，所得微分方程组能够解释反应过程中各个反应物量的变化。
微分方程组的初值，即各反应物的初值为 $y(0)=[1,1,0,1,0,0]$。

3.用MATLAB表示模型

用函数 diffun() 表示微分方程组

function dydt = diffun(~,y,r)
dydt = zeros(6,1);
s12 = y(1)*y(2);
s34 = y(3)*y(4);

dydt(1) = -r(1)*s12;
dydt(2) = -r(1)*s12;
dydt(3) = -r(2)*s34 + r(1)*s12 - r(3)*s34;
dydt(4) = -r(2)*s34 - r(3)*s34;
dydt(5) = r(2)*s34;
dydt(6) = r(3)*s34;
end

真实的反应速率为 $r_1=2.5，r_2=1.2，r_3=0.45$ ，由此微分方程组调用 ode45 作出0到5时刻的图像，代码如下所示：

rtrue = [2.5 1.2 0.45];
y0 = [1 1 0 1 0 0];
tspan = linspace(0,5);
soltrue = ode45(@(t,y)diffun(t,y,rtrue),tspan,y0);
yvalstrue = deval(soltrue,tspan);
for i = 1:6
    subplot(3,2,i)
    plot(tspan,yvalstrue(i,:))
    title(['y(',num2str(i),')'])
end

4.求解优化问题

4.1 先定义一个由 3 个元素组成的优化变量，需要指定上下边界，

r = optimvar('r',3,"LowerBound",0.1,"UpperBound",10);

4.2 最小二乘法即微分方程组解与真实值之差的平方之和最小，定义一个 RtoODE 函数根据r求解微分方程组，

function solpts = RtoODE(r,tspan,y0)
sol = ode45(@(t,y)diffun(t,y,r),tspan,y0);
solpts = deval(sol,tspan);
end

4.3 用 fcn2optimexpr 把 RtoODE 转化为优化形式的表达式，

fcn2optimexpr

myfcn = fcn2optimexpr(@RtoODE,r,tspan,y0);

4.4 表示最小二乘法，

obj = sum(sum((myfcn - yvalstrue).^2));

4.5 建立优化问题以使用优化工具箱求解，

prob = optimproblem("Objective",obj);

5.求解问题

先给给定 $r_0$ ，此值为待估计参数的猜测值，应尽量接近真实值，使用 solve 求解，

r0.r = [1 1 1];
[rsol,sumsq] = solve(prob,r0)

输出：

Solving problem using lsqnonlin.

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

<stopping criteria details>
rsol = 
    r: [3×1 double]

sumsq = 3.8660e-15

该优化工具箱使用 lsqnonlin 函数拟合。

disp(rsol.r)

输出：

2.5000
1.2000
0.4500

disp(rtrue)

输出：

2.5000    1.2000    0.4500

6.使用有限数据拟合

使用有限数据拟合步骤与上述步骤相同，依然能够拟合，但是拟合效果不如数据完全测得拟合得到的效果好，应尽可能多得得到实验数据。
这里不对此进行详细说明，详细说明请参照官方说明文档。
假设只能观测到 y(5) 和 y(6) ,进行以下拟合：
6.1 定义函数 RtoODE2 只返回第 5,6 个 ODE 输出，

function solpts = RtoODE2(r,tspan,y0)
solpts = RtoODE(r,tspan,y0);
solpts = solpts([5,6],:); % Just y(5) and y(6)
end

6.2 定义新的优化形式的表达式

myfcn2 = fcn2optimexpr(@RtoODE2,r,tspan,y0);

6.3 修改对比数据只包含第 5,6 个输出

yvals2 = yvalstrue([5,6],:);

6.4 定义新的优化问题

obj2 = sum(sum((myfcn2 - yvals2).^2));
prob2 = optimproblem("Objective",obj2);

6.5 求解问题

[rsol2,sumsq2] = solve(prob2,r0)

输出：

Solving problem using lsqnonlin.

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

<stopping criteria details>
rsol2 = 
    r: [3×1 double]

sumsq2 = 2.1616e-05

disp(rsol2.r)
disp(rtrue)

输出：

1.7811
1.5730
0.5899    

2.5000    1.2000    0.4500

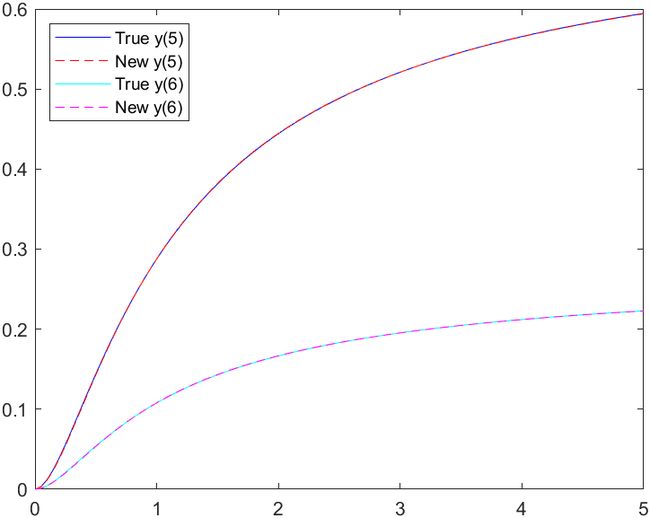
6.6 绘制对比图

figure
plot(tspan,yvals2(1,:),'b-')
hold on
ss2 = RtoODE2(rsol2.r,tspan,y0);
plot(tspan,ss2(1,:),'r--')
plot(tspan,yvals2(2,:),'c-')
plot(tspan,ss2(2,:),'m--')
legend('True y(5)','New y(5)','True y(6)','New y(6)','Location','northwest')
hold off

输出：

6.7 绘制全部对比图

figure
yvals2 = RtoODE(rsol2.r,tspan,y0);
for i = 1:6
    subplot(3,2,i)
    plot(tspan,yvalstrue(i,:),'b-',tspan,yvals2(i,:),'r--')
    legend('True','New','Location','best')
    title(['y(',num2str(i),')'])
end

输出：

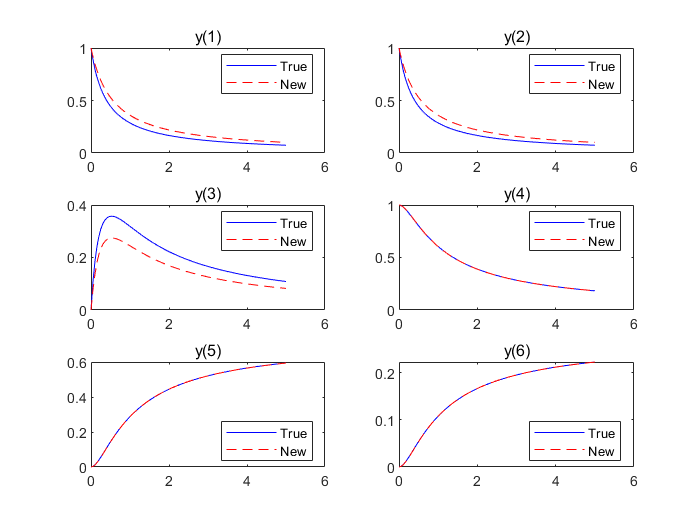
由此可知，应当有尽可能多的观测数据，否则拟合效果可能会有偏差。

---

三、总结

此示例拟合效果较好，因为此示例首先由已知r值求解y值，再根据y值拟合r值，大致类似于自己拟合自己。
经实验拟合检验，此拟合方法适用。

---

如果觉得内容不错，请点赞、收藏、关注