TimesNet：Temporal 2D-variation modeling for general time series analysis 论文要点
文章目录
-
- 摘要
- 问题分析
-
- 数据层面
- 方法层面
- 本文方法
- 整体框架
-
- TimesBlock
-
- 1D to 2D
-
- 选择最显著频率
- 维度转换
- 捕捉2D特征
- 自适应聚合
- 实验结果
-
- 短期预测
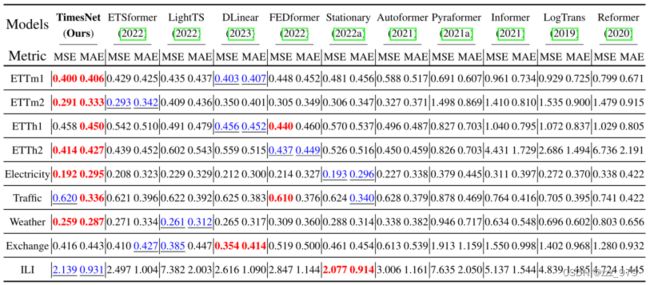
- 长期预测
- imputation
- 分类
- 异常检测
文章获取： https://openreview.net/pdf?id=ju_Uqw384Oq
代码地址： https://github.com/thuml/Time-Series-Library
摘要
时间序列分析在天气预报、异常检测、动作识别等领域有着广泛的应用。时间变化建模是大量分析任务中常见的关键问题。以前的方法试图直接从1D时间序列中完成这一点，由于复杂的时间模式，这是极具挑战性的。通过对时间序列多周期性的观察，我们将复杂的时间变化分解为多个周期内变化和周期间变化。为了解决一维时间序列在表示能力上的局限性，我们将一维时间序列转换为一组基于多个周期的二维张量，从而将时间变化分析扩展到二维空间。这种变换可以将周期内变化和周期间变化分别嵌入到二维张量的列和行中，使得二维变化可以很容易地用二维核来建模。从技术上讲，我们提出了以时间块作为时间序列分析的任务通用骨干的时间网。TimesBlock可以自适应地发现多周期性，并通过参数高效的初始块从转换后的二维张量中提取复杂的时间变化。我们提出的TimesNet在五个主流时间序列分析任务中达到了一致的最先进水平，包括短期和长期预测、imputation、分类和异常检测。
问题分析
数据层面
数据特征上，不同于自然语言、视频等序列数据，时间序列中单个时刻仅保存了一些标量，其关键信息更多地被蕴含在时序变化中
方法层面
近年来，应用于时间序列分析的方法大致可以分为基于卷积的方法和基于transformer的方法
-
基于卷积的方法主要关注捕捉临近时刻之间的变化，在长期依赖上建模能力不足。
-
基于transformer的方法虽然在建模长期依赖上具有天然优势，但是由于现实世界的时序变化极其复杂，仅仅依靠离散时间点之间的注意力难以挖掘出可靠的时序依赖。
本文方法
TimeNet从周期角度出发，从多种不同粒度提取数据在周期内以及周期间的变化
- 将数据进行FFT快速傅里叶变换，找出幅值最高的k个频率，并按照不同频率对数据进行多组采样
- 将同一频率采样的多组数据拼在一起，将数据从一个一维数据转换为多个二维数据
- 使用具有二维核的TimesBlock（基于Inception）对每一组二维数据进行特征提取
- 将k组二维数据的特征使用自适应聚合进行拼接，得到时间序列的整体特征
- 以残差形式多次叠加步骤1-4（TImesBlock）
整体框架
基于时间序列的多周期性，提出了具有模块化架构的时间网，以捕获来自不同周期的时间模式
对于每个周期，为了捕获相应的周期内和周期间变化，在TImesNet中设计了一个TimesBlock，它可以将1D时间序列转换为2D空间，并通过共享参数的InceptionBlock同时对两种类型的变化进行建模
TimesBlock
TimesNet以残差模式组织TimesBlock，可以在二维空间中通过参数高效的Inception Block捕获k个不同的重塑张量的各种时间二维变化，并根据归一化的振幅值进行融合，除第一层外每一个TimesBlock中数据的变化都是1D->2D->1D
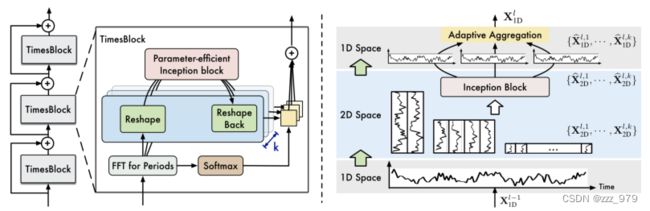
对于第1层，使用嵌入层将原始数据投影到一维深度特征空间
对于第l个TimesBlock，整个过程包括两个连续的部分：捕获时态2d变化和自适应聚合来自不同时期的表示
每一个TimesBlock都需要进行FFT变换，转为2D提取特征，再自适应聚合为1D
1D to 2D
每个时间点与相邻区域同时存在两种时间变化类型，即周期内变化和周期间变化。然而，原始的时间序列一维结构只能表现相邻时间点之间的变化
时间变化的二维结构，它可以明确地表示周期内和周期间的变化，从而在表示能力上更有优势，有利于后续的表示学习
选择最显著频率
有C个长度为T的时间序列，原始1D数据为X1D。为了表示周期间的变化，首先通过快速傅立叶变换(FFT)在频域对时间序列进行如下分析，发现数据周期
FFT(·)和Amp(·)表示FFT和振幅值的计算。A∈RT表示每个频率的计算振幅，由Avg(·)从C维取平均
考虑到频域的稀疏性，避免无意义高频带来的噪声，我们只选取前k个振幅值，得到了非归一化振幅{Af1，···，Afk}的最显著频率{f1，···，fk}，其中k为超参数。这些选定的频率也对应k个周期长度{p1，···，pk}
由于频域的共轭性，只考虑{1，···，[t/2]}范围内的频率
维度转换
基于所选频率{f1 , · · · , fk}和同期长度{p1 , · · · , pk}，可以将一个一维时间序列reshape多个二维张量
实现，若无法恰好根据频率完成采样，则对时间序列填充0到fi*pi长度
二维张量的列、行分别表示pi（长度）和fi（频率），对应周期长度pi下的周期内变化和周期间变化
基于所选择的频率和估计的周期，我们得到了一组二维张量{X12D，···，Xk2D}，它表示了不同周期推导出的k个不同的时域二维变化
二维张量带来了两种类型的位置，即相邻时间点(列，周期内变化)和相邻周期(行，周期间变化)之间的位置。因此，二维核可以很容易地处理时序二维变化
捕捉2D特征
使用参数高效InceptionBlock对2D特征进行捕捉
- 首先获取一个2D数据
- 然后通过FFT转换为多个2D数据
- 转换后，我们通过一个共享参数的inceptionBlock处理2D张量，即inception(·)，使得模型大小对超参数k的选择不变
- 然后我们将学习到的二维表示转换回1D空间进行聚合，其中我们使用Trunc(·)将长度为pi × fi的填充级数截断为原始长度T
自适应聚合
作用：融合k个不同的1D表示
振幅A可以反映所选频率和周期的相对重要性，从而对应于每个转换的2D张量的重要性，因此基于振幅聚合1D表示
实验结果
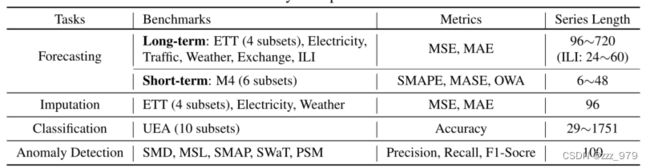
为了验证TimesNet的通用性，对5个主流分析任务进行了广泛的实验，包括短期和长期预测、imputation、分类和异常检测。
短期预测
长期预测
imputation
分类
异常检测
