【马蹄集】—— 百度之星 2023

百度之星 2023

---

BD202301 公园⭐

难度：钻石    时间限制：1秒    占用内存：64M

题目描述

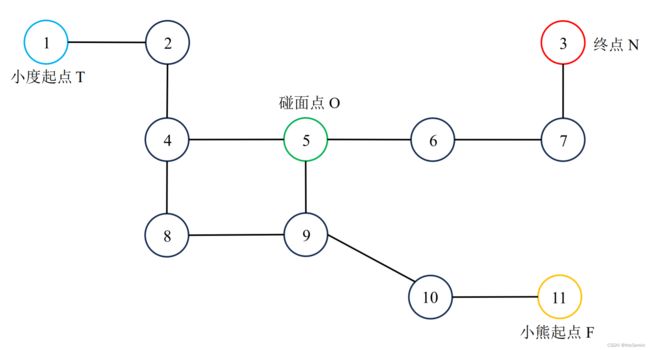
今天是六一节，小度去公园玩，公园一共 $N$ 个景点，正巧看到朋友圈度度熊也在这个公园玩，于是他们约定好一块去景点 $N$。小度当前所在景点编号为 $T$，从一个景点到附近的景点需要消耗的体力是 $TE$，而度度熊所在景点编号为 $F$，移动消耗为 $FE$。好朋友在一块，赶路都会开心很多，所以如果小度和度度熊一块移动（即在相同位置向相同方向移动），每一步他俩的总消耗将会减少 $S$。

求他俩到景点 $N$ 时，所需要的总消耗最少是多少?

格式

输入格式：
第一行三个数值 $TE,FE,S$，分别代表小度移动消耗值，度度熊移动消耗值，一起移动的消耗减少值。$1\le TE,FE,S\le 4000,S\le TE+FE$；
第二行四个数值 $T,F,N,M$，分别代表小度出发点，度度熊出发点，目标节点，总路径数。$1\le T,F,N,M\le 40000$。
接下来 $M$ 行，每行两个整数 $X,Y$，代表连通的两个景点。$1\le X,Y\le N$。
输出格式：
一个整数，即总消耗最小值。如果不能到达 $N$，输出 -1。

样例 1

输入：
4 4 3
1 2 8 8
1 4
2 3
3 4
4 7
2 5
5 6
6 8
7 8

输出：

22

相关知识点：广度优先搜索

题解

这道题给出了各点之间的可达关系和代价（不同角色的代价不同），最终要求出两个人到终点所需消耗的最低能量。对于这种点之间为可达关系而不是距离的走迷宫问题，其对应图的邻接关系通常是个稀疏阵，这时，切不可用二维数组来存放该图，而要用邻接表。一方面可避免爆内存的风险，另一方面则能大大加快对图的搜索速度。

接下来我们思考如何寻找具有最低能耗的路线。由于题目指出“如果小度和度度熊一块移动，每一步他俩的总消耗将会减少”，因此从贪心的角度出发，自然是越早碰面越有利于降低总能耗。但是，存在一种情况，即在追求“尽早碰面”的过程中付出了巨大代价，那么这样的碰面还不如各自走自己的。因此，对本题寻找最低能耗的路线而言，很难通过贪心的思路来求解。

在这样的情况下，最简单有效的办法就是枚举。即逐个枚举中间节点作为碰面点，并以此计算在这种方案下的总能耗。最终，输出所有方案里的最低能耗即可。由于每次枚举一个点作为见面点时，都需要计算 T 和 F 到 O 的距离，以及 O 到 N 的距离。为了降低时间开销，我们可事先算出 T、F 到其余各点的距离，以及各点到终点 O 的距离。这样一来，每次在枚举时就不再需要单独计算各段距离，而是直接取值。

下面直接给出基于以上思路得到的求解本题的完整代码：

/*
    BD202301 公园 
    深度优先搜索 
*/
#include 
using namespace std; 

const int MAX = 4e4+5;
// 存放各点之间的可达关系（稀疏阵） 
vector<int> v[MAX];
// 分别存放从T、F 和N到其他所有点之间的最短距离
int pt[MAX], pf[MAX], pn[MAX];

// 计算从 start 出发到其余所有点的最短距离
void bfs(int start, int dis[])
{
    // 初值统一赋为一个较大的值
    for(int i=0; i<MAX; i++) dis[i] = MAX;
    // 广度优先搜索求最短距离 
    queue<int> q; 
    q.push(start); 
    dis[start] = 0;
    while(!q.empty()){
        int cur = q.front(); q.pop();
        // 遍历邻接点 
        for(int i=0; i<v[cur].size(); i++) {
            int neighbor = v[cur][i]; 
            if(dis[neighbor] > dis[cur]+1) {
                q.push(neighbor);
                dis[neighbor] = dis[cur] + 1;
            }
        }
    }
}

int main()
{
    // 获取输入
    int TE, FE, S, T, F, N, M, X, Y;
    cin>>TE>>FE>>S;
    cin>>T>>F>>N>>M;
    for(int i=0; i<M; i++){
        cin>>X>>Y;
        v[X].push_back(Y);
        v[Y].push_back(X);
    }
    // 寻找从小度（T）、小熊（F）到其余各点的最短路径以及各点到目的地（N）的最短距离 
    bfs(T, pt), bfs(F, pf), bfs(N, pn);
    // 若两个点都无法到达终点，则输出 -1 
    if (pt[N] == MAX || pf[N] == MAX)
        cout<<"-1"<<endl;
    else{
        // 最坏情况下各自单独去终点 
        int ans = pt[N] * TE + pf[N] * FE, tmp; 
        // 枚举所有点作为见面地点，查找是否存在更低的能量消耗情况 
        for (int i = 1; i < N; i++) { 
            tmp = pt[i] * TE + pf[i] * FE + pn[i] * (TE+FE-S);
            ans = min(ans, tmp);
        }
        cout<<ans<<endl;
    }
    return 0;
} 

---

BD202302 蛋糕划分⭐⭐⭐

难度：星耀    时间限制：1秒    占用内存：64M

题目描述

小度准备切一个蛋糕。这个蛋糕的大小为 $N\times N$，蛋糕每个部分的重量并不均匀。

小度一共可以切 $K$ 刀，每一刀都是垂直或者水平的，现在小度想知道在切了 $K$ 刀之后，最重的一块蛋糕最轻的重量是多少。

格式

输入格式：第一行包含 $N$ 和 $K$。其中：$2\le N\le 15,1\le K\le 2N-2$；
     第二到第 $1+N$ 行每行 $N$ 个数字，描述这一行蛋糕每个位置的重量 $W$ 。其中：$0\le W\le 1000$。
输出格式：输出一个整数，最重的一块蛋糕最轻是多少。。

样例 1

输入：

3 2
1 1 2
1 1 2
2 2 5

输出：

5

相关知识点：贪心、二分查找、二维前缀和

题解

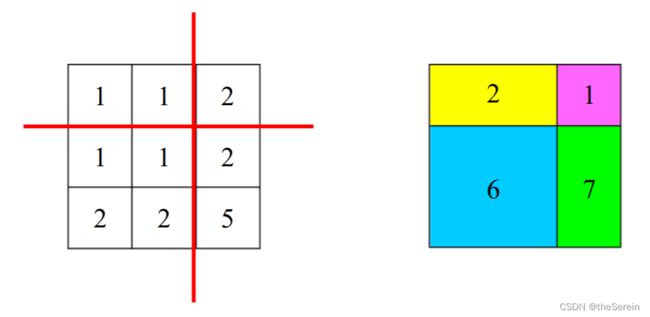
首先要充分理解题目所说 “最重的一块蛋糕最轻的重量是多少” 的含义。对一个蛋糕按其固有分块线进行切割，势必会得到若干子块，在这些子块中肯定有一个重量最大的。例如，对如下蛋糕采取图示切割方案时，得到四个子块中重量最大的为 7：

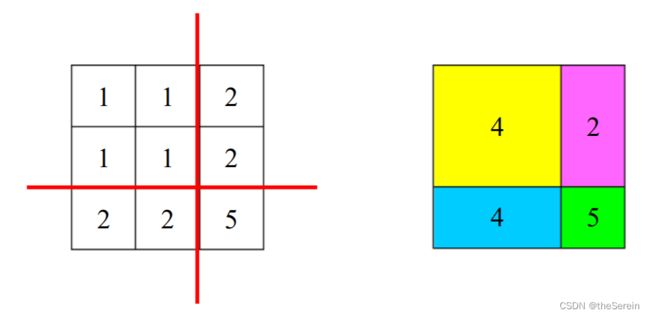
但是，我们发现还存在一种切割方式能降低最重子块的重量：

还有没有能继续降低最重子块重量的切割方案呢？对本题而言，这是最终解，于是输出 5。

基于此可知，最简单的做法就是枚举全部的切割方案，并算出各方案下的最重子块，然后取这些最重质量中的最小值即可。但是，极限情况下，最多的切割方案高达 $C_{{14}^2}^{28}=C_{196}^{28}$ 种，必定超时。因此我们不能直接对切割方案进行线性枚举。这时候通常要想到二分法，但此时二分的目标将变为“最重子块的重量”。即寻找一个重量，使得不存在任何切割方案能切出比该重量更低的子块蛋糕。从题目给出的数据可知，极限情况下最大的重量为 $1000\times 15\times 15$（即，整个蛋糕各子块均为最大重量 1000，且一刀不切）。这在 ${\log }_{2}x$ 级下，将不会超过 17 次枚举。这样一来，我们就将原任务转换为“给定一个重量，问是否存在一种切割方式使得其切出的各子块都不大于该值”。而该过程最多进行 17 次。

现在我们思考，如何判断某个重量是否存在一种满足以上要求的切割方案。这还是涉及到对蛋糕进行切割的问题。但是我们现在不需要求“指定切割次数下的各切割方案”，而是找一种满足要求的解。这是一个证存在的问题，因此我们可采取贪心的思路进行求解。

整体的切割思路如下：

1. 按行枚举切割方案；
2. 对每一个按行切割的方案按列进行切割，并统计切割得到的子块重量。在切割满足要求的情况下（即总的切割次数不能超过 $K$），算出切割出的各子块重量。若存在被切割出的子块重量超过二分法给定的重量限制，则说明当前切割方法是不成立的，于是跳过此列切割并继续查找（这一操作类似剪枝的作用，直接否定了一类切割方案，大大降低枚举次数）。若能从某一次列切割中顺利遍历全部列（即表示找到了一个切割方案使得其切出的所有子块重量均小于二分法给定的重量限制），则直接返回真。
3. 枚举结束，说明没有找到任何切割方法能使最重的一块蛋糕最轻的重量小于给定值，则返回假。

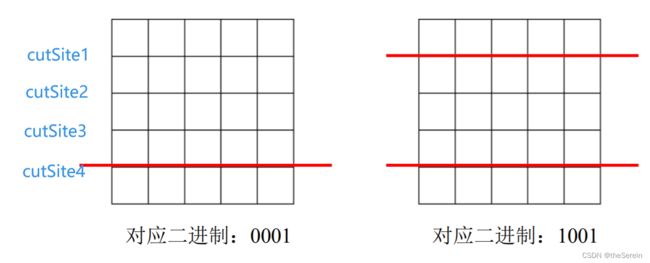
下面介绍如何按行枚举切割方案。注意到一件事，对于一个长度为 $n$ 的格子，其形成的空隙数量为$n-1$ ，这就是说有 $n-1$ 个位置可进行切割。对每个位置有切与不切两种选择，因此由这 $n-1$ 个位置可产生的切割方案共有 $2^{n-1}$ 种。实际上，这 $2^{n-1}$ 种不同的切割方案正好可用其对应的二进制位来表达，如下图所示。而由十进制数转换为二进制数的过程正好可用于记录该数对应的切割方案。需要注意的是，在枚举按行切割的方案数时，一旦某种方案的切割次数超过了给定的切割次数 $K$ 时，就需要直接跳过此切割方案（这也相当于是进行剪枝）。

有了具体的横向切割方案，接下来便能根据贪心的思想来寻找满足“使切出的子块均不大于给定重量”这一要求的切割方案，具体的流程如下：

1. 遍历全部列（尝试在纵向进行划分，包括了不对列进行切割的情况）；
2. 对每一列，从上到下计算其在当前横向切割方案下的产生的全部子块重量（这一步涉及到求矩阵元素和的操作）。由于我们要使“最重的一块蛋糕最轻”，因此我们在这一步求解时，需要在满足重量不大于给定值的前提下尽可能重（即贪心）。在这样的前提下，我们动态向右累加子块重量，一旦某次添加的列（单列块）使得该子块重量已经超过给定重量，则表示必须在此列前的位置切割，否则那样的切割方案必定不满足要求。另外，若“单列块”本身的重量超过了给定重量，则基于目前行切割方案进行的任何切割都不可能得到满足条件的切割方式，这种情况下可直接跳过目前的行切割方案（为此，需要单独设计一个标记变量）。

在上述枚举过程中，涉及到一个求二维矩阵中子阵元素之和的过程（即计算子块的重量）。显然，我们不可能每次都单独算子阵元素和。于是，这就需要用二维前缀和数组。有关二维前缀和的构建和求和在前面已经讲过，在此就不过多赘述（二位前缀和数组传送门）。

本题是一道综合性非常强的例题，涉及到二分法查找、贪心、二维前缀和等相关知识，是一道非常值得练习的题目！

下面直接给出基于以上思路得到的求解本题的完整代码：

/*
    BD202302 蛋糕划分 
    贪心、二分查找、二维前缀和 
*/
#include 
using namespace std; 

const int N = 20;
int n, K, maxQuality;
int ary[N][N], prefixAry[N][N];

// 根据二维前缀和数组计算子块和
int getPrefixSum(int max_x,int max_y,int min_x,int min_y)
{
    return prefixAry[max_x][max_y] - prefixAry[min_x-1][max_y] - prefixAry[max_x][min_y-1] + prefixAry[min_x-1][min_y-1];
}

// 判断在 K 刀之内是否存在一种切割方案使得所有蛋糕的质量都小于 quality
bool check(int quality)
{
    // 如果最重的子块比 quality 大，则不可能存在切割方案使各块小于 quality
    if(maxQuality > quality) return false;
    // 纵向切割方案对应的二进制表达形式容器
    int col[N] = {0};
    // 横向切割时，对应子块的累计元素和，以及该位置的元素值
    int sum_col[N], cur_col[N];
    // 枚举横向切割的方案（n 个块之间有 n-1 个切割位置，对应就有 2^(n-1) 种切割方式）
    int limit = 1 << (n-1), tmp, pos, cutCnt;
    for(int i=0; i<limit; i++){
        // 切割点容器
        vector<int> v;
        tmp = i;
        // 记录切割位置
        pos = 0;
        // 记录切割次数
        cutCnt = 0;
        // 取出十进制数 i 对应的二进制编码中所表示的切割方案
        while(tmp){
            pos ++;
            if(tmp & 1){
                v.push_back(pos);
                cutCnt++;
            }
            tmp /= 2;
        }
        // 如果该切割方案的切割次数超过了 K 则跳过
        if(cutCnt > K) continue;
        v.push_back(n);
        
        // 不合适的横向切割标记，用于提前跳出一些始终不满足要求的横向切割方案 
    	int fail = 0;
        // 初始化
        memset(col, 0, sizeof(col));
        memset(cur_col,0,sizeof(cur_col));
        memset(sum_col,0,sizeof(sum_col));
        int top;
        // 按列枚举被横向切割的蛋糕质量，如果超过了 quality 就必须进行切割
        for(int j=1; j<=n; j++){
            // 当前块的最小行下标
            top = 1;
            // 对于第 j 列，从上到下枚举计算其产生的子块
            for(int k=0; k<v.size(); k++){
                // 当前块的最大行下标
                int down = v[k];
                // 当前宽度为 1 的块的重量
                int now = getPrefixSum(down,j,top,j);
                // 若切割得到子块的质量位超过 quality 就需要重新切割
                if(now > quality){
                    fail = 1;
                    break;
                }
                // 否则就继续沿横向累加
                sum_col[k] += now;
                // 缓存当前列的数据，防止被切以形成新块
                cur_col[k] = now;
                // 若前一列为切割点，则说明当前列的上层块已经满足切割条件，则重新开启新列计数 
                if(col[j-1])
                    sum_col[k] = now;
                // 第 j 块 i 列累加超过了 quality，说明当前列不能被累加，因此需进行切割
                if(sum_col[k] > quality)
                {
                    // 记录竖切位置
                    col[j-1] = 1;
                    sum_col[k] = now;
                    // 更新 k 横块以上的第 j 列的重量，不再累加前面的
                    for(int p=0; p<k; p++)
                        sum_col[p] = cur_col[p];
                }
                // 更新最小行的行号
                top = down+1;    
            }
            if(fail == 1) break;
        }
        if(fail == 1) continue;
        // 遍历完整个列切割过程，累加列切割次数 
        for(int p=1; p<n; p++)
			if(col[p]) cutCnt++;
		// 若总切割次数不大于 K 则说明找到一个满足要求的切割方案 
        if(cutCnt <= K) return true;
    }
    // 不存在任何切割方案满足要求 
    return false;
}

int main()
{
    // 获取输入
    cin>>n>>K;
    for(int i=1; i<=n; i++)
    	for(int j=1; j<=n; j++){
    		cin>>ary[i][j];
    		maxQuality = max(maxQuality, ary[i][j]);
    		// 构建二维前缀和数组
    		prefixAry[i][j] = ary[i][j] + prefixAry[i-1][j] + prefixAry[i][j-1] - prefixAry[i-1][j-1];
		}
	// 二分查找一个质量，使得该质量是划分能得到的最小值
	int l = 0, r = 1000*15*15, m;
	while(l <= r){
	    m = (l+r) >> 1;
	    // 若存在一种切法使所有块都小于 m,说明还存在更小切块的方案
	    if(check(m)) r = m-1;
	    // 否则说明当前切法是在保证质量尽可能大的情况下的最小切割方案
	    else l = m+1;
	}
	// 输出结果
	cout<<l<<endl;
	return 0;
}

---

BD202303 第五维度⭐⭐

难度：星耀    时间限制：1秒    占用内存：64M

题目描述

零维是点，点动成线；
一维是线，线动成面；
二维是面，面动成体；
三维是体，体动成史；
四维是史，史动???
现在人类企图理解第五维度。
小度是第五维度的一位智者。一天，小度发现人类的许多科学家在试图理解第五维度，人类是四维生物，若是他们理解了第五维度，很可能也会到来第五维度的空间，这显然是小度不愿意看到的（毕竟哪里都有人口数量的问题….）所以小度希望他们尽可能晚的理解第五维度，因此，小度用更高维度的视角把所有人类中在理解第五维的科学家都看到了，而这些科学家的智商会不一样，所以他们的理解速度 $V_i$ 也会不一样；并且，他们开始理解的时间点 $S_i$ 也不一样。理解速度 $V_i$ 描述为每过单位时间可获得 $V_i$ 个单位理解力，也就是说在 $S_i+1$ 的时间点该科学家会第一次贡献 $V_i$ 的理解力。我们定义理解力总数超过 $m$ 时理解了第五维度。 小度因为维度更高，可以使用时间悖论来给人类一次重大的打击，小度可以让任意一位科学家在任意一个时间点消失，所以他接下来的理解不会继续；而且人类不会记得他，所以他之前的贡献会消失。因为小度能力有限，所以小度只能使用一次暂时悖论。

现在求在尽可能晚的情况下，人类理解第五维度的最早时间点。时间点初始为 0，但显然，没有科学家能够在 0 时刻有贡献。

格式

输入格式：第一行给出一个整数 $n$ 和一个整数 $m$，表示有 $n$ 个科学家，在理解力总数超过 $m$ 时理解了第五维度；
     第二行至第 $n+1$ 行：每行两个整数 $S_i$ 和 $V_i$ 。
     对于 100% 的数据：$1\le n\le {10}^5，m\le 2\times {10}^9，0\le S_i\le 2\times {10}^9，0\le V_i\le {10}^3$。
输出格式：一行，包含一个整数 $T$ 表示在尽可能晚的情况下，人类理解第五维度的最早时间点。若人类永远无法理解第五维度，则输出 -1。

样例 1

输入：
3 10
0 1
4 6
5 1

输出：

8

样例 2

输入：
3 10
0 0
4 0
5 1

输出：

-1

备注

对于第一个样例，使得 $S_i=4，V_i=6$ 的科学家消失，则每个时刻总共理解力为：0 1 2 3 4 5 7 9 11，在时刻 8 超过 $m=10$，因此输出 8；对于第二个样例，人类永远无法理解第五维度，因此输出 -1 。

相关知识点：贪心

题解

首先对本题的意思进行一个简化：输入 $n$ 个科学家开始理解第五维度的时间点 $S_i$ 以及其单位时间能得到的理解力 $V_i$ （均为非负整数），那么随着时间的推移，全部科学家的总理解力肯定是不断增加的。一旦总理解力达到了 $m$ ，则认为人类能理解第五维度。但是，现在有一个具有上帝视角的人，他总能找到在这些科学家中具有最高理解力的那位并将其从抹除（则他的理解力也将消失），那么这时候人类还能理解第五维度么？如果能，则输出在这样的前提下人类理解第五维度的最早时间；否则输出 -1。

本题中，$m$ 的最大取值为 $2\times {10}^9$ ，那么在极限情况下（只有一个科学家且 $S_i=0,V_i=1$）的最长时间也是 $2\times {10}^9$ 。可以看出，如果直接枚举时间线算出人类的总理解力，并在抹除具有最高理解力的人后判断与 $m$ 的大小关系是极易超时的。在这种情况下，一定要敏锐地想到二分法查找。

对于每一次查找的时间 $T$，可采取下式求解全部人类的总理解力：

for(int i=0; i<n; i++){
        if(T > S[i]){
            // 累加
            sum_comp += ((long long)T - S[i]) * V[i];
        }
}

注意，题目要求在尽可能晚的情况下，人类理解第五维度的最早时间点。而尽可能晚，就意味着每次都要抹除此刻对人类理解力共享最大的科学家。为此，我们可以在求全部人类总理解力的同时，记录其中的最大理解力，并在最后减去该值即可，于是有：

// 判断在指定时间下，人类能否理解第五维度
bool check(int T)
{
    // 在指定时间下人类的理解力总和、这些理解力中的最大值 
    long long sum_comp = 0, max_comp = 0, tmp;
    // 计算所有人的理解力总和，并找到其中的最大值
    for(int i=0; i<n; i++){
        if(T > S[i]){
            // 计算当前第 i 个人的获取的理解力 
            tmp = ((long long)T - S[i]) * V[i];
            // 累加
            sum_comp += tmp;
            // 找出具有最大贡献的理解力 
            max_comp = max(max_comp, tmp);
        }
    }
    // 要求尽可能晚的情况下，那就把具有最大共享的理解力去除即可 
    return (sum_comp - max_comp > m);
}

下面给出基于以上思路得到的求解本题的完整代码：

/*
    BD202303 第五维度 
    贪心、二分法
*/ 

#include 
using namespace std;

const int N = 1e5+5;
// 各科学家的理解力起始数组、单位时间增长数组 
int S[N], V[N];
// 科学家数量和需要理解五维空间的总理解力
int n, m; 

// 判断在指定时间下，人类能否理解第五维度
bool check(int T)
{
    // 在指定时间下人类的理解力总和、这些理解力中的最大值 
    long long sum_comp = 0, max_comp = 0, tmp;
    // 计算所有人的理解力总和，并找到其中的最大值
    for(int i=0; i<n; i++){
        if(T > S[i]){
            // 计算当前第 i 个人的获取的理解力 
            tmp = ((long long)T - S[i]) * V[i];
            // 累加
            sum_comp += tmp;
            // 找出具有最大贡献的理解力 
            max_comp = max(max_comp, tmp);
        }
    }
    // 要求尽可能晚的情况下，那就把具有最大共享的理解力去除即可 
    return (sum_comp - max_comp > m);
}

// 二分查找使科学家能理解的最早时间 
int BinarySearch()
{
    // 能理解的极限情况下，只有 1 个科学家，理解力最小为 1，则最长的时间为 2e9
    long long l = 1, r = 2e9;
    int ans = -1;
    // 二分查找 
    while(l < r){
        int mid = l+r >> 1;
        // 判断该时间下（尽可能晚），人类能否理解第五维度
        if(check(mid)){
            r = mid;
            ans = mid; 
        }else{
            l = mid + 1;
        } 
    }
    return ans;
}

int main( )
{
    // 录入数据 
    cin>>n>>m;
    for(int i=0; i<n; i++)
        cin>>S[i]>>V[i];
    // 输出使科学家能理解的最早时间
    cout<<BinarySearch()<<endl;
    return 0;
}

END

---