算法学习———二叉树（Java版）

本周leetcode刷题路线：

二叉树算法题常用方法：递归算法

        递归算法基本思路：只考虑部分，不考虑整体；

101. 对称二叉树（简单）：

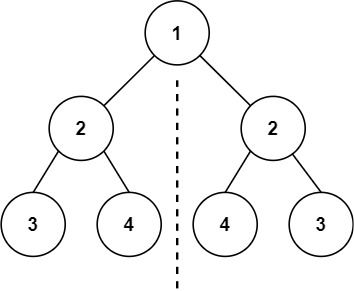
        题目描述： 给你一个二叉树的根节点 root， 检查它是否轴对称。

        示例：

               输入：root = [1, 2, 2, 3, 4, 4, 3]

               输出：true

        解题思路：

        检查该二叉树是否为对称二叉树，即检查该二叉树根节点的左子树翻转后是否与右子树相等（226. 翻转二叉树）。

        将二叉树的左子树翻转后，将其每个节点与右子树对应位置的节点进行比较，只有当两个子树都能顺利递归到末尾时，该二叉树才是对称二叉树。

        解题代码：

class Solution {
    Queue queue = new LinkedList<>();
    public boolean isSymmetric(TreeNode root) {
        func(root.left);
        return judge(root.left, root.right);
    }
    void func(TreeNode node){
        if(node == null)
            return;
        TreeNode temp;
        temp = node.left;
        node.left = node.right;
        node.right = temp;
        func(node.right);
        func(node.left);
    }
    boolean judge(TreeNode node1, TreeNode node2){
        if(node1 == null && node2 != null)
            return false;
        if(node1 != null && node2 == null)
             return false;
        if(node1 == null && node2 == null)
            return true;
        if(node1.val != node2.val)
            return false;
        return judge(node1.left, node2.left) && judge(node1.right, node2.right) ? true : false;
    }
}

---

---

112. 路径总和 （简单）：

        题目描述：  

        给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

        叶子节点 是指没有子节点的节点。

        示例：

         

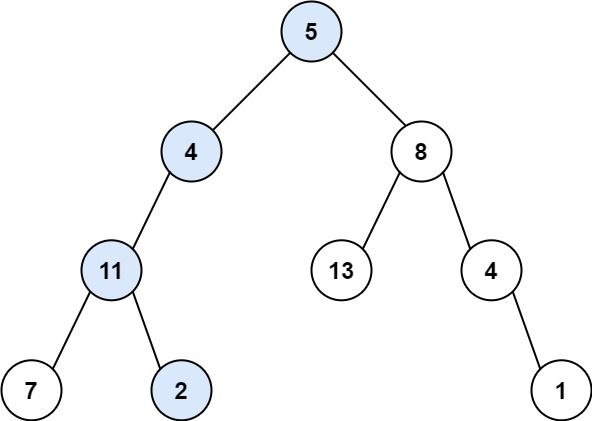
                输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
                输出：true
                解释：等于目标和的根节点到叶节点路径如上图所示。

        解题思路：

        由上而下递归遍历二叉树，每遍历到一个节点就更新targetsum的值为 targetsum -= node.val，当遍历完二叉树的某一分支并且恰好此时 targetsum 的值为零时，说明该路径存在。

        解题代码：

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root == null){
            return false;
        }
        if(root.left == null && root.right == null)
            return root.val - targetSum == 0;
        return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
    }
}

---

---

235. 二叉搜索树的最近公共祖先（中等）：

        题目描述：

        给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

        示例：

                输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
                输出: 6 
                解释: 节点 2 和节点 8 的最近公共祖先是 6。
        解题思路：

        二叉搜索树的特点：若二叉树的某一结点存在左右节点，那么该节点的值大于左节点而小于右节点。

        利用二叉搜索树的特点，我们可以找出p，q节点的大致位置，即当 root.val 同时大于 p.val 和 q.val 时，可以知道 p，q 在 root 节点的左边；反之，在 root 节点右边。从而进一步得出，当 root.val 与 p.val 和 q.val 之差的乘积为负数或等于零时，该节点即为p，q的最近公共祖先。

        解题代码：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if ((long)(root.val - p.val)*(root.val - q.val) <= 0) 
            return root;
        else if (root.val < p.val && root.val < q.val) 
            return lowestCommonAncestor(root.right, p, q);
        else 
            return lowestCommonAncestor(root.left, p, q);
    }
}

---

---

236. 二叉树的最近公共祖先（中等）：

        题目描述：

        给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

        示例：

                

                输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
                输出：5
                解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

        解题思路：

        本题基本思路与 968. 监控二叉树（困难）类似。

        递归遍历二叉树至最底层，寻找p，q所在位置。若没找到，返回null；若找到，返回p，q的值。当两个返回值出现在同一层递归的 left 和 right 中，说明该节点为p，q的最近公共祖先。

        该种解法对于 235. 二叉搜索树的最近公共祖先（中等）同样适用。

        解题代码：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return root;
        }
        if (root == p || root == q) {
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if (left != null && right != null) {
            return root;
        } else if (left != null) {
            return left;
        } else if (right != null) {
            return right;
        }
        return null;
    }
}

---

---

404. 左子树之和（简单）：

        题目描述：

        给定二叉树的根节点root，返回所有左子叶之和。

        示例：

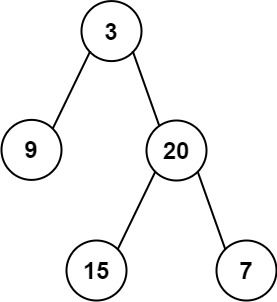
                输入: root = [3,9,20,null,null,15,7] 
                输出: 24 
                解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24 

        解题思路：

        递归遍历二叉树的所有节点，若该节点存在左子叶，则将其保存在变量 left 中，遍历完所有节点后，left 的值即为该二叉树所有左子叶的和。

        解题代码：

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        int left = 0;
        if(root == null)
            return 0;
        if(root.left != null && root.left.left == null && root.left.right == null)
            left += root.left.val;
        return left + sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
    }
}

---

---

572. 另一棵树的子树（简单）：

        题目描述：

        给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

        二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

        示例：

                输入：root = [3,4,5,1,2], subRoot = [4,1,2]

                输出：true

        解题思路：

               判断树 subRoot 是否为树 root 的子树，即判断在每个节点的值都相等的情况下是否能同时递归至叶子节点，即树的末尾。若能，则 subRoot 是 root 的子树；若不能，则不是。

        解题代码：

class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null)
            return false;
        return func(root, subRoot) || isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
    }
    public boolean func(TreeNode root, TreeNode subRoot){
        if(root == null && subRoot == null){
            return true;
        }
        if(root == null || subRoot == null){
            return false;
        }
        if(root.val != subRoot.val)
            return false;
        return func(root.left, subRoot.left) && func(root.right, subRoot.right);
    }
}

---

---

学习心得：​​​​​​​二叉树结构是由链表演变而来的一种数据结构，用途多样；同时，递归是二叉树算法题的常用解法，若对递归理解不够透彻，在解决二叉树算法题的时候会寸步难行，因此二叉树算法题的门槛比较高。在本星期的算法学习中，我对于二叉树的结构有了深刻的认识，了解了几种对于二叉树的递归结构，但还是不够熟练，不能立刻分析出应该用哪种结构，因此还需多加练习巩固递归算法。