用VBA实现对一维数组的排序(5)归并排序
归并排序涉及到递归,很多人都觉得这是一个难点,但是在我看来,这就是一层窗户纸捅破了就通了.
先说递归:百度词条解释:” 是指函数/过程/子程序在运行过程序中直接或间接调用自身而产生的重入现象”这句话什么意思呢?引用一个故事就清楚了:从前有座山,山上有座庙,庙里一老和尚一小和尚,老和尚给小和尚讲故事:从前从前有座山,山上有座庙,庙里一老和尚一小和尚,老和尚给小和尚讲故事, 从前有座山,山上有座庙,庙里一老和尚一小和尚,老和尚给小和尚讲故事, 从前有座山,山上有座庙,庙里一老和尚一小和尚,老和尚给小和尚讲故事……
画成图就是
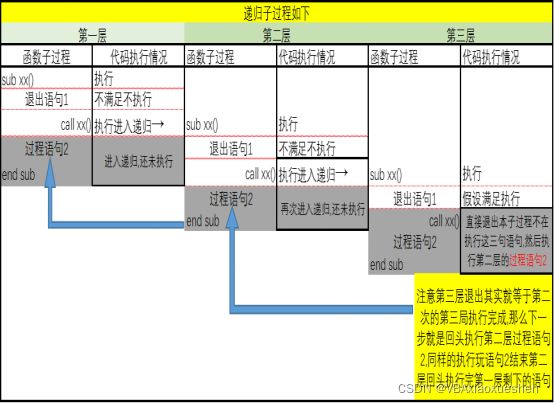
上图的递归没有退出机制,这样很容易就造成栈溢出,而下图则清楚的说明了机油退出机制的递归流程.
在实际过程中,可能会有很多层递归,但是无论多少层,如果不设置退出语句,那么递归不会停止一直递归下去,这样就会导致栈溢出.如果设置了退出语句,但是迟迟没有触发该语句,也会导致栈溢出,所以没事别用递归,有可能退出语句没来得及触发就栈溢出了.这个问题还没法计算,有可能前面的数据用得好好地,后面数据变大了就溢出了.
我们再回想一下这个故事,它可以一直就这么被讲下去而不停止,但如果我们加一句”庙里没来香客”故事就有可能因为香客的到来而被打断:从前有座山,山上有座庙 ,庙里一老和尚一小和尚,庙里没来香客,老和尚就给小和尚讲故事,故事讲完小和尚就要去睡觉,老和尚就讲: 从前有座山,山上有座庙 ,庙里一老和尚一小和尚,庙里没来香客,老和尚就给小和尚讲故事,故事讲完小和尚就要去睡觉,老和尚就讲: 从前有座山,山上有座庙 ,庙里一老和尚一小和尚,庙里没来香客,老和尚就给小和尚讲故事,故事讲完小和尚就要去睡觉,老和尚就讲: 从前有座山,山上有座庙 ,庙里一老和尚一小和尚,庙里突然来了一个女施主,老和尚吓唬小和尚:这是狐狸变得会吃人,赶紧去睡觉.
故事就这么结束了?可没有,最后一个故事小和尚去睡觉了,此时倒数第二个故事里面的老和尚讲完了这他讲的故事,小和尚也该去睡觉了,再紧接着倒数第三个故事里面的老和尚讲完了他的故事,小和尚也该去休息了,直到最后一个小和尚睡觉才是真的结束.这就是递归
接下来我们来看看归并排序是怎么完成排序的,先看一个特殊案例.
特殊案例的特殊性就在于,这组数据是我特地取的: 2,6 ,7,10,21,0,3,5,15,14,23一共是11个数字,其中左半部分的2,6 ,7,10,21和右半部分的0,3,5,15,14,23是两个分别排好序的数据串.但整体2,6,7,10,21,0,3,5,15,14,23又不是排好序的数据串,现在我们将其排序,看上图.
第一步:取一个同等大小的数组.
第二步:取三个变量a,b,c作为指针,
第三步:开始对比,对比过程看下图
图片的过程演示得很清楚了,不在画蛇添足再解释了.现在的问题是特殊案例我们能搞定,但是实际中不可能每天都有特殊案例,甚至特殊案例都有可能一辈子也不出现.此时又该怎么处理呢?
答案很简单,换个角度思考问题:两个数字组成一个数字串,或是只有单独一个数字的的时候,我们其实就可以将其视为一个特殊案例,这么一来,我们只需要做一件事情就可以将数组分解为一小组一小组的特殊案例然后去逐步修整,那就是拆数组,递归拆数组.对半拆,然后拆出来的数据传再对半拆,拆成4个等分,然后再拆成8个,如此往复.最后一步一步的修整数组.
首先我们将特殊案例的代码我们封装一个函数Merge,后面会用到:
*******************************************************************************
Function Merge(大数组, 头子, 切割点, 尾巴)
Rem 大数组是需要排序的数组
Rem 起点是数组的下标,终点是数组的上标,中间值就是我们拆分数组的拆分线位置
Dim 临时数组
i = 头子
j = 切割点 + 1
k = 头子
Rem 左边较小的时候左边拿出一个数字放到大数组里面.左_i和大_i各递推一下,右数组也一样
Rem 但是当左或右数组的数字被拿完了的时候就直接复制结果到后面,也就是左_i或者右_i递推等于 _
左或右数组上标的时候就直接复制剩余结果
ReDim 临时数组(头子 To 尾巴)
While i <= 切割点 And j <= 尾巴
If 大数组(i) >= 大数组(j) Then
临时数组(k) = 大数组(i)
k = k + 1 '改变位置的数据位置各自递推一个
i = i + 1
Else
临时数组(k) = 大数组(j)
k = k + 1
j = j + 1
End If
Wend
Rem 这里是复制粘贴后面的数据,前面左或者右数组已经完成了对比
While i <= 切割点
临时数组(k) = 大数组(i)
k = k + 1
i = i + 1
Wend
While j <= 尾巴
临时数组(k) = 大数组(j)
k = k + 1
j = j + 1
Wend
For i = 头子 To 尾巴
大数组(i) = 临时数组(i)
Next
End Function
*******************************************************************************
这是一个函数,函数用法是
Merge(大数组, 头子, 切割点, 尾巴),函数有四个参数,
第一参数:一个需要排序的数组
第二参数:数组中特殊案例的部分的起始索引
第三参数:锯开数据串的位置数组索引,这个参数在递归中直接引用变量表示,看代码
第四参数:数组中特殊案例的部分的终止索引
我们再次引入一个数组来观察: 5 3 9 8 2 4 1 6
先设计一下递归的过程:
Sub 递归设计思路(数组,起始点,结束点)
语句1:设定退出语句,避免栈溢出(递归中永远要将这一句作为一个首要任务,不一定要放在第一句,但是一定最重要)
语句2:求出切割点,切割点 = (起始点+结束点)\2(反斜杠意思就是取整)
语句3:递归开始.直接引用自己: Call 递归设计思路(数组, 起始点,切割点),注意在这里,数据串已经分成了两半,那么前半部分的结束点就应该是切割点,而后半部分的起始点确是切割点.所以在后部分,还需要再次递归一次
语句4:再次递归, Call 递归设计思路(数组,切割点,结束点)
语句5:引用Merge函数, Merge 数组,起始点,切割点,结束点.
End sub
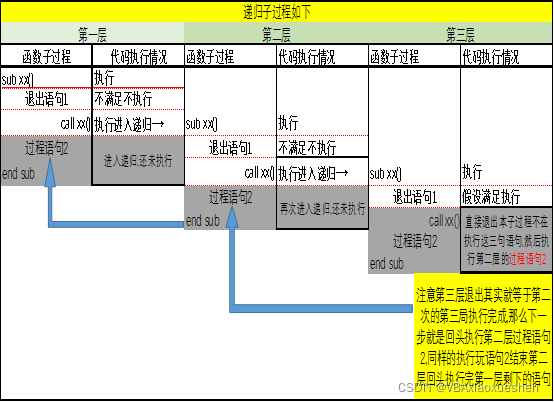
此时我建议再回头看看递归的演示图,对比上面的子过程,就不难看懂递归的整个过程了,我将演示图再次贴出
我们发现,在函数引用函数自己结束以前,你会发现,后面的语句压根不会执行,就像前面的小和尚一开始不睡觉一样,需要一位女施主的到来所有的小和尚才会按顺序去睡觉,上图的”过程语句2”其实就是这样,他会聚集到最后一步一层一层倒着执行回来.这一点很重要.此时我们再观察一下” 递归设计思路”这个子过程,你会发现,一开始语句5是不会执行的.他需要从倒数第二层开始一层一层的往回来.为什么我们要将他放在函数调用自己的语句的后面而不是前面?看图
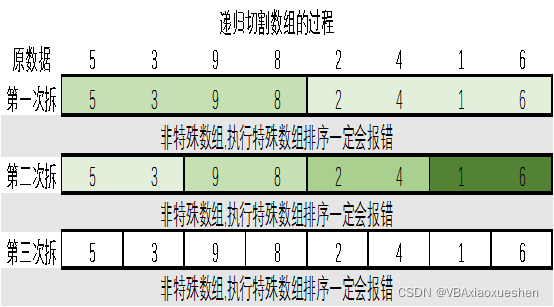
数组: 5 3 9 8 2 4 1 6的排序
原因就在这里,如果放在递归过程(函数)调用自己的语句之前,一定会处bug.(不是报错,制图失误)
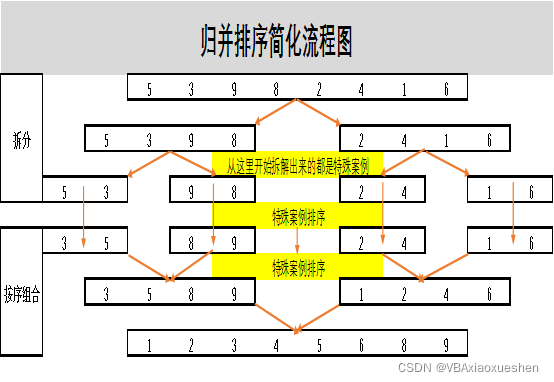
我们来看看为什么放在递归过程(函数)调用自己的语句之后就是正确的.放在递归过程(函数)调用自己的语句之后,执行特殊案例排序是在拆完数组以后,倒着执行回来的,看图
我们再来总结一下递归的前后过程,先将数组对半拆,递归再四分拆,递归再八分拆直至递归最后一层退出得到了多个被拆解成一对一对的数据串,每一对数据串都类似特殊案例,然后倒数第二层剩余的语句执行,也就是倒数第二层的Merge函数开始执行,调整每一对数据串,如此每一层都能调整数据使数组更接近于特殊案例,最后就可完成排序.
其实拆分相当于”老和尚讲故事”而特殊案例排序相当于”小和尚去睡觉”.归并排序并没有我们想象的那么难.
下面是归并排序的子过程,配合Merge函数可以实现一维数组的排序
*******************************************************************************
Function 归并排序(大数组, 头子, 尾巴)
If 尾巴 > 头子 Then
切割点 = Int((头子 + 尾巴) / 2)
归并排序 大数组, 头子, 切割点
Rem 当切割点一直递减到0的时候if不执行
Rem 注意这里参数的变化,上面这一句是左边数组拆分,下面一句是右边的数组拆分
归并排序 大数组, 切割点 + 1, 尾巴
Rem 注意这里,这一句累计起来,每一次递归都会累计一次,每一次都会砍一个中间值出来
Merge 大数组, 头子, 切割点, 尾巴
End If
归并排序 = 大数组
End Function
_______________________________________________________________________________
Sub 实验()
arr = Array(10, 22, 32, 1, 12, 18, 30, 45, 22, 30, 30, 80, 55, 96, 69, 46, 49, 92, 42, 71, 2, 3, 14, 15, 10, 0, 100)
brr = 归并排序(arr, 0, UBound(arr))
For i = 0 To UBound(arr)
Debug.Print arr(i)
Next
End Sub
*******************************************************************************
下面是多列归并排序且能自由升降的函数:
用法参看测试代码,也在下面
*******************************************************************************
Function 归并切割升序(大数组, 起点, 终点)
If 终点 > 起点 Then
切割点 = Int((起点 + 终点) / 2)
归并切割升序 大数组, 起点, 切割点
归并切割升序 大数组, 切割点 + 1, 终点
小区域排序升序 大数组, 起点, 切割点, 终点
End If
归并切割升序 = 大数组
End Function
Function 小区域排序升序(大数组, 起点, 切割点, 终点)
Dim 临时数组
i = 起点
j = 切割点 + 1
k = 起点
ReDim 临时数组(起点 To 终点)
While i <= 切割点 And j <= 终点
If 大数组(i) <= 大数组(j) Then
临时数组(k) = 大数组(i)
k = k + 1
i = i + 1
Else
临时数组(k) = 大数组(j)
k = k + 1
j = j + 1
End If
Wend
While i <= 切割点
临时数组(k) = 大数组(i)
k = k + 1
i = i + 1
Wend
While j <= 终点
临时数组(k) = 大数组(j)
k = k + 1
j = j + 1
Wend
For i = 起点 To 终点
大数组(i) = 临时数组(i)
Next
End Function
Function 归并切割降序(大数组, 起点, 终点)
If 终点 > 起点 Then
切割点 = Int((起点 + 终点) / 2)
归并切割降序 大数组, 起点, 切割点
归并切割降序 大数组, 切割点 + 1, 终点
小区域排序降序 大数组, 起点, 切割点, 终点
End If
归并切割降序 = 大数组
End Function
Function 小区域排序降序(大数组, 起点, 切割点, 终点)
Dim 临时数组
i = 起点
j = 切割点 + 1
k = 起点
ReDim 临时数组(起点 To 终点)
While i <= 切割点 And j <= 终点
If 大数组(i) >= 大数组(j) Then
临时数组(k) = 大数组(i)
k = k + 1
i = i + 1
Else
临时数组(k) = 大数组(j)
k = k + 1
j = j + 1
End If
Wend
While i <= 切割点
临时数组(k) = 大数组(i)
k = k + 1
i = i + 1
Wend
While j <= 终点
临时数组(k) = 大数组(j)
k = k + 1
j = j + 1
Wend
For i = 起点 To 终点
大数组(i) = 临时数组(i)
Next
End Function
Private Function 行号记录字典(All, 值列, 数组索引起点, 数组索引终点, Optional 功能 = 0)
Dim dic '创建字典,采用引用法
Set dic = CreateObject("Scripting.Dictionary")
'Dim Dic As New Dictionary '(勾选引用法)
For i = 数组索引起点 To 数组索引终点
Key = All(i, 值列)
If dic.Exists(Key) = False Then
Rem 不存在key的时候item就等于i,避免下面的 xxx & xxx 录入一个空值
dic(Key) = i
Else
dic(Key) = dic(Key) & "=*=" & i
End If
Next
Rem 根据功能选择输出
If 功能 = 0 Then
行号记录字典 = dic.keys '输出字典
ElseIf 功能 = 1 Then
行号记录字典 = dic.Items '输出值列
Else
Set 行号记录字典 = dic '输出关键字列
End If
End FunctionPrivate Function 单列归并排序模块(arr, 值列, 起点, 终点)
Dim 升降 As Boolean
If 值列 < 0 Then
值列 = Abs(值列)
升降 = False
ElseIf 值列 > 0 Then
值列 = Abs(值列)
升降 = True
End If
ReDim arr_son(起点 To 终点, LBound(arr, 2) To UBound(arr, 2))
Set dic = 行号记录字典(arr, 值列, 起点, 终点, 3)
arr_rows = dic.keys
If 升降 = True Then
arr_rows = 归并切割升序(arr_rows, LBound(arr_rows), UBound(arr_rows))
Else
arr_rows = 归并切割降序(arr_rows, LBound(arr_rows), UBound(arr_rows))
End If
ReDim brr(LBound(arr_rows) To UBound(arr_rows))
For i = LBound(arr_rows) To UBound(arr_rows)
brr(i) = dic(arr_rows(i))
Next
g = 起点
For i = LBound(brr) To UBound(brr)
crr = Split(brr(i), "=*=")
For t = LBound(crr) To UBound(crr)
For h = LBound(arr, 2) To UBound(arr, 2)
arr_son(g, h) = arr(Abs(crr(t)), h)
Next
g = g + 1
Next
Next
For i = 起点 To 终点
For t = LBound(arr, 2) To UBound(arr, 2)
arr(i, t) = arr_son(i, t)
Next
Next
End Function
Private Function 多列归并排序模块(arr, 值列串, 起点, 终点, Optional 递推 = 0)
arr_值组 = Split(值列串, ",")
s = UBound(arr_值组)
If 递推 > s Then Exit Function
If 递推 > 8 Then Exit Function
单列归并排序模块 arr, Val(arr_值组(递推)), 起点, 终点
brr = 行号记录字典(arr, Abs(arr_值组(递推)), 起点, 终点, 1)
For t = LBound(brr) To UBound(brr)
crr = Split(brr(t), "=*=")
If UBound(crr) > 0 Then
多列归并排序模块 arr, 值列串, crr(LBound(crr)), crr(UBound(crr)), 递推 + 1
End If
Next
End Function
以下为测试代码
Sub 多列归并测试()
arr = Sheet6.Range("a1:g52")
多列归并排序模块 arr, "+4,-5,+6,-7", 3, 52
Sheet6.Range("i1").Resize(52, 7) = arr
End Sub
*******************************************************************************
用法:
所有代码复制到excel的模块中
引用函数”多列归并排序模块”
多列归并排序模块(arr, 值列串, 起点, 终点, Optional 递推 = 0)
有五个参数,第五个参数不需要赋值,否则会出bug
第一参数:需要排序的数组
第二参数:排序的主次列,以"+4,-5,+6,-7"的形式输入,详细使用案例参看测试代码,其中”+”代表升序”-”代表降序,”+4,-5”的意思是主列4列升序次列5列降序
第三参数:数组需要排序的起始行
第四参数:数组需要排序的终止行
使用案例:测试代码
Sub 多列归并测试()
arr = Sheet6.Range("a1:g52")
多列归并排序模块 arr, "+4,-5,+6,-7", 3, 52
Sheet6.Range("i1").Resize(52, 7) = arr
End Sub
实验数据如下:
结果如下“: