LeetCode刷题复盘笔记—单调栈 739. 每日温度

今日主要总结一下，LeetCode 739. 每日温度(单调栈 )

题目：LeetCode 739. 每日温度(单调栈 )

Leetcode题目地址

题目描述：
给定一个链表，返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

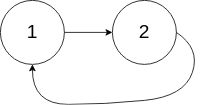
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引

进阶：是否可以使用 O(1) 空间解决此题？

一、哈希表

这道题比较容易想到的就是使用哈希表把所有节点都存下，之后一旦在哈希表里面找到相同的节点，就代表已经在环里面绕了一圈了，即入口节点

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        unordered_set<ListNode *> visited;
        while(head){
            if(visited.find(head) != visited.end()){
                return head;
            }
            visited.insert(head);
            head = head -> next;
        }
        return NULL;    
    }
};

本题重难点

重难点主要是这个 进阶：是否可以使用 O(1) 空间解决此题？
如果面试时遇到这个题，在给出哈希表解法时，面试官大概率会继续问有没有更好的方法？

二、快慢指针

原理：

我们使用两个指针，fast 与slow。它们起始都位于链表的头部。随后，slow 指针每次向后移动一个位置，而 fast 指针向后移动两个位置。如果链表中存在环，则fast 指针最终将再次与slow 指针在环中相遇。
如图所示，设链表中环外部分的长度为 a。slow 指针进入环后，又走了 b的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈，因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc
根据题意，任意时刻fast 指针走过的距离都为slow 指针的 2 倍。因此，我们有等式
a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)
有了 a=c+(n-1)(b+c)的等量关系，我们会发现：从相遇点到入环点的距离加上 n-1圈的环长，恰好等于从链表头部到入环点的距离
因此，当发现slow 与 fast 相遇时，我们再额外使用一个指针ptr。起始，它指向链表头部；随后，它和slow每次向后移动一个位置。最终，它们会在入环点相遇。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast = head;
        ListNode *slow = head;
        while(fast != NULL){
            slow = slow -> next;
            if(fast -> next == NULL){
                return NULL;
            }
            fast = fast -> next -> next;
            if(fast == slow){
                ListNode * pcur = head;
                while(pcur != slow){
                    pcur = pcur -> next;
                    slow = slow -> next;
                }
                return pcur;
            }
        }
        return NULL;
    }
};

复杂度分析

时间复杂度：O(N)，其中 N 为链表中节点的数目。在最初判断快慢指针是否相遇时，slow 指针走过的距离不会超过链表的总长度；随后寻找入环点时，走过的距离也不会超过链表的总长度。因此，总的执行时间为 O(N)+O(N)=O(N)

空间复杂度：O(1)。我们只使用了slow,fast,ptr 三个指针。

总结

C++中rand() 函数的用法函数

一、rand()不须要参数，它会返回一个从0到最大随机数的任意整数，最大随机数的大小一般是固定的一个大整数。spa

二、若是你要产生0~99这100个整数中的一个随机整数，能够表达为：int num = rand() % 100; 调试

 这样，num的值就是一个0~99中的一个随机数了。code

三、若是要产生1~100，则是这样：int num = rand() % 100 + 1; class

四、总结来讲，能够表示为：int num = rand() % n +a;随机数

 其中的a是起始值，n-1+a是终止值，n是整数的范围。程序

五、通常性：rand() % (b-a+1)+ a ; 就表示 a~b 之间的一个随机整数。im

六、若要产生0_{1之间的小数，则能够先取得0}10的整数，而后均除以10便可获得“随机到十分位”的10个随机小数。总结

 若要获得“随机到百分位”的随机小数，则须要先获得0~100的10个整数，而后均除以100，其它状况依 此类推。文件

七、一般rand()产生的随机数在每次运行的时候都是与上一次相同的，这样是为了便于程序的调试。

 若要产生每次不一样的随机数，则可使用srand( seed )函数进行产生随机化种子，随着seed的不一样，就可以产生        不一样的随机数。

八、还能够包含time.h头文件，而后使用srand(time(0))来使用当前时间使随机数发生器随机化，这样就能够保证每两 次运行时能够获得不一样的随机数序列，同时这要求程序的两次运行的间隔超过1秒。

九、举例以下：

rand（产生随机数）
表头文件: #include
定义函数 :int rand(void)

函数说明 :
由于rand() 的内部实现是用线性同余法作的，它不是真的随机数，只不过是由于其周期特别长，因此有必定的范围里可当作是随机的，
rand() 会返回一随机数值，范围在 0 至 RAND_MAX 间。
在调用此函数产生随机数前，必须先利用 srand()设置好随机数种子，若是未设随机数种子，rand()在调用时会自动设随机数种子为 1。
rand()产生的是假随机数字，每次执行时是相同的。若要不一样,以不一样的值来初始化它.初始化的函数就是 srand()。

返回值:
返回 0 至 RAND_MAX 之间的随机整数值，RAND_MAX 的范围最少是在 32767 之间（int），即双字节（16位数）。
若用unsigned int 双字节是 65535，四字节是 4294967295 的整数范围。
0~RAND_MAX 每一个数字被选中的机率是相同的。

---

欢迎大家关注本人公众号：编程复盘与思考随笔