基于流模型 Flow-based model 的图像缺陷检测算法

<2023.07.02> 新增 4.5 PyramidFlow 模型图和创新点总结
<2023.06.14> 新增 4.5 PyramidFlow 基础信息
<2023.05.01> 新增 4.4 FastFlow
<2023.04.24> 新增 4.3 CS-Flow
<2023.02.26> 新增 4.2 CFlow
<2023.02.26> 新增 4.3 DifferNet 的消融实验分析部分

本文介绍基于流模型的图像缺陷检测算法。其将 Normalizing Flow 与缺陷检测相结合，相关的几篇工作在近两年的缺陷检测工作中都取得了不错的成绩。

1 缺陷检测 Defect Detection

本文介绍的方法属于基于深度视觉模型的缺陷检测（Defect Detection）方法，这类方法旨在检测工业生产图像的异常。Fig.1 为MVTecAD 数据集部分数据可视化，绿框图像为正常图像，第二行红框图像为存在缺陷的图像而第三行图像为第二行对应图像的缺陷放大图。

Fig.1 MVTecAD

在工业检测领域，异常的图像是十分稀少的。因为缺陷的多样性难以全部采集以及缺陷存在稀疏性，无论是发生的频率还是在图像中缺陷所占据的面积，因此当前缺陷检测的主流论文更多是仅使用正常图像来进行模型的训练。

而从检测的粒度来看，大体分为图像级别，区域级别以及像素级别检测。

• 图像级别：检测出当前图像是否存在缺陷；
• 区域级别：检测出图像中的存在缺陷的大体区域；
• 像素级别：检测出图像中为缺陷的像素（类似分割图结果）；

2 Normalizing Flows

在介绍 Normalizing Flows 之前，我们先回顾下相关的数学知识，雅可比矩阵、行列式以及可逆函数的概念。

2.1 雅可比矩阵 Jacobian Matrix

给定函数 $f:{\mathbb{R}}^n\mapsto {\mathbb{R}}^m$ ，其将 $n$ 维向量 $x$ 转化为 $m$ 维的向量 $y$。 函数 $f$ 的一阶偏导数的排列为雅可比矩阵

J = [ ∂ f 1 ∂ x 1 ∂ f 1 ∂ x 2 ⋯ ∂ f 1 ∂ x n ∂ f 2 ∂ x 1 ∂ f 2 ∂ x 2 ⋯ ∂ f 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ f m ∂ x 1 ∂ f m ∂ x 2 ⋯ ∂ f m ∂ x n ] \mathbf{J} = \begin{bmatrix} {\frac{\partial f_1}{\partial x_1}}&{\frac{\partial f_1}{\partial x_2}}&{\cdots}&{\frac{\partial f_1}{\partial x_n}}\\ {\frac{\partial f_2}{\partial x_1}}&{\frac{\partial f_2}{\partial x_2}}&{\cdots}&{\frac{\partial f_2}{\partial x_n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {\frac{\partial f_m}{\partial x_1}}&{\frac{\partial f_m}{\partial x_2}}&{\cdots}&{\frac{\partial f_m}{\partial x_n}}\\ \end{bmatrix} J= ​∂x1​∂f1​​∂x1​∂f2​​⋮∂x1​∂fm​​​∂x2​∂f1​​∂x2​∂f2​​⋮∂x2​∂fm​​​⋯⋯⋱⋯​∂xn​∂f1​​∂xn​∂f2​​⋮∂xn​∂fm​​​ ​

2.2 行列式 Determinant

给定 $n\times n$ 矩阵 $M$ ，其行列式如下

d e t M = d e t [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] = ∑ j 1 j 2 ⋯ j n ( − 1 ) τ ( j 1 j 2 ⋯ j n ) a 1 j 1 a 2 j 2 ⋯ a n j n \mathsf{det} M = \mathsf{det} \begin{bmatrix} {a_{11}}&{a_{12}}&{\cdots}&{a_{1n}}\\ {a_{21}}&{a_{22}}&{\cdots}&{a_{2n}}\\ {\vdots}&{\vdots}&{\ddots}&{\vdots}\\ {a_{n1}}&{a_{n2}}&{\cdots}&{a_{nn}}\\ \end{bmatrix} = \sum_{j_1j_2\cdots j_n}^{} (-1)^{\tau(j_1j_2\cdots j_n)}a_{1j_1}a_{2j_2}\cdots a_{nj_n} detM=det ​a11​a21​⋮an1​​a12​a22​⋮an2​​⋯⋯⋱⋯​a1n​a2n​⋮ann​​ ​=j1​j2​⋯jn​∑​(−1)τ(j1​j2​⋯jn​)a1j1​​a2j2​​⋯anjn​​
其中该式子对下标 $j_1{j}_2\cdots j_n$ 关于 $\{1,2,\cdots ,n\}$ 的所有排列组合进行求和，$\tau (\cdot )$ 用于表示对应排列的符号。

若 $\det \mathbf{J}\ne 0$， 则该函数可逆。即 $y=f(x)$ 且 $x=f^{-1}(y)$。

2.3 变量变换理论 Change of Variable Theorem

若变量 $z$ 符合正态分布， $z\sim \pi (z)$ ，$x=f(z)$ ，且函数 $f$ 可逆，$z=f^{-1}(x)$。则有

$$\int p(x)dx=\int \pi (z)dz$$
上诉式子两端同时对 $x$ 求导，

$$p(x)=\pi (z)|\frac{dz}{dx}|=\pi (f^{-1}(x))|(f^{-1}{)}^{\prime }(x)|$$
上诉式子将求解 $x$ 的概率分布问题变成了求解 $z$ 的概率分布问题。

通过上诉方法，我们可以将难以求解的变量分布转化为易于求解的概率分布来进行计算。

2.4 应用：基于流模型的图像生成模型

对于图像生成模型而言，难点之一在于衡量生成图像 $x$ 是否逼真，也就是计算其是否为真实样本的概率 $p(x)$。

GAN 模型额外训练了判别器用于计算该概率，旨在判别生成图像是否逼真。而一些工作基于上诉 change of variable theorem 提出了基于流模型的生成方法。这类方法旨在构建正态分布隐变量 $z$ 到图像 $x$ 的可逆映射 $f$，以更方便的计算 $P(x)$。

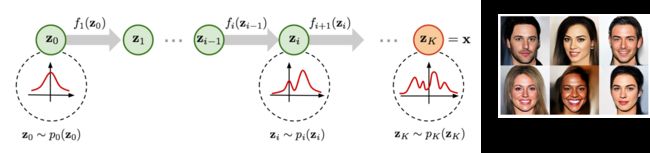
而在实际构建流模型的时候，为了生成分布更加复杂的图像集合，我们通常将多个可逆函数进行串联，如 Fig.2 所示。

Fig.2 Normalizing Flow

由此我们生成模型的优化任务变成了

$$\max p(x)=\pi (f^{-1}(x))|(f^{-1}{)}^{\prime }(x)|$$
即
$$\max \log p(x)=\log \pi (f^{-1}(x))-\log |\det \frac{df(x)}{dx}|$$

3 缺陷检测与流模型的关联

回过头来思考缺陷检测的问题范式，其与生成模型有一点相似，就是都需要去度量 $p(x)$。而近来也出现一些工作将流模型引入缺陷检测，旨在用流模型度量 $p(x)$。这个想法从原理上思考非常自然，简洁。

4 基于流模型的图像缺陷检测算法

4.1 DifferNet

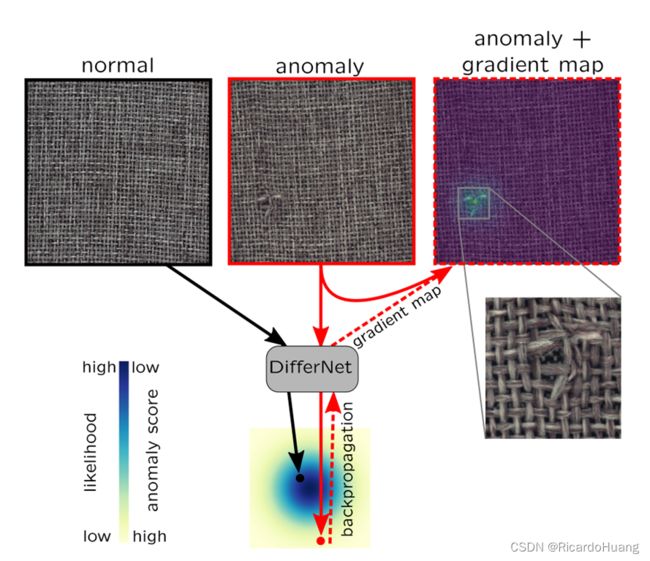
DifferNet 希望构建工业检测图像与正态分布隐变量的可逆映射，因此通过隐空间变量的似然估计来评估图像的异常值。同时其使用梯度图（gradient map）来进行缺陷定位（location）。

Fig.3 DifferNet 思路

如 Fig.4 所示，DifferNet 对图像进行了变换以及缩放，同时使用了特征提取器将图像变换为特征之后，再投影到正态分布空间。

Fig.4 DifferNet 详细流程

而如 Fig.5 所示为其使用的 normalizing flow 模块，其使用了 fc 全连接层组成映射函数。但对于图像数据来说 fc 捕捉不到其相关的位置信息，这估计会是其阻碍性能的一个问题。

Fig.5 Normalizing Flow Block in DifferNet

而对于缺陷定位部分，DifferNet 使用了各个通道的梯度图进行叠加来进行衡量。

$$g_x=\sum _{c\in C}|G\ast \nabla x_c|$$
其中 $C$ 代表通道数，而 $G$ 代表高斯核。

Fig.6 DifferNet 消融实验

对于 DifferNet 消融实验来说，其使用了 transf. 依旧是数据变换增广。而 train transf. 的作用与 # test transf. 不同，train transf. 为的是在训练时候进行数据增广，而 test tansf. 则是在测试的时候对同一张图像进行不同的变换（表格中的 1 表示没有变换，只有原图，而 4 表示除了原图之外有 $3=4-1$ 个变换），从根据不同的“视角”对图像进行检测，综合不同的”视角“图像的结果进行综合评测。test transf. 基于一个前提：异常图像经过变换之后仍然是异常图像，正常图像进行变换之后仍然是正常图像。语义层面上的异常语义不变。

不过这边不由思考是否有对其他方法使用这种方法，不然有失公平。且本文对比的方法都是比较久的方法，没有与其他的新方法进行对比；包括其像素级别的检测也是没进行量化分析，性能还是有限。但考虑到也是 Flow-based model 在异常检测领域的前几篇应用，算是开坑之作？（这边如果有误请指正），也算情有可原。而相应的一些问题，作者也在下一个工作 CSFlow 上进行了改进，之后继续细读分享。

4.2 CFlow-AD

Fig.7 Overview of CFLOW-AD

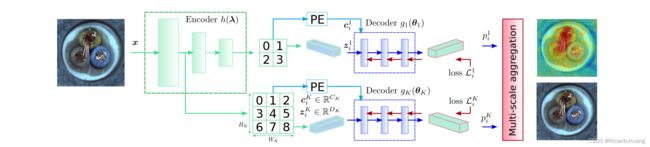
Fig.7 为 CFlow 的结构图。

与4.2所提的 DifferNet 不同，其在特征（图中为 Encoder）提取模块使用的为 CNN 模型 $h(\lambda )$ ，相较全连接层（FC layer）来说，CNN 模型能更好得捕捉到图像的局部空间结构信息，提取到更合适的特征。而且关于 CNN 的预训练模型已经有许多可供使用，论文中使用CNN模型是在 ImageNet 上预训练的，能更加有效得提取图像特征。

而对于不同尺寸的异常检测（图像级别的异常检测以及像素级别的异常检测），CFlow 分别使用网络的最后一层以及网络的第一层特征作为流模型的输入进行对应任务的检测。最后一层网络捕捉到全局信息，分辨率低，更有助于粗粒度的判别，而第一层网络捕捉到网络的局部信息，分辨率高，有助于局部细粒度分析。

4.3 CS-Flow

Fig.8 Overview of CS-FLOW

CS-Flow 论文：Fully Convolutional Cross-Scale-Flows for Image-based Defect Detection

CS-Flow 是 DifferNet 作者 Marco Rudolph 在之后提出的新方法。相对于 DifferNet 而言，作者更多在特征提取和特征多尺度交互上进行了改进。

特征提取 由于异常检测数据集的规模较其他大数据集相比较小，因此有许多的工作会使用在大数据集（如ImageNet）预训练得到的模型进行特征提取，希望能够提取到更加具有泛化能力，更加鲁棒的特征。在此，CS-Flow 使用了预训练好的 EfficientNet-B5 模型作为特征提取器。

多尺度特征交互 在进行推理时，CS-Flow 会先对图像进行缩放得到不同尺寸的图像，再使用预训练模型对其进行特征。接下来，CS-Flow 在 NF block 中的第二次融合时对不同尺寸的特征进行交互，实现跨尺寸的特征融合。

4.4 FastFlow

FastFlow: Unsupervised Anomaly Detection and Localization via 2D Normalizing Flows

Fig.9 Overview of FastFLOW

与之前的工作相似，FastFlow 方法包括特征提取以及 Normalizing flow 两部分。

但于此 FastFlow 在特征提取方面进行了更多的探索，使用了 Vision Transformer 模型作为特征提取器来使用。

Fig.10

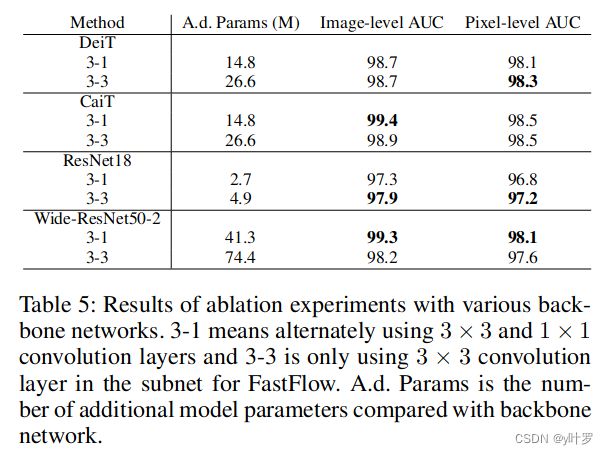
如图10所示为 FastFlow 在 backbone 方面进行的消融实验。相比其他的方法，FastFlow 对于图像缺陷检测常用预训练模型的使用探索是比较多的。包括其他的方法比如 PatchCore 之类的方法也有使用不同的预训练模型进行特征提取作为对比实验，个人认为可以当作是一个较不错的技术包括进行学习。

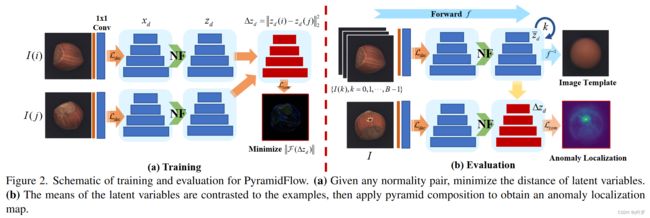
4.5 PyramidFlow

PyramidFlow: High-Resolution Defect Contrastive Localization using Pyramid Normalizing Flow

2023 CVPR 的一篇文章，作者来自浙江大学。

Fig.11 Overview of PyramidFLOW

与之前 NF 的方法不同，PyramidFlow 借鉴了模板匹配类型方法的思路，利用正常样本的 embedding 向量作为模板与测试样本进行匹配判断。其主要的创新点主要有3方面：

1. 使用了正常样本的 embedding 向量作为模板与测试样本进行匹配判断；
2. 使用了多尺度多样本的特征融合和映射；
3. 在不适用预训练模型的基础上取得了优于其他方法的结果。

参考 Reference

• Flow-based Deep Generative Models
• Same Same but DifferNet: Semi-Supervised Defect Detection With Normalizing Flows
• CFLOW-AD: Real-Time Unsupervised Anomaly Detection with Localization
  via Conditional Normalizing Flows
• Fully Convolutional Cross-Scale-Flows for Image-based Defect Detection
• FastFlow: Unsupervised Anomaly Detection and Localization via 2D Normalizing Flows
• PyramidFlow: High-Resolution Defect Contrastive Localization using Pyramid Normalizing Flow