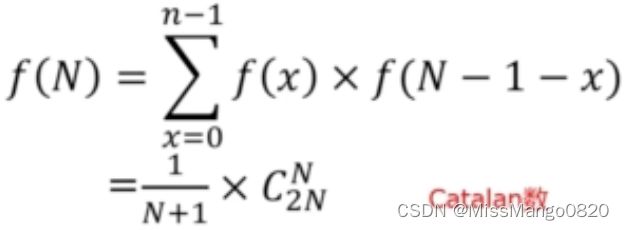数据结构与算法 | 第三章：栈与队列

本文参考网课为 数据结构与算法 ¹ 第三章栈，主讲人 张铭 、王腾蛟 、赵海燕 、宋国杰 、邹磊 、黄群。

本文使用IDE为 Clion，开发环境 C++14。

更新：2023 / 11 / 5

---

---

线性表 可以在表的任意位置进行元素的插入、删除等运算。而 栈（ Stack ）的运算只在表的一端进行，队列（ Queue ）的运算只在表的两端进行，因此可以将 栈 与 队列 视为操作受限的 线性表。

栈

概念

栈 是一种限制访问端口的 线性表，后进先出（ Last In First Out ）。
栈 的主要操作有 进栈（ push ）和 出栈（ pop ）。

栈 的应用有：

• 表达式求值
• 消除递归
• 深度优先搜索

栈 的抽象数据类型如下：

template <class T>
class stack{
public:                                 // 栈的运算集
    void clear();                       // 清空栈
    bool push(const T item);            // push item入栈。成功推入，返回真；否则返回假
    bool pop(T& item);                  // 返回栈顶内容并弹出。成功弹出，返回真；否则返回假
    bool top(T& item);                  // 返回栈顶但不弹出。成功弹出，返回真；否则返回假
    bool isEmpty();                     // 若栈已空，返回真
    bool isFull();                      // 若栈已满，返回真
};

示例

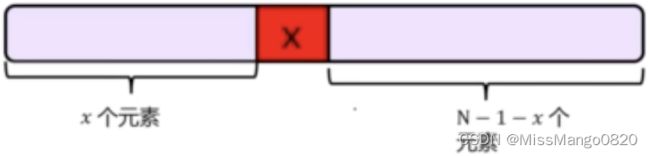
假如给定一个入栈顺序 1、2、3、4，则出栈的顺序可以有哪些？

设 k 是最后一个出栈的，那么 k 把序列一分为二。在 k 之前入栈的元素，一定在比在 k 之后入栈的元素要提前出栈。

假设已知出栈顺序为 1、4、2、3，3 是最后1个出栈的，那么 3 将 1、2、3、4 分为 1、2 和 4。即 1、2 的出栈要在 4 之前。然而 2 不可能早于 4 出栈，因此 1、4、2、3 是不可能的。

再假设出栈顺序为 1、3、4、2，2 是最后1个出栈的，那么 2 将 1、2、3、4 分为 1 和 3、4。显然，1 是在 3、4 之前的，3 也是可以在 4 之前的。

---

那么，现在给定一个入栈序列，序列长度为 N，请计算有多少种出栈序列。

设有 f(N) 个出栈序列，如果 x 是最后一个出栈的，那么 x 个元素一定在 N-1-x 个元素之前出栈。

前面的 x 个元素有 f(x) 种出栈序列，后面的 N-1-x 个元素有 f(N-1-x) 种出栈序列。x 和 N-1-x 个元素之间的整体出栈顺序是确定的，但是它们内部的出栈顺序是不定的，所以：

x 可以从 0 到 N-1。

实现

栈 的物理实现有2种，1种称为 顺序栈（ Array-based Stack ），另1种称为 链式栈（ Linked Stack ）。

顺序栈

使用向量实现，本质是 顺序表 的简化版。
关键是确定哪一端作为栈顶。

类定义

#include 
#include 
using namespace std;

template class <T> class arrStack:public Stack<T>{
private:                                                // 栈的顺序存储
    int mSize;                                          // 栈中最多可存放的元素个数
    int top;                                            // 栈顶位置，应小于mSize
    T *st;                                              // 存放栈元素的数组
public:
    arrStack(int size){                                 // 构造函数，创建一个给定长度的顺序栈实例
        mSize = size; top = -1; st = new T[mSize];
    }
    ~arrStack(){delete [] st;}                          // 析构函数
    void clear(){top = -1;}                             // 清空栈；将栈顶top指向栈底，过后，若有新的元素入栈则会覆盖栈内原有的元素
};

进出栈

进栈

当栈中已经有 maxsize 个元素时，如果再做进栈运算，会产生 上溢（ overflow ）。

因此，压入栈顶时需要做边界条件判定再进行入栈，如下：

bool arrStack<T>::push(const T item){
    if (top == mSize - 1){                  // 满栈
            count << "栈满溢出" << endl;
            return false;
    }else{                                  // 新元素入栈并修改栈顶指针
        st[++top] == item;					// top指针做自增
        return true;
    }
}

出栈

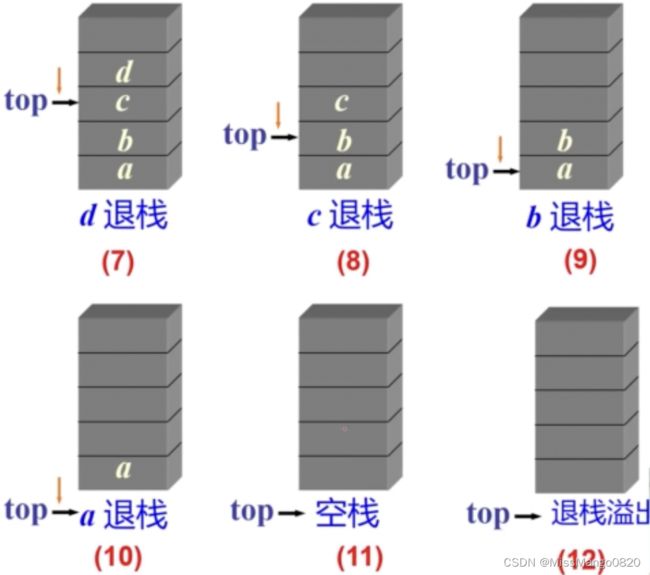
对 空栈 进行出栈运算时可能会出现 下溢（ underflow ）。

因此，弹出栈顶时需要做边界条件判定再进行出栈，如下：

bool arrStack<T>::pop(T& item){         // 出栈
    if (top == -1){                     // 空栈
        cout << "空栈，不能出栈" << endl;
        return false;
    }else{
        item = st[top--];               // 返回栈顶，并缩减1
        return true;
    }
}

链式栈

用 单链表 方式存储，其中指针的方向是从栈顶向下链接。

类定义

template <class T> class lnkStack: public Stack<T>{
private:                                                // 栈的链式存储
    Link<T>* top;                                       // 指向栈顶的指针
    int size;                                           // 存放元素的个数
public:                                                 // 栈运算的链式元素实现
    lnkStack(int defSize){                              // 构造函数
        top = NULL; size = 0;
    }
    ~lnkStack(){                                        // 析构函数
        clear();
    }
};

进出栈

进栈

bool lnkStack<T>::push(const T item){           // 入栈操作的链式实现
    Link<T>* tmp = new Link<T>(item, top);
    top = tmp;
    size ++;
    return true;
}
Link(const T info, Link* nextValue){            // 具有2个参数的Link构造函数
    data = info;
    next = nextValue;
}

出栈

bool lnkStack<T>::pop(T& item){
    Link <T> *tmp;
    if (size == 0){
        cout << "空栈，不能出栈" << endl;
        return false;
    }
    item = top -> data;                     // 将top的数据赋值给item，将item弹出去
    tmp = top -> next;                      // 将top的next指向tmp
    delete top;                             // delete top对应的内存空间
    top = tmp;                              // 将tmp对应的数据赋值给top
    size--;                                 // 元素数量自减1
    return true;
}

顺序栈 V.S 链式栈

• 时间效率

  • 所有操作都只需要常数时间。二者难分伯仲。

• 空间效率

  • 顺序栈 须说明一个固定的长度；
  • 链式栈 的长度可变，但是增加结构性开销；

• 应用范围

• 实际应用中，顺序栈 比 链式栈 应用范围更广泛

应用

栈 的特点是后进先出。

栈 通常被用来处理具有递归结构的数据：

• 深度优先搜索
• 表达式求值
• 子程序 / 函数调用的管理
• 消除递归

表达式求值

表达式的递归定义：

• 基本符号集
  { 0，1，…，9，+，-，*，/，(，) }
• 语法成分集
  { <表达式>，<项>，<因子>，<常数>，<数字> }
  • 表达式
    • 中缀表达式
      23 + （34*45）/ （5 + 6 + 7）
    • 后缀表达式
      23 34 45 * 5 6 + 7 + / +

中缀表达式

概念

中缀表达式 的特点是：

• 运算符在中间
• 需要括号来改变优先级

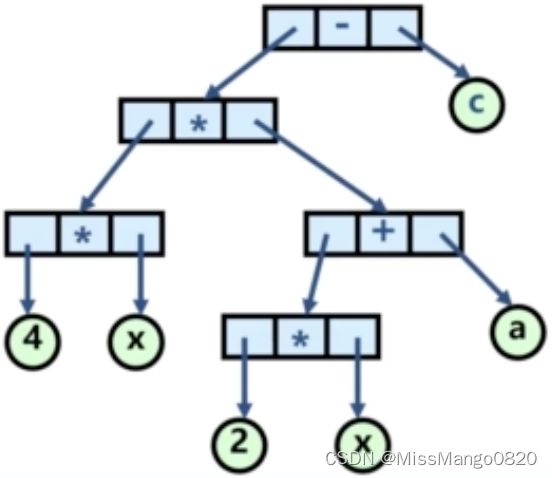
中缀表达式 可以使用树状结构表示，例如，以下面的树状结构表达 4 * x * ( 2 * x + a ) - c：


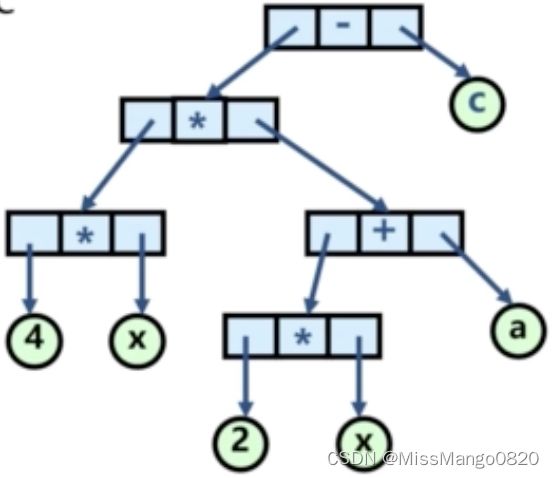
也可以使用语法公式表示，


也可以使用递归图示表示，

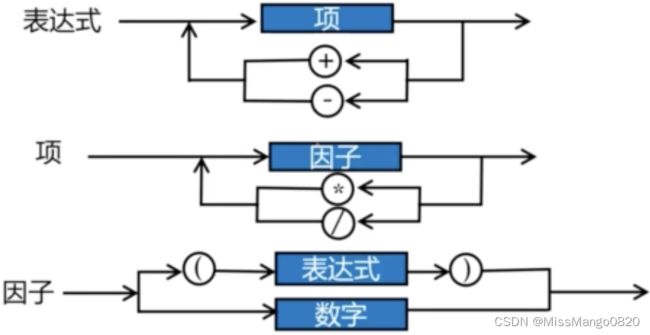
后缀表达式

概念

后缀表达式 的特点是：

• 运算符在后面
• 不需要括号

后缀表达式 可以使用树状结构表示，例如，以下面的树状结构表达 4x * 2x * a+ *c -：

示例

对后缀表达式求值

假设待处理后缀表达式为 34 45 * 5 6 + 7 + / +。

使用 栈 的概念对该后缀表达式进行求值的算法为：
依次顺序读入表达式的符号序列（假设以 = 作为输入序列的结束 ），并根据读入的元素符号逐一分析：

1. 当遇到的是一个操作数，则压入栈顶；
2. 当遇到的是一个运算符，则从栈中两次取出栈顶，按照运算符对这两个操作数进行计算。然后将计算结果压入栈顶。

如此继续，直到遇到符号 =，这时栈顶的值就是输入表达式的值。

以代码来表示上述算法思想，即：

class Calculator{
private:
    Stack<double> s;                                    // 这个栈用于压入、保存操作数
    bool GetTwoOperands(double& opd1, double& opd2);    // 操作1：从栈顶弹出两个操作数 opd1 和 opd2
    void Compute(char op);                              // 操作2：取两个操作数，并按op对两个操作数进行计算
public:
    Calculator(void){};                                 // 创建计算器实例，开辟一个空栈
    void Run(void);                                     // 读入后缀表达式，遇 "=" 符号结束
    void Clear(void);                                   // 清除计算器，为下一次计算做准备
};

template<class ELEM>
bool Calculator<ELEM>::GetTwoOperands(ELEM& opnd1, ELEM& opnd2){
    if (S.IsEmpty()){                                               // 空栈。则无法按预期取出2个操作数。
        cerr << "Missing Operand!" << endl;
        return false;
    }
    opnd1 = S.Pop();                                                // 取出右操作数
    if (S.IsEmpty()){                                               // 取出右操作数后，栈空，则无法取到左操作数。
        cerr << "Missing Operand!" << endl;
        return false;
    }
    opnd2 = S.Pop();                                                // 取出左操作数
    return true;
}

template <class ELEM> void Calculator<ELEM>::Compute(char op){
    bool result; ELEM operand1, operand2;
    result = GetTwoOperands(operand1, operand2);
    if (result == true)
        switch(op){
        case '+': S.Push(operand2 + operand1); break;
        case '-': S.Push(operand2 - operand1); break;
        case '*': S.Push(operand2 * operand1); break;
        case '/': if (operand1 == 0.0){
            cerr << "Divide by 0!" << endl;
            S.ClearStack();
            }else S.Push(operand2 / operand1);
            break;
        }
    else S.ClearStack();
}

template <class ELEM> void Calculator<ELEM>::Run(void){
    char c; ELEM newoperand;
    while (cin >> c, c!='='){
        switch(c){
        case '+': case '-': case '*': case '/':            // 如果碰到的是+-*/这种操作符，则调用compute运算
            Compute(c);
            break;
        default:                                           // 如果碰到的不是+-*/这种运算符，把c这种char类型数据放回栈内并再次读取newoperand这种ELEM
            cin.putback(c); cin >> newoperand;
            S.Push(newoperand);
            break;
        }
    }
    if (!S.IsEmpty())
        cout << S.Pop() << endl;                           // 打印出最后结果
}

中缀表达式转换为后缀表达式

对后缀表达式求值时，向栈内存操作数；

转换中缀表达式为后缀表达式时，向栈内存操作符。因为所有的操作数载顺序上并没有变化，但是操作符的顺序有变化。

• 当输入是操作数，直接输出到后缀表达式序列；
• 当输入是左括号时，直接压栈；
• 当输入是运算符时，
  • while
    • if (栈非空 and 栈顶不是左括号 and 输入运算符的优先级 <= 栈顶运算符的优先级) 时，将当前栈顶元素弹栈，输出到后缀表达式序列中；
      并将输入运算符压栈；
    • else 把输入的运算符压栈

输入运算符的优先级别<=栈顶运算符的优先级，比如输入运算符 +、栈顶运算符 *，则将栈顶 * 弹栈。

• 当输入是右括号时，先判断栈是否为空：
  • 若栈为空，即无任何左括号已在栈内，则清栈退出；
  • 若栈非空，则把栈中的元素依次弹出：
    • 遇到第一个左括号为止，将弹出的元素输出到后缀表达式的序列中（弹出的开括号不放到序列中）
    • 若未遇到开括号，说明括号不匹配，则清栈退出；
• 当中缀表达式的符号序列全部读入时，若栈内仍有元素，则把它们全部依次弹出，都放到后缀表达式序列尾部；
  • 若弹出的元素遇到开括号，说明括号不匹配，需要做错误异常处理。

递归

概念

递归、迭代

递归 和 迭代 的异同点：

• 相同点
  从小规模的相同问题来求解大规模问题
• 不同点
  • 迭代 先从小问题入手，然后自底向上组合成大问题
  • 递归 先从大问题入手，然后自顶向下，对大问题进行分解

递归 更接近人类思维方式。因此，涉及递归算法比设计非递归算法往往更容易，大多数编程语言支持递归，许多函数式编程语言更是直接以递归为基础。
递归 在完成问题定义时，基本也同时完成了问题求解。

递归函数

在计算机中，我们通常以函数的方式对递归问题进行定义与求解。所谓 递归函数，指的是会直接或间接调用自身的函数。
递归函数 具有2个要素：一是基本的边界情形（ 一般是规模小到不需要依赖子问题、可以直接求解的情形 ），二是递归规则（ 决定如何将一个递归问题转化为规模更小的子问题 ）。

计算机程序是一组顺序执行的指令序列。那么怎样用指令序列运行一个 递归函数 呢？
先看程序的内存分布，如下图：

内存被分为好几个区域，比如有内核、动态链接库、存放代码的只读区、存放全局变量的可读写区等等。
程序运行时，有两个区域的内存是不固定的：

• 栈
  主要用于函数调用
• 堆
  用于分配动态内存空间

递归函数 的相关操作主要发生在 栈 内。
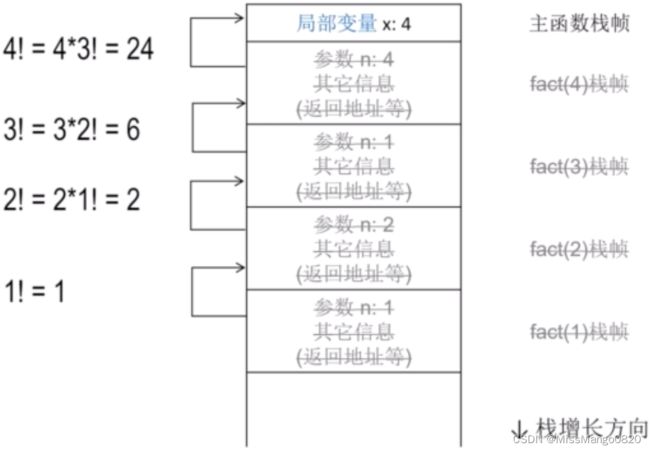
在函数调用栈里，元素是一种被称为栈帧的数据结构，每个帧对应1次函数调用，保存当次函数调用时传入的参数、函数返回地址以及局部变量。
比如，调用阶乘函数来求4的阶乘，如下：

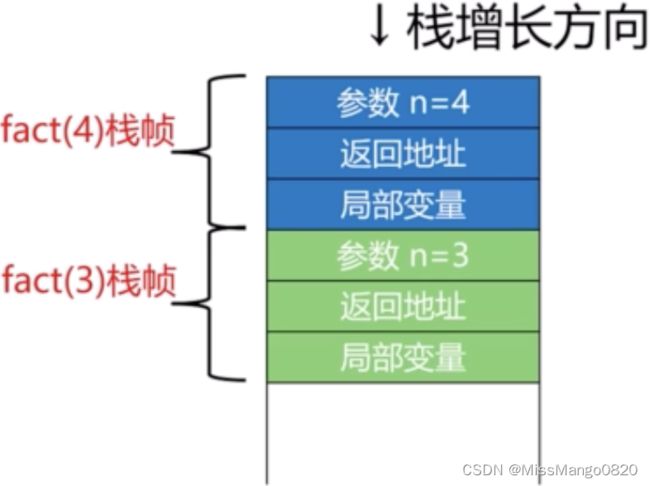
有一个阶乘4对应的帧；有一个阶乘3对应的帧。每个帧内保存了此次函数调用时的相关信息，比如传入的参数、函数的返回地址以及局部变量等。
计算机中的函数调用与退出主要就是对调用栈中的帧进行操作：

• 函数调用时
  • 计算机在栈中压入一个帧
    • 压入调用参数
    • 压入返回地址
    • 为局部变量分配空间
    • 其它信息（寄存器信息）
  • 计算机通过指令跳转到被调用函数开始的位置，开始执行
• 函数退出时
  • 记录返回值
  • 释放栈帧（局部变量、返回地址、调用函数及其它信息）
  • 根据返回地址，跳回调用前位置继续执行

递归函数 的运行时的空间、时间开销分析如下：

• 空间
  • 在每次调用时都需要创建栈帧并进行相应操作。在现实中，许多复杂函数的栈帧都很大，当调用次数很多时可能会把栈的空间全部用完，在一些系统上甚至可能会越界到动态链接库的区域，导致栈溢出的安全风险。
• 时间
  • 栈操作需要消耗计算资源
  • 函数调用与退出时的跳转指令相比于其他正常指令的开销也是较大的

因此，如果能将递归函数转换为非递归函数，就可以减少程序运行时的开销。

尾递归

尾递归 指的是函数仅有一次自身调用，且该调用时函数退出前的最后一个操作。

举例如下：

long fact(long n){
    if (n<=1)
        return 1;
    else
        return n * fact(n-1);
}

虽然上面的阶乘递归函数只有一次对自身的调用，但是该调用并不是退出前的最后一个操作。因为在调用之后，还有一个乘法操作。所以该递归阶乘并非尾递归。

long fact_tail_rec(long n, long product){
    if (n<=1)
        return product;
    else
        return fact_tail_rec(n-1, product * n)
}

上面的 尾递归 函数多了一个参数用来保存乘积，则原先的乘法结果可以以参数的形式在调用前进行传递，而不再需要在函数内进行乘法操作。这样，自身调用就时函数退出前的最后一个操作，因此，它是一个 尾递归 函数。

尾递归 可以很容易将 递归函数 转化为 非递归函数。尾递归 的本质是将单次计算的结果缓存起来以参数的形式传递给下一次调用，因此我们可以很容易地使用循环迭代的方式来保存这个累计的结果。

在 递归函数 转化为 非递归函数 之后，就可以消除栈开销与函数调用的开销。相比于原先线性增长的栈空间，转换之后只需要常数空间即可。

许多现代编程语言支持对 尾递归 的优化：

• 编译器/解释器
  GCC、LLVM / Clang、Intel 编译器、Java 虚拟机
• 函数式编程语言
  LISP、Scheme、Scala、Haskell、Erlang

示例

阶乘函数的调用栈

long fact(long n){
    if (n<1)
        return 1;
    else
        return n*fact(n-1);

    int main(){
        int x=4;
        printf("%d\n", fact(x));
        return 0;
    }
}

递归到非递归的转换

背景：假如有n件物品，物品i的重量为w[i]。如果限定每种物品，要么完全放进背包、要么不放进背包，即物品是不可分割的。

问题：能否从这n件物品中选择若干件放入背包，使其重量之和恰好为s。

通用的机械转换步骤

1. 定义栈帧，建立调用帧；
2. 在栈中压入原始问题的帧（ rd = 0 ）;
3. 根据递归调用数 t，将程序划分为 t+1 个区域；
4. 创建（t+2）个标签，逐区域翻译（除 return 语句、递归调用）;
   （ t+2 ）个标签为（t+1）个区域的边界
5. 用 goto 实现递归调用
   形式 “push stack；goto label 0”，第 i 个调用的 rd=i；
6. 用 goto 实现 return 语句；
   将所有 “return” 替换为 “goto label (t+1)”
7. 在标签 t+1 后添加递归出口
   使用 “switch” 语句，根据栈顶的 rd 值判断继续执行的标签

队列

概念

队列 是一种限制访问点的 线性表，先进先出（ First In First Out ）。

• 按照到达的顺序来释放元素；
• 所有的插入在表的一端进行，所有的删除都在表的另一端进行；

队列 的主要元素有 队头（ front ）、队尾（ rear ）。

队列 的主要操作：

• 入队列（ enQueue ）
• 出队列（ deQueue ）
• 取队首元素（ getFront ）
• 判断队列是否为空（ isEmpty ）

队列 的抽象数据类型如下：

template <class T> class Queue{
public:                                 // 队列的运算集
    void clear();                       // 清空队列
    bool enQueue(const T item);         // 将item插入队尾。成功则返回真，否则则返回假
    bool deQueue(T & item);             // 返回队头元素并将其从队列中删除，成功则返回真
    bool getFront(T & item);            // 返回队头元素，但不删除，成功则返回真
    bool isEmpty();                     // 返回真，若队列已空
    bool isFull();                      // 返回真，若队列已满
};

实现

队列 的物理实现有2种，1种称为 顺序队列（ Array-based Stack ），另1种称为 链式队列（ Linked Stack ）。

顺序队列

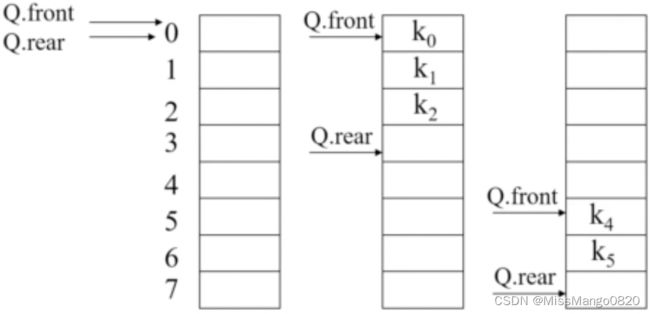
用 向量 存储队列元素，用两个变量分别指向队列的前端（ front ）和尾端（ rear ）。

• front：指向当前待出队的元素位置（地址）
• rear：指向当前待入队的元素位置（地址）

然而，这种 顺序队列 会有 溢出 的问题 ——

• 上溢
  当 队列 满时，再做进队操作
• 下溢
  当 队列 空时，再做删除操作
• 假溢出
  当 rear = mSize - 1 时，再作插入运算就会产出 溢出。如果这时 队列 的前端还有许多空位置，这种现象称为 假溢出

为了避免 溢出 的出现，可以将 顺序队列 的首尾相连来变成一个 循环队列。

类定义

class arrQueue:public Queue<T>{
private:
    int mSize;                          // 声明队列的数组大小
    int front;                          // 表示队头所在位置的下标
    int rear;                           // 表示待入队元素所在位置的下标
    T   *qu;                            // 存放类型为T的队列元素的数组
public:
    arrQueue(int size){                 // 创建队列的实例
        mSize = size + 1;               // 浪费一个存储空间，以此区别空队列和满队列
        qu = new T [mSize];
        front = rear = 0;
    }
    ~arrQueue(){                        // 消除该实例，并释放其空间
        delete[] qu;
    }
};

bool arrQueue<T>::enQueue(const T item){// item入队，插入队尾
    if (((rear + 1) % mSize == front)){ // rear指针+1，再对mSize取模，如果等于front，说明队列已满
        cout << "队列已满，溢出" << endl;
        return false;
    }
    qu[rear] = item;
    rear = (rear + 1)%mSize;            // 循环后继，将rear指针后移一位
    return true;
}

bool arrQueue<T>::deQueue(T& item){     // 返回队头元素并从队列中删除
    if (front == rear){                 // front指针等于rear指针，说明队列为空，不允许删除元素
        cout << "队列为空" << endl;
        return false;
    }
    item = qu[front];                   // item为队首元素
    front = (front + 1)%mSize;          // 循环后继，将front指针后移一位
    return true;
}

链式队列

链式队列 的本质是 单链表。用 单链表 方式存储，链接指针的方向是从队列的前端向尾端链接。

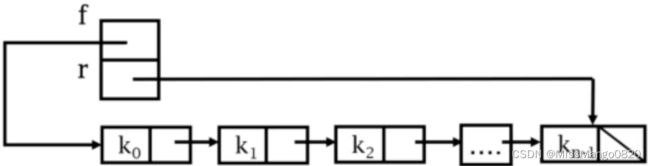
用 front 指向 单链表 的队首。用 rear 指针指向 单链表 的队尾。
我们把入队列和出队列限制在队首和队尾这两部分。不允许在其他部分进行操作。那么这其实就是一个 链式队列。

类定义

template <class T>
class lnkQueue:public Queue<T>{
private:
    int size;                                       // 队列中当前元素的个数
    Link<T>* front;                                 // 表示队头的指针
    Link<T>* rear;                                  // 表示队尾的指针
public:
    lnkQueue(int size);                             // 创建队列的实例
    ~lnkQueue();                                    // 消除该实例，并释放其空间
};

bool enQueue(const T item){                         // item入队，插入队尾
    if (rear == NULL){                              // 空队列
            front = rear = new Link<T>(item, NULL);
    }
    else{                                           // 添加新元素
        rear -> next = new Link<T>(item, NULL);     // rear的next指针指向新元素
        rear = rear -> next;                        // rear指针指向最后一个元素
    }
    size ++;
    return true;
}

bool deQueue(T* item){                              // 返回队头元素并从队列中删除
    Link<T> *tmp;
    if (size == 0){                                 // 队列为空，没有元素可出队
        cout << "队列为空" << endl;
        return false;
    }
    *item = front -> data;                          // 将front指针指向的队首元素传给item
    tmp = front;                                    // tmp指针记录front的位置
    front = front -> next;                          // 将front指针指向原队首的下一个元素
    delete tmp;                                     // 删除tmp
    if (front == NULL)                              // 如果front是空的，则rear也为空
        rear = NULL;
    size --;
    return true;
}

顺序队列 V.S 链式队列

• 空间效率
  • 顺序队列 需要固定的存储空间；
  • 链式队列 可以满足大小无法估计的情况；

应用

队列 满足先来先服务特性的应用，作为其数据组织方式或中间数据结构：

• 调度或缓冲
  • 消息缓冲器
  • 邮件缓冲器
  • 计算机硬设备之间的通信也需要队列作为数据缓冲
  • 操作系统的资源管理
• 宽度优先搜索

宽度优先搜索

示例：人狼羊菜过河

初步分析

• 问题抽象

“人狼羊菜” 乘船过河。只有人能撑船，船只有两个位置（包括人）。狼羊、羊菜不能在没有人时共处。

---

• 求解方案

求解该问题最简单的方法是使用试探法，即一步一步进行试探，每一步都搜索所有可能的选择，对前一步合适的选择再考虑下一步的各种方案。

用计算机实现上述求解的搜索过程可以采用两种不同的策略：

• 队列
  • 宽度优先搜索
    搜索该步的所有可能状态，再进一步考虑后面的各种情况
• 栈
  • 深度优先搜索
    沿某一状态走下去，不行再回头

假定采用宽度优先搜索解决农夫过河问题：

• 采用队列作辅助结构，把下一步所有可能达到的状态都放在队列中，然后顺序取出对其分别处理。
• 由于队列的操作按照先进先出原则，因此只有前一步的所有情况都处理完之后才能进入下一步。

先对数据进行抽象，对每个角色的位置进行描述。人、狼、羊和菜，四个目标依次各用一位，目标在起始岸位置 0、目标岸 1。
0110 表示农夫、白菜在起始岸，而狼、羊在目标岸。此状态为不安全状态。
1000 （ 0x08 ）表示人在目标岸，而狼、羊、菜在起始岸。
1111 （0x0F）表示人、狼、羊、菜都抵达目标岸。

如何从上述状态中得到每个角色所在位置？

bool farmer(int status)
{return ((status & 0x08) != 0);}

bool wolf(int status)
{return ((status & 0x04) != 0);}

bool goat(int status)
{return ((status & 0x02) != 0);}

bool cabbage(int status)
{return ((status & 0x01) != 0);}

函数返回值为真，表示所考察人或物在目标岸。否则，所考察人或物在起始岸；

在用以上方法拿到每个角色的所在位置之后可以对安全状态进行判断：

bool safe(int status)                   // 返回true 安全；返回false，不安全
{
    if ((goat(status) == cabbage(status)) && (goat(status) != farmer(status)))  // 羊和白菜共处，但是人不在
        return(false);
    if ((goat(status) == wolf(status) && (goat(status) != farmer(status))))     // 狼和羊共处，但是人不在
        return(false);
    return(true);
}

最终分析

• 问题抽象

从状态 0000（整数0）出发，寻找全部由安全状态构成的状态序列，以 1111（整数15）为最终目标。
状态序列中每个状态都可以从前一状态通过农夫（可以带一样东西）划船过河的动作到达。
序列中不能出现重复状态。

---

• 算法设计

定义一个整数队列 moveTo，它的每个元素表示一个可以安全到达的中间状态。
还需要定义一个数据结构记录已被访问过的各个状态，以及已被发现的能够到达当前这个状态的路径。

• 用 顺序表 route 的第i个元素记录状态i是否已被访问过
• 若route[i] 已被访问过，则在这个 顺序表 元素中记入前驱状态值，-1表示未被访问
• route的大小（长度）为16

---

• 算法实现

void solve(){
    int movers, i, location, newlocation;
    vector<int> route(END+1, -1);
    queue<int> moveTo;                              // 定义初始队列，看它moveTo到哪些队列上去
    moveTo.push(0x00);
    route[0]=0;
}

while (!moveTo.empty() && route[15] == -1){         //
    status = moveTo.front();                        // 拿到moveTo的front指针
    moveTo.pop();                                   // 把当前状态pop出来
    for (movers = 1; movers <= 8; movers << = 1){    // 农夫总是在移动。movers指针逐渐左移
        if (farmer(status)) == (bool)(status & movers){ // farmer(status)获取农夫状态，是1还是0;
                                                        // (status&movers)获取菜的状态，是1还是0；
                                                        // 如果农夫和菜的状态一致
            newstatus = status ^ (0x08 | movers);       // status ^ (0b1001 | 0b0001)，即status 和 0b1001作异或操作，得0b0110
            if (safe(newstatus) && (route[newstatus] == -1)){   // 调用safe判断status的下一个状态newstatus是否安全。如果newstatus不安全，则不能变；
                                                                // route[newstatus] == -1，说明newstatus未被访问过
                route[newstatus] = status;
                moveTo.push(newstatus);                         // 将newstatus计入moveTo队列
            }
        }
    }
    if (route[15] != -1){                                           // 如果最后一个状态0b1111对应的不是-1，说明最后一个状态已经达到
        cout << "The reverse path is:" << endl;
        for (int status = 15; status >= 0; status = route[status]){ // 从最后一个状态0b1111开始，
            cout << "The status is:" << status << endl;
            if (status == 0) break;
        }
    }
    else
        cout << "No solution." << endl;
}

---

参考链接

---

1. 数据结构与算法 ↩︎