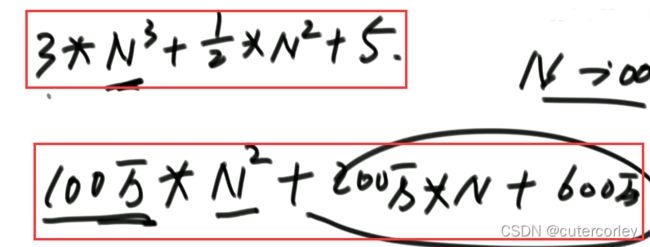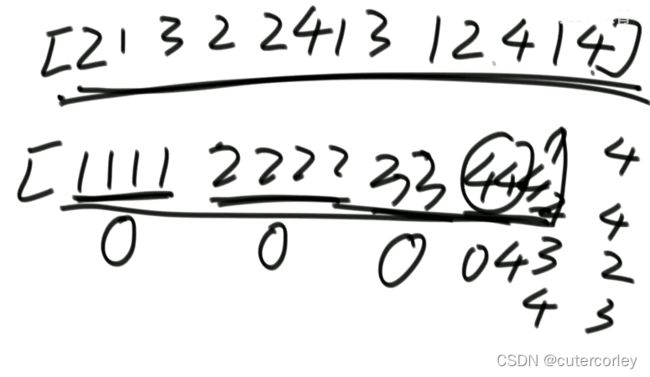算法与数据结构全阶班-左程云版(二)基础阶段之1.复杂度、对数器、二分法和异或运算
文章目录
- 引言
- 1.概述
- 2.复杂度
- 3.对数器
- 4.二分法
- 5.异或运算
- 总结
引言
本文主要介绍了数据结构与算法的基本概念,包括算法评价指标、复杂度、对数器、二分法和异或运算。
1.概述
评价算法优劣的核心指标
- 时间复杂度(流程决定)
- 额外空间复杂度(流程决定)
- 常数项时间(实现细节决定)
常见的常数时间的操作:
-
常见的算术运算(+、-、*、/、%等)
-
常见的位运算(>>、>>>、<<、|、&、^等)
-
赋值、比较、自增、自减操作等
-
数组寻址操作
总之,执行时间固定的操作都是常数时间的操作。
反之,执行时间不固定的操作,都不是常数时间的操作。
时间复杂度就是计算常数操作了多少次。
如何确定算法流程的总操作数量与样本数量之间的表达式关系:
- 想象该算法流程所处理的数据状况,要按照最差情况来。
- 把整个流程彻底拆分为一个个基本动作,保证每个动作都是常数时间的操作。
- 如果数据量为N,看看基本动作的数量和N是什么关系。
2.复杂度
如何确定算法流程的时间复杂度:
当完成了表达式的建立,只要把最高阶项留下即可。低阶项都去掉,高阶项的系数也去掉。
记为:O(忽略掉系数的高阶项)
例如下图:
显然后者的时间复杂度更低。
时间复杂度的意义在于:
当我们要处理的样本量很大很大时,我们会发现低阶项是什么不是最重要的;每一项的系数是什么,不是最重要的。真正重要的就是最高阶项是什么。
这就是时间复杂度的意义.它是衡量算法流程的复杂程度的一种指标,该指标只与数据量有关,与过程之外的优化无关。
三种基本排序:
选择排序:
package complexity01;
import java.util.Arrays;
/**
* @author Corley
* @date 2021/10/3 19:26
* @description LeetCodeAlgorithmZuo-complexity01
*/
public class SelectionSort {
public static void selectionSort(int[] arr) {
if (null == arr || arr.length < 2) {
return;
}
int minIndex;
for (int i = 0; i < arr.length - 1; i++) {
minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[minIndex] < arr[j] ? minIndex : j;
}
swap(arr, i, minIndex);
}
}
private static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void main(String[] args) {
int[] arr = new int[]{3, 2, 5, 1, 4, 9, 0, 7, 12, 5, 7, 3};
System.out.println(Arrays.toString(arr));
selectionSort(arr);
System.out.println(Arrays.toString(arr));
}
}
冒泡排序:
package complexity01;
import java.util.Arrays;
/**
* @author Corley
* @date 2021/10/3 19:41
* @description LeetCodeAlgorithmZuo-complexity01
*/
public class BubbleSort {
public static void bubbleSort(int[] arr) {
if (null == arr || arr.length < 2) {
return;
}
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
}
private static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
public static void main(String[] args) {
int[] arr = new int[]{3, 2, 5, 1, 4, 9, 0, 7, 12, 5, 7, 3};
System.out.println(Arrays.toString(arr));
bubbleSort(arr);
System.out.println(Arrays.toString(arr));
}
}
这两种排序算法的效果不会受到数据的初始状态的影响。
插入排序:
package complexity01;
import java.util.Arrays;
/**
* @author Corley
* @date 2021/10/3 20:10
* @description LeetCodeAlgorithmZuo-complexity01
*/
public class InsertionSort {
public static void insertionSort(int[] arr) {
if (null == arr || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; i++) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
private static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
public static void main(String[] args) {
int[] arr = new int[]{3, 2, 5, 1, 4, 9, 0, 7, 12, 5, 7, 3};
System.out.println(Arrays.toString(arr));
insertionSort(arr);
System.out.println(Arrays.toString(arr));
}
}
插入排序的效果会受到数据的初始状态的影响,例如数组已经是有序的情况下。
额外空间复杂度:
你要实现一个算法流程,在实现算法流程的过程中,你需要开辟一些空间来支持你的算法流程。
作为输入参数的空间,不算额外空间;
作为输出结果的空间,也不算额外空间。
因为这些都是必要的、和现实目标有关的,所以都不算。
但除此之外,你的流程如果还需要开辟空间才能让你的流程继续下去。这部分空间就是额外空间。如果你的流程只需要开辟有限几个变量,额外空间复杂度就是O(1)。
算法流程的常数项的比拼方式:
放弃理论分析,生成随机数据直接测。为什么不去理论分析?
不是不能纯分析.而是没必要。因为不同常数时间的操作,虽然都是固定时间,但还是有快慢之分的。
比如,位运算的常数时间原小于算术运算的常数时间,这两个运算的常数时间又远小于数组寻址的时间。
所以如果纯理论分析,往往会需要非常多的分析过程。都已经到了具体细节的程度.莫不如交给实验数据好了。
常见的时间复杂度(我们陆续都会见到的):
排名从好到差:
O(1)
O(logN)
O(N)
O(N*logN)
O(N^2) O(N^3) … O(N^K)
O(2^N) O(3^N)… O(K^N)
O(N!)
算法和数据结构学习的大脉络:
1)知道怎么算的算法
2)知道怎么试的算法
3.对数器
对数器:
1,你想要测的方法a
2,实现复杂度不好但是容易实现的方法b,实现一个随机样本产生器
4,把方法a和方法b跑相同的随机样本,跑多次,看看得到的结果是否一样
5,如果有一个随机样本使得比对结果不一致,打印样本进行人工干预,改对方法a和方法b
6,当样本数量很多时比对测试依然正确,可以确定方法a已经正确。
4.二分法
二分法:
只要构建出能够排除另外一端的逻辑,就可以使用二分,而不一定需要保证数组有序。
应用:
1)在一个有序数组中,找某个数是否存在
package complexity01;
/**
* @author Corley
* @date 2021/10/4 9:03
* @description LeetCodeAlgorithmZuo-complexity01
*/
public class BinarySearchExist {
public static boolean exist(int[] arr, int num) {
if (null == arr || 0 == arr.length) {
return false;
}
int L = 0, R = arr.length - 1;
int mid;
while (L < R) {
mid = L + ((R - L) >> 1);
if (arr[mid] == num) {
return true;
} else if (arr[mid] < num) {
L = mid + 1;
} else {
R = mid - 1;
}
}
return arr[L] == num;
}
public static void main(String[] args) {
int[] arr = {0, 2, 5, 5, 6, 7, 7, 7, 9, 12};
System.out.println(exist(arr, 5));
System.out.println(exist(arr, 8));
System.out.println(exist(arr, 9));
}
}
2)在一个有序数组中,找>=某个数最左侧的位置
package complexity01;
/**
* @author Corley
* @date 2021/10/4 9:20
* @description LeetCodeAlgorithmZuo-complexity01
*/
public class BinarySearchNearLeft {
public static int nearestIndex(int[] arr, int num) {
int index = -1;
if (null == arr || 0 == arr.length) {
return index;
}
int L = 0, R = arr.length - 1;
int mid;
while (L <= R) {
mid = L + ((R - L) >> 1);
if (arr[mid] >= num) {
index = mid;
R = mid - 1;
} else {
L = mid + 1;
}
}
return index;
}
public static void main(String[] args) {
int[] arr = {0, 2, 5, 5, 6, 7, 7, 7, 9, 12};
System.out.println(nearestIndex(arr, 5));
System.out.println(nearestIndex(arr, 8));
System.out.println(nearestIndex(arr, 9));
}
}
3)在一个有序数组中,找<=某个数最右侧的位置
package complexity01;
/**
* @author Corley
* @date 2021/10/4 9:30
* @description LeetCodeAlgorithmZuo-complexity01
*/
public class BinarySearchNearRight {
public static int nearestIndex(int[] arr, int num) {
int index = -1;
if (null == arr || 0 == arr.length) {
return index;
}
int L = 0, R = arr.length - 1;
int mid;
while (L <= R) {
mid = L + ((R - L) >> 1);
if (arr[mid] <= num) {
index = mid;
L = mid + 1;
} else {
R = mid - 1;
}
}
return index;
}
public static void main(String[] args) {
int[] arr = {0, 2, 5, 5, 6, 7, 7, 7, 9, 12};
System.out.println(nearestIndex(arr, 5));
System.out.println(nearestIndex(arr, 8));
System.out.println(nearestIndex(arr, 9));
}
}
4)局部最小值问题
一个无序数组,任意两个相邻元素都不相等,找到一个局部最小值。
package complexity01;
/**
* @author Corley
* @date 2021/10/4 9:45
* @description LeetCodeAlgorithmZuo-complexity01
*/
public class BinarySearchLocalMin {
public static int getLessIndex(int[] arr) {
if (null == arr || 0 == arr.length) {
return -1;
}
if (1 == arr.length || arr[0] < arr[1]) {
return 0;
}
if (arr[arr.length - 1] < arr[arr.length - 2]) {
return arr.length - 1;
}
int left = 1, right = arr.length - 2;
int mid;
while (left < right) {
mid = left + ((right - left) >> 1);
if (arr[mid - 1] < arr[mid]) {
right = mid - 1;
} else if (arr[mid + 1] < arr[mid]) {
left = mid + 1;
} else {
return mid;
}
}
return left;
}
public static void main(String[] args) {
System.out.println(getLessIndex(new int[]{0, 2, 5, 5, 6, 7, 7, 7, 9, 12}));
System.out.println(getLessIndex(new int[]{8, 2, 5, 7, 6, 4, 7, 2, 3, 4}));
System.out.println(getLessIndex(new int[]{7, 2, 8, 5, 6, 9, 7, 3, 9, 0}));
}
}
5.异或运算
认识异或运算
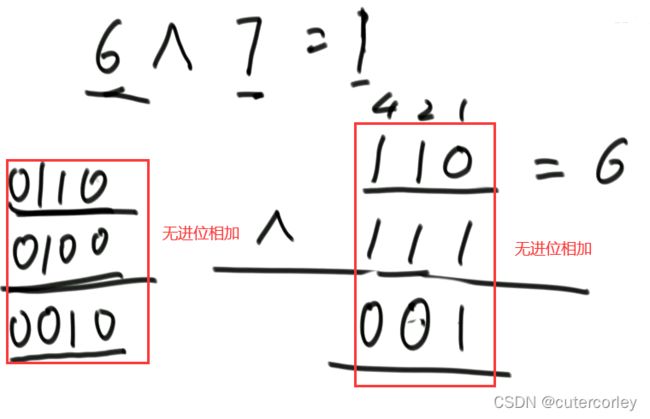
异或运算:相同为0,不同为1
同或运算:相同以1,不同为0
能长时间记住的概率接近0%
所以,异或运算就记成无进位相加!
异或运算的性质
1)0^N==N
N^N == 0
2)异或运算满足交换律和结合率
上面的两个性质用无进位相加来理解就非常的容易
如何不用额外变量交换两个数
可以进行这种操作的前提是变量属于不同的对象,即指向不同的内存,否则对象的数值会被置为0,但是允许两个对象的值相等。
一个数组中有一个数出现了奇数次,其他数都出现了偶数次,怎么找到并打印这一个数。
代码:
public static void getOneOddTimes(int[] arr) {
int eor = 0;
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
}
System.out.println(eor);
}
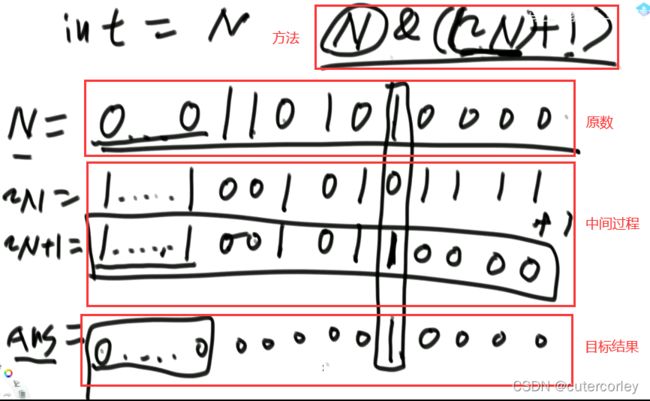
怎么把一个int类型的数,提取出最右侧的1
方法:N & ((~N) + 1)
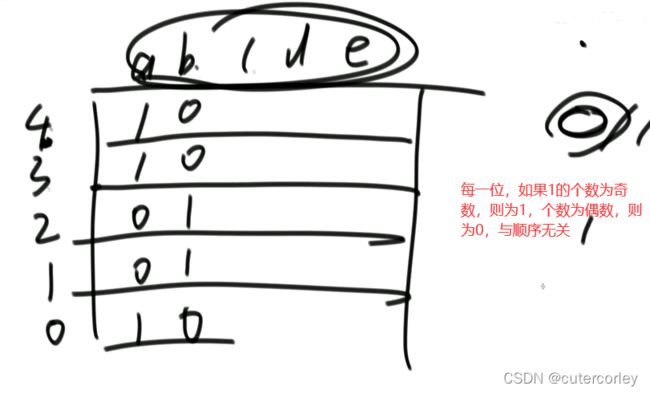
一个数组中有两个数出现了奇数次,其他数都出现了偶数次,怎么找到并打印这两个数。
如下:
/*
一个数组中有两个数出现了奇数次,其他数都出现了偶数次,怎么找到并打印这两个数。
*/
public static void getTwoOddTimes(int[] arr) {
int eor1 = 0;
for (int j : arr) {
eor1 ^= j;
}
// 提取最右边的1
int rightOne = eor1 & (~eor1 + 1);
int eor2 = 0;
for (int j : arr) {
if ((j & rightOne) != 0) {
eor2 ^= j;
}
}
int num1 = eor2, num2 = eor1 ^ eor2;
System.out.println(num1 + " " + num2);
}
public static void main(String[] args) {
int[] arr = {1, 2, 2, 4, 6, 6, 6, 6, 6, 4, 4, 4, 7, 7, 6, 7, 8, 8};
getTwoOddTimes(arr);
}
给定一个数,计算这个数的二进制形式中1的个数。
public static int bit1Count(int num) {
int count = 0;
int rightOne;
while (num != 0) {
rightOne = num & (~num + 1);
count++;
num ^= rightOne;
}
return count;
}
public static void main(String[] args) {
// int[] arr = {1, 2, 2, 4, 6, 6, 6, 6, 6, 4, 4, 4, 7, 7, 6, 7, 8, 8};
// getTwoOddTimes(arr);
System.out.println(Integer.toBinaryString(12345));
System.out.println(bit1Count(12345));
}
总结
左神极力推荐的对数器是检验算法实现正确性的有力工具,可以覆盖几乎所有情况的测试用例,无死角实现对算法的验证。同时异或也是可以在算法实现中加快运算效率的技巧。