RL 实践(1)—— 多臂赌博机
- 参考:《动手学强化学习》
- 多臂赌博机是一种简化版的强化学习问题,这种设定下只有动作和奖励,不存在状态信息(或者说全局只有一个状态,不存在状态转移)。在 RL 研究早期,很多关于评估性反馈的研究都是在这种 “非关联性的简化情况” 下进行的

- 关于多臂老虎机及相关算法原理的详细说明,请参考 强化学习笔记(2)—— 多臂赌博机,本文主要对平衡探索和利用的诸多方法进行编程实践
- 注意:由于本文是jupyter文档转换来的,代码不一定可以直接运行,有些注释是jupyter给出的交互结果,而非运行结果!!
文章目录
- 1. 多臂老虎机
-
- 1.1 问题设定
- 1.2 形式化描述
- 1.3 程序实现
- 2. 各种平衡探索和利用的策略
-
- 2.1 ϵ \epsilon ϵ - greedy
- 2.2 Decaying ϵ \epsilon ϵ - greedy
- 2.3 基于置信度上界的动作选择(UCB)
- 2.4 汤普森采样算法(Thompson sampling)
- 3. 总结
1. 多臂老虎机
1.1 问题设定
-
多臂老虎机(multi-armed bandit,MAB)有k个摇臂,每拉动一个摇臂,都会落下一些金币。每个拉杆都对应一个关于即时金币收益的未知分布,应该使用什么策略,才能在有限的尝试次数中获得最多金币呢?

如果拉杆的收益分布已知,直接使用贪心策略一直拉最优拉杆即可,但当分布未知时,我们一方面需要足够多的交互来估计拉杆的期望收益,另一方面又要充分利用当前的估计结果尽量最大化收益,这个简单的问题很好地反映了强化学习中的 “探索-利用困境”
-
多臂老虎机问题相比完整 RL 问题的显著简化是不存在状态转移。不妨设系统一直处于一个固定状态 s s s,操作第 i i i 根拉杆记为动作 a i a_i ai,则该设定下任何 ( s , a i ) (s,a_i) (s,ai) 的真实价值 Q ( s , a i ) Q(s,a_i) Q(s,ai) 都仅和此处的即时 reward r ( s , a i ) r(s,a_i) r(s,ai) 相关,所有反馈都是纠正性反馈,可以保证(交互次数足够多时)经验期望就是对真实价值的良好估计。因此我们不用特别考虑价值估计方法导致的误差,特别适合研究如何平衡开发和试探
1.2 形式化描述
- 多臂老虎机问题可以表示为一个元组 < A , R > <\mathcal{A,R}> <A,R>,其中 A \mathcal{A} A 是动作集合, R \mathcal{R} R 是 reward 概率分布,拉动每一根拉杆的动作 a a a 都对应一个奖励概率分布 R ( r ∣ a ) \mathcal{R}(r|a) R(r∣a),不同拉杆的奖励分布通常是不同的
- MAB 的优化目标:最大化有限时间 T T T 内的累积奖励
G T = max ∑ t = 1 T r t , r t ∼ R ( ⋅ ∣ a t ) G_T = \max\sum_{t=1}^T r_t ,\quad r_t \sim \mathcal{R}(·|a_t) GT=maxt=1∑Trt,rt∼R(⋅∣at)
对于每个动作定义其价值为期望 reward,即 Q ( a ) = E r ∼ R ( ⋅ ∣ a ) [ r ] Q(a)=\mathbb{E}_{r\sim\mathcal{R}(·|a)}[r] Q(a)=Er∼R(⋅∣a)[r],最优动作具有最大的价值 Q ∗ = max a ∈ A Q ( a ) Q^*=\max_{a\in\mathcal{A}}Q(a) Q∗=maxa∈AQ(a)。定义后悔为拉动当前拉杆的动作 a a a 与最优拉杆的期望奖励差(价值差) R ( a ) = Q ∗ − Q ( a ) R(a)=Q^*-Q(a) R(a)=Q∗−Q(a),则一次完整的 T T T 步决策的累计后悔为 σ R = ∑ t = 1 T R ( a t ) \sigma_R = \sum_{t=1}^T R(a_t) σR=∑t=1TR(at)。MAB 的优化目标最大化累积奖励等价于最小化累积懊悔 - 本文在 “计算经验期望作为价值估计” 和 “平均实验结果” 时都使用增量式的求均值方法,以价值估计为例,更新公式如下
Q n + 1 = 1 n ∑ i = 1 n R i = 1 n ( R n + ∑ i = 1 n − 1 R i ) = 1 n ( R n + ( n − 1 ) 1 ( n − 1 ) ∑ i = 1 n − 1 R i ) = 1 n ( R n + ( n − 1 ) Q n ) = 1 n ( R n + n Q n − Q n ) = Q n + 1 n [ R n − Q n ] \begin{aligned} Q_{n+1} &= \frac{1}{n} \sum_{i=1}^n R_i \\ &= \frac{1}{n}(R_n+\sum_{i=1}^{n-1}R_i) \\ &= \frac{1}{n}(R_n+(n-1)\frac{1}{(n-1)}\sum_{i=1}^{n-1}R_i) \\ &= \frac{1}{n}(R_n+(n-1)Q_n) \\ &= \frac{1}{n}(R_n + nQ_n-Q_n) \\ &= Q_n + \frac{1}{n}[R_n-Q_n] \end{aligned} Qn+1=n1i=1∑nRi=n1(Rn+i=1∑n−1Ri)=n1(Rn+(n−1)(n−1)1i=1∑n−1Ri)=n1(Rn+(n−1)Qn)=n1(Rn+nQn−Qn)=Qn+n1[Rn−Qn]
1.3 程序实现
- 这里实现高斯分布和伯努利分布的两个赌博机类,后面实验会用到
from typing import Tuple from scipy import stats import numpy as np import matplotlib.pyplot as plt from abc import ABCMeta import abc import seaborn as sns import matplotlib.pyplot as plt import pandas as pd class BernoulliBandit: """ K臂伯努利多臂老虎机, 每个拉杆有p的概率 reward=1, 1-p 概率 reward=0, p 从0-1均匀分布采样 """ def __init__(self, K): self.K = K self.values = np.random.uniform(size=K) # 随机生成K个0~1的数, 作为拉动每根拉杆的期望reward self.bestAction = np.argmax(self.values) # 获奖概率最大的拉杆 def step(self, k): return np.random.rand() < self.values[k] # python 中 True/False 等价于 1/0 class GaussBandit: """ K臂高斯老虎机, 每个拉杆期望收益采样自标准正态分布, 即时 reward 是收益期望加上高斯噪声 """ def __init__(self, K=10): self.K = K # 摇臂数量 self.values = np.random.randn(K) # 从标准正态分布采样K个拉杆的收益均值 self.bestAction = np.argmax(self.values) # 最优动作索引 def step(self, k): return np.random.normal(loc=self.values[k], scale=1, size=1) def showDistribution(self): # 绘制K个拉杆即时 reward 分布的小提琴图 fig = plt.figure(figsize=(8,5)) foo = pd.DataFrame(columns =['Arm','Reward']) for i in range(10): foo.loc[i] = ['no'+str(i+1),np.random.normal(loc=self.values[i], scale=1, size=1000)] foo = foo.explode('Reward') foo['Reward'] = foo['Reward'].astype('float') sns.violinplot(data=foo, x='Arm', y='Reward') plt.show() # 随机生成一个10臂高斯老虎机,观察拉杆 reward 分布 bandit = GaussBandit(10) bandit.showDistribution()
2. 各种平衡探索和利用的策略
-
在多臂老虎机乃至完整 RL 问题中,平衡探索和利用的常用思路是在开始时做比较多的探索,在对每根拉杆都有比较准确的估计后,再进行利用。目前已有一些比较经典的算法来解决这个问题,例如 ϵ \epsilon ϵ-贪婪算法、上置信界算法和汤普森采样算法等,我们接下来将分别介绍这几种算法
-
首先定义求解器的基类
class Solver(metaclass=ABCMeta): """ 多臂老虎机算法基本框架 """ def __init__(self, bandit, initValues): self.bandit = bandit self.counts = np.zeros(self.bandit.K) # 每根拉杆的尝试次数 self.initValues = initValues self.qValues = initValues # 当前价值估计 @abc.abstractmethod def run_one_step(self) -> Tuple[int, float]: # 返回当前动作选择的拉杆索引以及即时reward, 由每个具体的策略实现 pass def rollout(self,num_steps): # 运行 num_steps 次 G, B, R = 0,0,0 # 当前收益, 当前最优选择次数, 当前步的累积懊悔 returnCurve = np.zeros(num_steps) # 收益曲线 proportionCurve = np.zeros(num_steps) # 比例曲线 regretCurve = np.zeros(num_steps) # 后悔曲线 self.counts = np.zeros(self.bandit.K) # 计数清零 self.qValues = self.initValues # 初始化价值估计 for i in range(num_steps): k, r = self.run_one_step() self.counts[k] += 1 self.qValues[k] += 1. / (self.counts[k]) * (r - self.qValues[k]) B += (k == self.bandit.bestAction) G += r R += self.bandit.values[self.bandit.bestAction] - self.bandit.values[k] returnCurve[i] = G/(i+1) proportionCurve[i] = B/(i+1) regretCurve[i] = R return returnCurve, proportionCurve, regretCurve -
定义测试和绘图的代码
def plot(banditParas, sloverParas): """ 绘制收益、最优动作比例以及累计后悔曲线 """ banditClass, banditArms, banditNum, banditSteps = banditParas sloverClass, initValues, sloverSettings = sloverParas # 解决 plt 中文显示的问题 plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False fig = plt.figure(figsize=(9,9)) a1 = fig.add_subplot(3,1,1,label='a1') a2 = fig.add_subplot(3,1,2,label='a2') a3 = fig.add_subplot(3,1,3,label='a3') a1.set_xlabel('训练步数') a1.set_ylabel('平均收益') a2.set_xlabel('训练步数') a2.set_ylabel('最优动作比例') a3.set_xlabel('训练步数') a3.set_ylabel('后悔') # 测试各种设置 for setting in sloverSettings: paraLabel = setting[0] # 实例化 Num 个赌博机 aveRCurve, avePCurve, aveRegCurve = np.zeros(banditSteps), np.zeros(banditSteps), np.zeros(banditSteps) for i in range(banditNum): bandit = banditClass(banditArms) solver = sloverClass(*(bandit,initValues)+setting[1:]) returnCurve, proportionCurve, regretCurve = solver.rollout(banditSteps) aveRCurve += 1/(i+1)*(returnCurve-aveRCurve) # 增量式计算均值 avePCurve += 1/(i+1)*(proportionCurve-avePCurve) # 增量式计算均值 aveRegCurve += 1/(i+1)*(regretCurve-aveRegCurve) # 增量式计算均值 a1.plot(aveRCurve,'-',linewidth=2, label=paraLabel) a2.plot(avePCurve,'-',linewidth=2, label=paraLabel) a3.plot(aveRegCurve,'-',linewidth=2, label=paraLabel) a1.legend(fontsize=10) # 显示图例,即每条线对应 label 中的内容 a2.legend(fontsize=10) a3.legend(fontsize=10) plt.show() def plotRegret(banditParas, sloverParas): """ 只绘制后悔曲线 """ banditClass, banditArms, banditNum, banditSteps = banditParas sloverClass, initValues, sloverSettings = sloverParas # 解决 plt 中文显示的问题 plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False fig = plt.figure(figsize=(10,5)) a1 = fig.add_subplot(1,1,1,label='a1') a1.set_xlabel('训练步数') a1.set_ylabel('后悔') # 测试各种设置 for setting in sloverSettings: paraLabel = setting[0] # 实例化 Num 个赌博机 aveRegCurve = np.zeros(banditSteps) for i in range(banditNum): bandit = banditClass(banditArms) solver = sloverClass(*(bandit,initValues)+setting[1:]) _, _, regretCurve = solver.rollout(banditSteps) aveRegCurve += 1.0/(i+1)*(regretCurve-aveRegCurve) # 增量式计算均值 a1.plot(aveRegCurve,'-',linewidth=2, label=paraLabel) a1.legend(fontsize=10) # 显示图例,即每条线对应 label 中的内容 plt.show()
2.1 ϵ \epsilon ϵ - greedy
-
如下选择动作,以较大概率进行贪心利用,同时以 ϵ \epsilon ϵ 小概率随机探索
a t ← { arg max a Q ( a ) with probability 1 − ε a random action with probability ε a_t \leftarrow \begin{cases}\arg \max _a Q(a) & \text { with probability } 1-\varepsilon \\ \text { a random action } & \text { with probability } \varepsilon\end{cases} at←{argmaxaQ(a) a random action with probability 1−ε with probability ε使用10臂高斯赌博机进行测试
class EpsilonGreedy(Solver): """ epsilon贪婪算法,继承Solver类 """ def __init__(self, *args): bandit, initValues, epsilon = args super(EpsilonGreedy, self).__init__(bandit, initValues) self.epsilon = epsilon def run_one_step(self): if np.random.binomial(1,self.epsilon) == 1: k = np.random.randint(self.bandit.K) # 随机选择一根拉杆 else: k = np.random.choice([a for a in range(self.bandit.K) if self.qValues[a] == np.max(self.qValues)]) r = self.bandit.step(k) # 得到本次动作的奖励 return k, r if __name__ == '__main__': K = 10 # 摇臂数 NUM = 100 # 赌博机数量 STEPS = 4000 # 交互次数 banditParas = (GaussBandit, K, NUM, STEPS) sloverSettings = [('0.001-greedy', 0.001), ('0.1-greedy',0.1), ('0.15-greedy',0.15), ('0.25-greedy',0.25), ('0.50-greedy',0.50)] sloverParas = (EpsilonGreedy, np.ones(K), sloverSettings) # 根据参数列表进行对比试验 plot(banditParas, sloverParas)
- 观察实验结果发现
- 随机探索比例 ϵ \epsilon ϵ 太大会导致性能上限下降,最终次优收敛
- 随机探索比例 ϵ \epsilon ϵ 太小会导致收敛缓慢
- 无论 ϵ \epsilon ϵ 如何取值,累计后悔最终都是线性增长的,这是因早期确定最优动作后就会较高比例一直执行它,其他动作只有 ϵ \epsilon ϵ 概率访问,即使真的是更优动作也需要较长时间收敛实现替代。如果贪心动作一直没有变化,则策略是固定的,每一步交互的期望后悔都一致。另外注意到上图中 0.001-greedy 曲线斜率在后期变平缓,说明它在后期已经实现了最优动作的替代,如果所有策略都找到了真正的最优动作,则累计后悔曲线的斜率和 ϵ \epsilon ϵ 成正比例
- 注意到 ϵ \epsilon ϵ - greedy 方法一直以固定的比例进行探索和利用,因而很容易落入一个静态策略,导致累计后悔线性增长,我们希望随着交互的增加,对系统理解的越来越深入,策略应能一直动态调整探索和利用的倾向性。下面介绍的几个方法都针对该问题进行了改进,为了简便考虑,下面方法统一使用伯努利赌博机,只观察后悔曲线
2.2 Decaying ϵ \epsilon ϵ - greedy
- 注意到 ϵ \epsilon ϵ 控制着探索的比例,因此简单地使 ϵ \epsilon ϵ 随时间减小就能达到 “早期重探索,晚期重利用” 的效果。下面设置 ϵ = 100 t \epsilon=\frac{100}{t} ϵ=t100 进行实验
注:这里理论上应该设 ϵ = 1 t \epsilon=\frac{1}{t} ϵ=t1,以保证 ϵ < 1 \epsilon<1 ϵ<1 是一个合法的概率,但是测试发现这样的探索还是有点不足,这里简单地增大分子就能在早期进行更多的纯随机试探
- 使用伯努利赌博机测试,观察后悔曲线
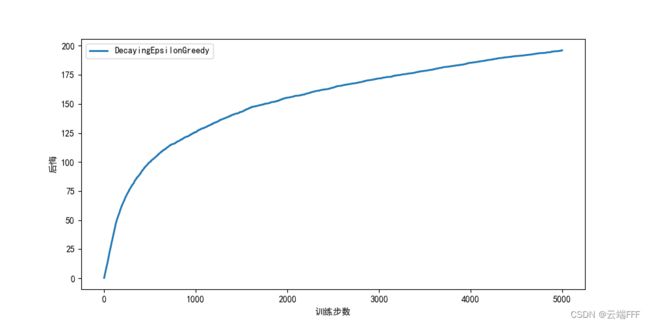
class DecayingEpsilonGreedy(Solver): """ epsilon值随时间衰减的epsilon-贪婪算法,继承Solver类 """ def __init__(self, *args): bandit, initValues = args super(DecayingEpsilonGreedy, self).__init__(bandit, initValues) self.total_count = 0 def run_one_step(self): self.total_count += 1 if np.random.random() < 100 / self.total_count: # 试探概率(epsilon)值随时间衰减,这里分子可以设置超过 1 来增强随机探索 k = np.random.randint(0, self.bandit.K) else: k = np.random.choice([a for a in range(self.bandit.K) if self.qValues[a] == np.max(self.qValues)]) r = self.bandit.step(k) return k, r if __name__ == '__main__': K = 10 # 摇臂数 NUM = 10 # 赌博机数量 STEPS = 5000 # 交互次数 #np.random.seed(0) banditParas = (BernoulliBandit, K, NUM, STEPS) sloverParas = (DecayingEpsilonGreedy, np.ones(K), [('DecayingEpsilonGreedy',)]) plotRegret(banditParas, sloverParas)
- 从实验结果图中可以发现,随时间做反比例衰减的 ϵ \epsilon ϵ - greedy 算法能够使累积懊悔与时间步的关系变成次线性(sublinear)的,这明显优于固定 ϵ \epsilon ϵ 值的 ϵ \epsilon ϵ-greedy 算法
- Decaying ϵ \epsilon ϵ - greedy 方法的问题在于 ϵ \epsilon ϵ 的衰减过程是启发式设定的,并不能根据实际价值估计情况实现探索利用的自动权衡,只是强行实现了 “早期重探索,晚期重利用” 的效果
2.3 基于置信度上界的动作选择(UCB)
- 综合考虑 “动作价值估计有多接近最大值” 以及 “估计的不确定性” 这两个因素,根据下式选择动作
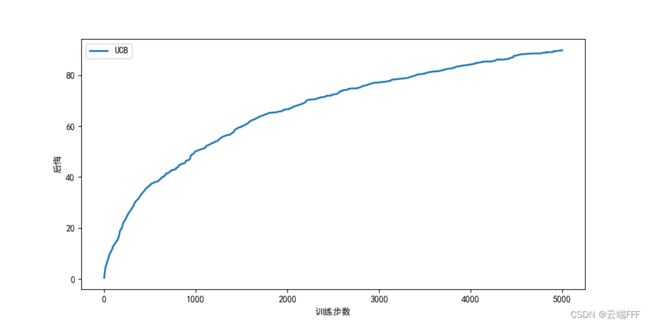
a t = arg max a [ Q ^ t ( a ) + c l n t 2 ( N t ( a ) + 1 ) ] a_t =\argmax_a\big[\hat{Q}_t(a)+c\sqrt{\frac{lnt}{2(N_t(a)+1)}}\big] at=aargmax[Q^t(a)+c2(Nt(a)+1)lnt] 其中开方项代表对估计不确定性的度量, c c c 为考虑不确定性的程度超参数, N t ( a ) N_t(a) Nt(a) 代表时刻 t t t 之前 a 被选择的次数,对它加 1 以免分母出现 0。这个式子来自于霍夫丁不等式,具体推导和说明请参考 强化学习笔记(2)—— 多臂赌博机 第 5 节 - 使用伯努利赌博机测试,观察后悔曲线
class UCB(Solver): """ UCB算法,继承Solver类 """ def __init__(self, *args): bandit, initValues, coef = args super(UCB, self).__init__(bandit, initValues) self.total_count = 0 self.coef = coef def run_one_step(self): self.total_count += 1 ucb = self.qValues + self.coef * np.sqrt(np.log(self.total_count) / (2 * (self.counts + 1))) # 计算上置信界 k = np.argmax(ucb) # 选出上置信界最大的拉杆 r = self.bandit.step(k) return k, r if __name__ == '__main__': K = 10 # 摇臂数 NUM = 10 # 赌博机数量 STEPS = 5000 # 交互次数 #np.random.seed(0) banditParas = (BernoulliBandit, K, NUM, STEPS) sloverParas = (UCB, np.ones(K), [('UCB',1)]) plotRegret(banditParas, sloverParas)
2.4 汤普森采样算法(Thompson sampling)
-
汤普森采样(Thompson sampling)是适用于 MAB 问题的一个经典算法,其核心思想就是利用交互数据直接估计出各个拉杆的奖励分布 R ( r ∣ a ) \mathcal{R}(r|a) R(r∣a),然后根据它来选择动作。具体实现时- 使用 Beta 分布对拉杆 reward 分布进行建模(因此只适用于伯努利赌博机),关于 beta 分布请参考这里
- 由于计算所有拉杆分布 R ( r ∣ a ) \mathcal{R}(r|a) R(r∣a) 期望的代价比较高,汤普森采样算法使用采样的方式,每轮迭代根据当前每个动作的估计分布 R ( r ∣ a ) \mathcal{R}(r|a) R(r∣a) 进行一轮采样,选择样本中奖励最大的动作执行,示例如下
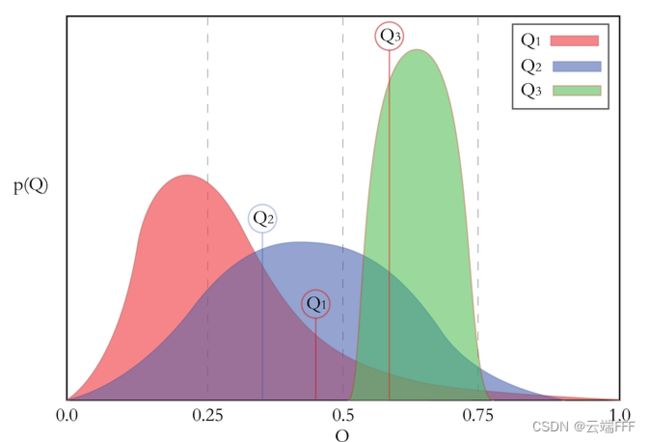
这里三个颜色就是三个动作的估计 R ( r ∣ a ) \mathcal{R}(r|a) R(r∣a) 分布, Q 1 , Q 2 , Q 3 Q_1,Q_2,Q_3 Q1,Q2,Q3 则是一轮采样得到的结果, Q 3 Q_3 Q3 最大,执行动作 a 3 a_3 a3
-
使用伯努利赌博机测试,观察后悔曲线
class ThompsonSampling(Solver): """ 汤普森采样算法,继承Solver类 """ def __init__(self, *args): bandit, initValues = args super(ThompsonSampling, self).__init__(bandit, initValues) # 这里 initValues 其实没用 self._a = np.ones(self.bandit.K) # 列表,表示每根拉杆奖励为1的次数 self._b = np.ones(self.bandit.K) # 列表,表示每根拉杆奖励为0的次数 def run_one_step(self): samples = np.random.beta(self._a, self._b) # 按照Beta分布采样一组奖励样本 k = np.argmax(samples) # 选出采样奖励最大的拉杆 r = self.bandit.step(k) self._a[k] += r # 更新Beta分布的第一个参数 self._b[k] += (1 - r) # 更新Beta分布的第二个参数 return k, r if __name__ == '__main__': K = 10 # 摇臂数 NUM = 10 # 赌博机数量 STEPS = 5000 # 交互次数 #np.random.seed(0) banditParas = (BernoulliBandit, K, NUM, STEPS) sloverParas = (ThompsonSampling, np.ones(K), [('ThompsonSampling',)]) plotRegret(banditParas, sloverParas)
3. 总结
- 本文在多臂赌博机环境下编程验证了四种常用的平衡探索和利用的方法
- ϵ \epsilon ϵ - greedy:思想最简单,始终以固定的比例进行探索和利用,容易落入一个静态策略,累计后悔线性增长
- Decaying ϵ \epsilon ϵ - greedy:使 ϵ \epsilon ϵ - greedy 中的 ϵ \epsilon ϵ 逐渐减小,实现 “早期重探索,晚期重利用” 的效果,可以使累积懊悔随时间次线性增长,但是 ϵ \epsilon ϵ 减小曲线是手工设定,不能完全匹配实际情况
- 上置信界算法:综合考虑 “动作价值估计有多接近最大值” 以及 “估计的不确定性” 这两个因素设计的指标,可以使累积懊悔随时间次线性增长,能一定程度匹配实际情况,不易推广到完整 RL 问题
- 汤普森采样算法:利用交互数据建模真实分布,再用蒙特卡洛采样选择动作的方法,最能匹配实际情况,但是仅适用于伯努利赌博机,而且没有价值估计的概念了,无法推广到完整 RL 问题
- 最后给出完整代码,可以直接复制粘贴到 vscode 运行
from typing import Tuple from scipy import stats import numpy as np import matplotlib.pyplot as plt from abc import ABCMeta import abc import seaborn as sns import matplotlib.pyplot as plt import pandas as pd # ======================================= 老虎机 ================================================= class BernoulliBandit: """ K臂伯努利多臂老虎机, 每个拉杆有p的概率 reward=1, 1-p 概率 reward=0, p 从0-1均匀分布采样 """ def __init__(self, K): self.K = K self.values = np.random.uniform(size=K) # 随机生成K个0~1的数, 作为拉动每根拉杆的期望reward self.bestAction = np.argmax(self.values) # 获奖概率最大的拉杆 def step(self, k): return np.random.rand() < self.values[k] # python 中 True/False 等价于 1/0 class GaussBandit: """ K臂高斯老虎机, 每个拉杆期望收益采样自标准正态分布, 即时 reward 是收益期望加上高斯噪声 """ def __init__(self, K=10): self.K = K # 摇臂数量 self.values = np.random.randn(K) # 从标准正态分布采样K个拉杆的收益均值 self.bestAction = np.argmax(self.values) # 最优动作索引 def step(self, k): return np.random.normal(loc=self.values[k], scale=1, size=1) def showDistribution(self): # 绘制K个拉杆即时 reward 分布的小提琴图 fig = plt.figure(figsize=(8,5)) foo = pd.DataFrame(columns =['Arm','Reward']) for i in range(10): foo.loc[i] = ['no'+str(i+1),np.random.normal(loc=self.values[i], scale=1, size=1000)] foo = foo.explode('Reward') foo['Reward'] = foo['Reward'].astype('float') sns.violinplot(data=foo, x='Arm', y='Reward') #plt.show() # ======================================= 选择动作的策略 ================================================= class Solver(metaclass=ABCMeta): """ 多臂老虎机算法基本框架 """ def __init__(self, bandit, initValues): self.bandit = bandit self.counts = np.zeros(self.bandit.K) # 每根拉杆的尝试次数 self.initValues = initValues self.qValues = initValues # 当前价值估计 @abc.abstractmethod def run_one_step(self) -> Tuple[int, float]: # 返回当前动作选择的拉杆索引以及即时reward, 由每个具体的策略实现 pass def rollout(self,num_steps): # 运行 num_steps 次 G, B, R = 0,0,0 # 当前收益, 当前最优选择次数, 当前步的累积懊悔 returnCurve = np.zeros(num_steps) # 收益曲线 proportionCurve = np.zeros(num_steps) # 比例曲线 regretCurve = np.zeros(num_steps) # 后悔曲线 self.counts = np.zeros(self.bandit.K) # 计数清零 self.qValues = self.initValues # 初始化价值估计 for i in range(num_steps): k, r = self.run_one_step() self.counts[k] += 1 self.qValues[k] += 1. / (self.counts[k]) * (r - self.qValues[k]) B += (k == self.bandit.bestAction) G += r R += self.bandit.values[self.bandit.bestAction] - self.bandit.values[k] returnCurve[i] = G/(i+1) proportionCurve[i] = B/(i+1) regretCurve[i] = R return returnCurve, proportionCurve, regretCurve class EpsilonGreedy(Solver): """ epsilon贪婪算法,继承Solver类 """ def __init__(self, *args): bandit, initValues, epsilon = args super(EpsilonGreedy, self).__init__(bandit, initValues) self.epsilon = epsilon def run_one_step(self): if np.random.binomial(1,self.epsilon) == 1: k = np.random.randint(self.bandit.K) else: k = np.random.choice([a for a in range(self.bandit.K) if self.qValues[a] == np.max(self.qValues)]) r = self.bandit.step(k) return k, r class DecayingEpsilonGreedy(Solver): """ epsilon值随时间衰减的epsilon-贪婪算法,继承Solver类 """ def __init__(self, *args): bandit, initValues = args super(DecayingEpsilonGreedy, self).__init__(bandit, initValues) self.total_count = 0 def run_one_step(self): self.total_count += 1 if np.random.random() < 100 / self.total_count: # 试探概率(epsilon)值随时间衰减,这里分子可以设置超过 1 来增强随机探索 k = np.random.randint(0, self.bandit.K) else: k = np.random.choice([a for a in range(self.bandit.K) if self.qValues[a] == np.max(self.qValues)]) r = self.bandit.step(k) return k, r class UCB(Solver): """ UCB算法,继承Solver类 """ def __init__(self, *args): bandit, initValues, coef = args super(UCB, self).__init__(bandit, initValues) self.total_count = 0 self.coef = coef def run_one_step(self): self.total_count += 1 ucb = self.qValues + self.coef * np.sqrt(np.log(self.total_count) / (2 * (self.counts + 1))) # 计算上置信界 k = np.argmax(ucb) # 选出上置信界最大的拉杆 r = self.bandit.step(k) return k, r class ThompsonSampling(Solver): """ 汤普森采样算法,继承Solver类 """ def __init__(self, *args): bandit, initValues = args super(ThompsonSampling, self).__init__(bandit, initValues) # 这里 initValues 其实没用 self._a = np.ones(self.bandit.K) # 列表,表示每根拉杆奖励为1的次数 self._b = np.ones(self.bandit.K) # 列表,表示每根拉杆奖励为0的次数 def run_one_step(self): samples = np.random.beta(self._a, self._b) # 按照Beta分布采样一组奖励样本 k = np.argmax(samples) # 选出采样奖励最大的拉杆 r = self.bandit.step(k) self._a[k] += r # 更新Beta分布的第一个参数 self._b[k] += (1 - r) # 更新Beta分布的第二个参数 return k, r # ======================================= 绘图方法 ================================================= def plot(banditParas, sloverParas): """ 绘制收益、最优动作比例以及后悔曲线 """ banditClass, banditArms, banditNum, banditSteps = banditParas sloverClass, initValues, sloverSettings = sloverParas # 解决 plt 中文显示的问题 plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False fig = plt.figure(figsize=(9,9)) a1 = fig.add_subplot(3,1,1,label='a1') a2 = fig.add_subplot(3,1,2,label='a2') a3 = fig.add_subplot(3,1,3,label='a3') a1.set_xlabel('训练步数') a1.set_ylabel('平均收益') a2.set_xlabel('训练步数') a2.set_ylabel('最优动作比例') a3.set_xlabel('训练步数') a3.set_ylabel('后悔') # 测试各种设置 for setting in sloverSettings: paraLabel = setting[0] # 实例化 Num 个赌博机 aveRCurve, avePCurve, aveRegCurve = np.zeros(banditSteps), np.zeros(banditSteps), np.zeros(banditSteps) for i in range(banditNum): bandit = banditClass(banditArms) solver = sloverClass(*(bandit,initValues)+setting[1:]) returnCurve, proportionCurve, regretCurve = solver.rollout(banditSteps) aveRCurve += 1/(i+1)*(returnCurve-aveRCurve) # 增量式计算均值 avePCurve += 1/(i+1)*(proportionCurve-avePCurve) # 增量式计算均值 aveRegCurve += 1/(i+1)*(regretCurve-aveRegCurve) # 增量式计算均值 a1.plot(aveRCurve,'-',linewidth=2, label=paraLabel) a2.plot(avePCurve,'-',linewidth=2, label=paraLabel) a3.plot(aveRegCurve,'-',linewidth=2, label=paraLabel) a1.legend(fontsize=10) # 显示图例,即每条线对应 label 中的内容 a2.legend(fontsize=10) a3.legend(fontsize=10) plt.show() def plotRegret(banditParas, sloverParas): """ 只绘制后悔曲线 """ banditClass, banditArms, banditNum, banditSteps = banditParas sloverClass, initValues, sloverSettings = sloverParas # 解决 plt 中文显示的问题 plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False fig = plt.figure(figsize=(10,5)) a1 = fig.add_subplot(1,1,1,label='a1') a1.set_xlabel('训练步数') a1.set_ylabel('后悔') # 测试各种设置 for setting in sloverSettings: paraLabel = setting[0] # 实例化 Num 个赌博机 aveRegCurve = np.zeros(banditSteps) for i in range(banditNum): bandit = banditClass(banditArms) solver = sloverClass(*(bandit,initValues)+setting[1:]) _, _, regretCurve = solver.rollout(banditSteps) aveRegCurve += 1.0/(i+1)*(regretCurve-aveRegCurve) # 增量式计算均值 a1.plot(aveRegCurve,'-',linewidth=2, label=paraLabel) a1.legend(fontsize=10) # 显示图例,即每条线对应 label 中的内容 plt.show() if __name__ == '__main__': K = 10 # 摇臂数 NUM = 10 # 赌博机数量 STEPS = 4000 # 交互次数 # 高斯老虎机 + epsilon-greedy 完整测试 banditParas = (GaussBandit, K, NUM, STEPS) sloverSettings = [('0.001-greedy', 0.001), ('0.1-greedy',0.1), ('0.15-greedy',0.15), ('0.25-greedy',0.25), ('0.50-greedy',0.50)] sloverParas = (EpsilonGreedy, np.ones(K), sloverSettings) plot(banditParas, sloverParas) ''' # 伯努利老虎机 + epsilon-greedy 观察后悔曲线线性增长 banditParas = (BernoulliBandit, K, NUM, STEPS) sloverSettings = [('0.001-greedy', 0.001), ('0.1-greedy',0.1), ('0.15-greedy',0.15), ('0.25-greedy',0.25), ('0.50-greedy',0.50), ('0.75-greedy',0.75), ('1.00-greedy',1.00)] sloverParas = (EpsilonGreedy, np.ones(K), sloverSettings) plotRegret(banditParas, sloverParas) ''' ''' # 伯努利老虎机 + decaying epsilon-greedy 观察后悔曲线对数增长 banditParas = (BernoulliBandit, K, NUM, STEPS) sloverParas = (DecayingEpsilonGreedy, np.ones(K), [('DecayingEpsilonGreedy',)]) plotRegret(banditParas, sloverParas) ''' ''' # 伯努利老虎机 + UCB 观察后悔曲线对数增长 banditParas = (BernoulliBandit, K, NUM, STEPS) sloverParas = (UCB, np.ones(K), [('UCB',1)]) plotRegret(banditParas, sloverParas) ''' ''' # 伯努利老虎机 + ThompsonSampling 观察后悔曲线对数增长 banditParas = (BernoulliBandit, K, NUM, STEPS) sloverParas = (ThompsonSampling, np.ones(K), [('ThompsonSampling',)]) plotRegret(banditParas, sloverParas) '''