强化学习: 策略迭代与价值迭代

强化学习面试经典问题: 策略迭代与价值迭代的关系

在强化学习问题中, 如果知道环境的模型(动力学模型Model-based, 例如所有的状态转移概率矩阵$P(s^{\prime }|s)$等), 则可利用这些信息构建一个 MDP 模型来对环境进行描述. 一旦有了环境的动力学模型, 就可以使用动态规划(DP)的方法来对最优价值函数和策略进行求解. 一旦获得了最优价值函数$V_{\pi }^{\ast }(s)$, 最优策略就是选择能够最大化下一状态价值的动作.

总结:

相同点: 都用于求解 Model-Based 的DP算法.
异同点:

1. 价值迭代不直接改进策略; 策略迭代直接改进策略: 值函数和策略同时达到最优; 策略迭代先是① 策略评估, 后是② 策略提升
2. 价值迭代采用的是贝尔曼最优方程，策略迭代采用的是贝尔曼方程
3. 在状态空间较小时, 策略迭代的收敛速度更快一些. 在状态空间较大时, 不适合用策略迭代.

策略迭代:

策略迭代(Policy Iteration)就是在策略$\pi (a│s)$未知的情况下，根据每次迭代的反馈reward来学到最优$\pi (a│s)$.
策略迭代的主要时间都花费在策略评估上，对一个简单的问题来说，在策略评估上花费的时间不算长；但对复杂的问题来说，这个步骤的时间比较长. 但是其优点也很明显，就是很容易证明其收敛性.

其算法思想是:

1. 首先随机初始化策略$\pi (a│s)$, 将状态价值函数$V_{\pi }(s)$置为 0
2. 在①策略评估部分, 根据当前的策略$\pi (a│s)$来计算每一个状态的价值$V_{\pi }(s)$, 直到$V_{\pi }(s)$收敛为止: $V(s)\leftarrow {\sum }_{(}r,s^{\prime })(r+\gamma V(s^{\prime }))\cdot P(r,s^{\prime }|s,\pi (s))$
3. 在②策略改进部分, 根据上一步求得的状态价值$V_{\pi }(s)$来得到新的策略$\pi (a│s)$, 直到策略$\pi (a│s)$收敛为止, 否则重新回到策略估计: $\pi (s)\leftarrow argma{x}_a{\sum }_{r,s^{\prime }}(r+\gamma V(s^{\prime }))\cdot P(r,s^{\prime }|s,\pi (s))$

---

首先随机初始化随机策略$\pi$, 将所有状态$s$的价值函数置为$V_{\pi }(s)=0$

一直进行迭代步骤①+②, 直到$\pi (a│s)$收敛(两次迭代之间变化不大):
①策略评估: 根据当前的策略π来计算所有状态$s$的价值$V_{\pi }(s)$, 直到收敛为止. 执行$n$轮迭代, 每轮迭代时计算出每个状态$s$的$V_{\pi }(s)$, 直到$V_{\pi }(s)$变化不大时停止:
$$V_{\pi }(s)\leftarrow \sum _{r,s^{\prime }}P(r,s^{\prime }|s,\pi (s))\cdot [r+\gamma v_{\pi }(s^{\prime })]$$
其中$P(r,s^{\prime }|s,\pi (s))$表示在状态$s$时执行了以概率$\pi (s)$的可能性执行了某一动作$a$, 产生了状态$s^{\prime }$和奖励$r$的概率.

②策略提升: 根据①策略评估:求得的上一轮策略${\pi }_{k-1}(a│s)$下的状态价值$V_{\pi }(s)$表, 根据贪心策略更新此轮的策略$\pi (a│s)$ (即在不同的状态s时, 采取最大化$V_{\pi }(s)$的动作$a$):
$$\pi (a│s)\leftarrow argma{x}_a[V_{\pi }(s^{\prime })]$$
直到该轮策略${\pi }_k(a│s)$与上一轮的该策略${\pi }_{k-1}(a│s)$变化不大时退出全部训练, 否则就回到①继续进行策略评估:来估计当前策略下${\pi }_k(a│s)$的全部状态$s$的$V_{\pi }(s)$.

当策略$\pi (a│s)$变化不大时, 就返回当前的$\pi (a│s)$.

---

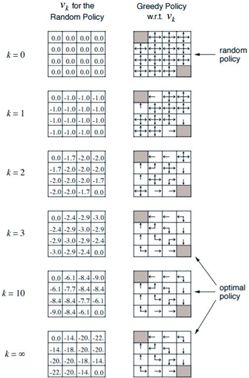图1. 基于Grid World环境的策略迭代过程: 每次迭代右图为$V_{\pi }(s)$, 左图为本次迭代生成的策略$\pi (a│s)$

举例: Grid World 是一个4x4的16宫格, 左上角和右下角的格子是终止格子. 该位置的价值固定为0, 智能体如果到达了终止格子则停止移动且此后每轮奖励都是0.
环境定义: 智能体在16宫格其他格的每次移动, 得到的即时奖励$R$都是-1. 智能体每次只能移动一个格子, 且只能(上/下/左/右)4种移动选择. 如果在边界格往外走, 则会直接移动回到之前的边界格. 设折扣因子为$\gamma =1$.
由于每次移动(上/下/左/右)下一格都是固定的, 因此执行一个动作(上/下/左/右)后, 状态转化概率是确定的$P=1$(即执行了向下的动作, 则智能体到下一个格子的概率为P=1).因为设定$P(r,s^{\prime }│s)=1$, 则只有概率$\pi (s)$起作用, 即$P(r,s^{\prime }│s,\pi (a|s))=\pi (a|s)$

设初始策略是随机策略, 即每个格子(状态$s$)里有$\pi (a│s)=1/4$的概率(上/下/左/右)向周围的4个格子移动. 并初始化所有状态$s$的状态价值$V_{\pi }(s)$为0. 由于终止格子的价值固定为0, 所以可以不将其加入迭代过程.

①策略评估: 在迭代次数k=1的时候, 利用贝尔曼方程$V_{\pi }(s)\leftarrow {\sum }_{r,s^{\prime }}P(r,s^{\prime }|s,\pi (s))\cdot [r+\gamma V_{\pi }(s^{\prime })]$计算每一个状态$s$(格子)对于的$V_{\pi }(s)$, 如$k=1$轮迭代时, 第二行第一个格子的$V_{\pi }(s)$:
$$v_{k=1}^{21}=1/4[(-1+0)+(-1+0)+(-1+0)+(-1+0)]=-1$$
第二行第二个格子的价值$V_{\pi }(s)$是:
$$v_{k=1}^{22}=1/4[(-1+0)+(-1+0)+(-1+0)+(-1+0)]=-1$$
以此类推, 计算出$k=1$全部状态的$V_{\pi }(s)$, 结果如图中$k=1$右图所示.

②策略提升: 根据①策略评估中计算出来的全部$V_{\pi }(s)$, 改进策略$\pi (a│s)$. 改进的方法就是让智能体在状态$s$时(某处格子), 选取动作的方式$\pi (a│s)$是最大化$V_{\pi }(s^{\prime })$:
$$\pi (a│s)\leftarrow argma{x}_a[V_{\pi }(s^{\prime })]$$
本次策略提升完成后的最终结果策略$\pi (a│s)$如$k=1$时的左图所示.

再次进行$k=2,3,\dots$的迭代①策略评估+②策略提升, 直到策略$\pi (a│s)$变化不大为止.

价值迭代:

价值迭代(Value Iteration)可以理解为是策略迭代的一个改进版本. 价值迭代算法是一种直接求解最优策略的方法.
其算法思想是: 在每一个状态$s$下, 依次执行每一个可能的动作$a$, 算出执行每一个动作$a$后的动作价值$Q_{\pi }(s,a)$, 从中取出最大值作为当前状态$s$的最优状态价值$V_{\pi }^{\ast }(s)$. 重复这个过程, 直到每个状态的最优价值$V_{\pi }^{\ast }(s)$不再发生变化, 则迭代结束.

---

使用贝尔曼最优方程, 将策略改进视为值函数的改进, 每一步都求取最大的动作价值函数$Q_{\pi }(s,a)$. 具体的迭代公式为:
对于每一个状态$s$, 求出所有可能动作$a$的动作价值函数$Q_{\pi }(s,a)$, 将最大的Q作为该状态s的最优状态价值函数$V_{\pi }^{\ast }(s)$.
$$Q_{\pi }(s,a)\leftarrow r+\gamma \sum _{s^{\prime }\to 终点(\infty )}P(s^{\prime }|s,a)V_{\pi }(s^{\prime })$$
$$V_{\pi }^{\ast }(s)\leftarrow ma{x}_{a\in A}{Q}_{\pi }(s,a)$$
与策略迭代相比, 价值迭代没有等到状态价值收敛才去调整策略, 而是随着状态价值的迭代及时调整策略, 这样就大大减少了迭代的次数. 最后只要值函数达到最优, 那么策略也达到最优. 也就是说策略和价值从初始状态值函数开始同步迭代计算, 最终$V_{\pi }^{\ast }(s)$收敛, 整个过程中没有遵循任何显式策略.

最终输出的策略$\pi (a│s)$就是走最大$V_{\pi }^{\ast }(s)$的动作.

---

参考文献: 强化学习（三）用动态规划（DP）求解.