从重采样到数据合成：如何处理机器学习中的不平衡分类问题？

转自：http://www.sohu.com/a/129333346_465975

选自Analytics Vidhya

作者：Upasana Mukherjee

机器之心编译

参与：马亚雄、微胖、黄小天、吴攀

如果你研究过一点机器学习和数据科学，你肯定遇到过不平衡的类分布（imbalanced class distribution）。这种情况是指：属于某一类别的观测样本的数量显著少于其它类别。

这个问题在异常检测是至关重要的的场景中很明显，例如电力盗窃、银行的欺诈交易、罕见疾病识别等。在这种情况下，利用传统机器学习算法开发出的预测模型可能会存在偏差和不准确。

发生这种情况的原因是机器学习算法通常被设计成通过减少误差来提高准确率。所以它们并没有考虑类别的分布/比例或者是类别的平衡。

这篇指南描述了使用多种采样技术来解决这种类别不平衡问题的各种方法。本文还比较了每种技术的优缺点。最后，本文作者还向我们展示了一种让你可以创建一个平衡的类分布的方法，让你可以应用专门为此设计的集成学习技术（ensemble learning technique）。本文作者为来自 KPMG 的数据分析顾问 Upasana Mukherjee。

目录

1. 不平衡数据集面临的挑战

2. 处理不平衡数据集的方法

3. 例证

4. 结论

1. 不平衡数据集面临的挑战

当今公用事业行业面临的主要挑战之一就是电力盗窃。电力盗窃是全球第三大盗窃形式。越来越多的公用事业公司倾向于使用高级的数据分析技术和机器学习算法来识别代表盗窃的消耗模式。

然而，最大的障碍之一就是海量的数据及其分布。欺诈性交易的数量要远低于正常和健康的交易，也就是说，它只占到了总观测量的大约 1-2%。这里的问题是提高识别罕见的少数类别的准确率，而不是实现更高的总体准确率。

当面临不平衡的数据集的时候，机器学习算法倾向于产生不太令人满意的分类器。对于任何一个不平衡的数据集，如果要预测的事件属于少数类别，并且事件比例小于 5%，那就通常将其称为罕见事件（rare event）。

• 不平衡类别的实例

让我们借助一个实例来理解不平衡类别。

例子：在一个公用事业欺诈检测数据集中，你有以下数据：

总观测 = 1000

欺诈观测 = 20

非欺诈观测 = 980

罕见事件比例 = 2%

这个案例的数据分析中面临的主要问题是：对于这些先天就是小概率的异常事件，如何通过获取合适数量的样本来得到一个平衡的数据集？

• 使用标准机器学习技术时面临的挑战

面临不平衡数据集的时候，传统的机器学习模型的评价方法不能精确地衡量模型的性能。

诸如决策树和 Logistic 回归这些标准的分类算法会偏向于数量多的类别。它们往往会仅预测占数据大多数的类别。在总量中占少数的类别的特征就会被视为噪声，并且通常会被忽略。因此，与多数类别相比，少数类别存在比较高的误判率。

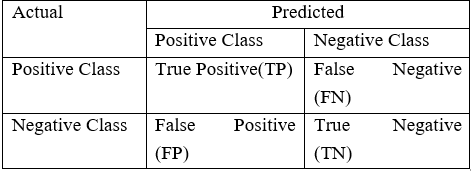
对分类算法的表现的评估是用一个包含关于实际类别和预测类别信息的混淆矩阵（Confusion Matrix）来衡量的。

如上表所示，模型的准确率 = (TP+TN) / (TP+FN+FP+TP)

然而，在不平衡领域时，准确率并不是一个用来衡量模型性能的合适指标。例如：一个分类器，在包含 2% 的罕见事件时，如果它将所有属于大部分类别的实例都正确分类，实现了 98% 的准确率；而把占 2% 的少数观测数据视为噪声并消除了。

• 不平衡类别的实例

因此，总结一下，在尝试利用不平衡数据集解决特定业务的挑战时，由标准机器学习算法生成的分类器可能无法给出准确的结果。除了欺诈性交易，存在不平衡数据集问题的常见业务问题还有：

• 识别客户流失率的数据集，其中绝大多数顾客都会继续使用该项服务。具体来说，电信公司中，客户流失率低于 2%。

• 医疗诊断中识别罕见疾病的数据集

• 自然灾害，例如地震

• 使用的数据集

这篇文章中，我们会展示多种在高度不平衡数据集上训练一个性能良好的模型的技术。并且用下面的欺诈检测数据集来精确地预测罕见事件：

总观测 = 1000

欺诈观测 = 20

非欺诈性观测 = 980

事件比例 = 2%

欺诈类别标志 = 0（非欺诈实例）

欺诈类别标志 = 1（欺诈实例）

2. 处理不平衡数据集的方法

• 2.1 数据层面的方法：重采样技术

处理不平衡数据集需要在往机器学习算法输入数据之前，制定诸如提升分类算法或平衡训练数据的类（数据预处理）的策略。后者因为应用范围广泛而更常使用。

平衡分类的主要目标不是增加少数类的的频率就是降低多数类的频率。这样做是为了获得大概相同数量的两个类的实例。让我们一起看看几个重采样（resampling）技术：

2.1.1 随机欠采样（Random Under-Sampling）

随机欠采样的目标是通过随机地消除占多数的类的样本来平衡类分布；直到多数类和少数类的实例实现平衡，目标才算达成。

总观测= 1000

欺诈性观察 = 20

非欺诈性观察 = 980

事件发生率 = 2%

这种情况下我们不重复地从非欺诈实例中取 10% 的样本，并将其与欺诈性实例相结合。

随机欠采样之后的非欺诈性观察 = 980 x 10% = 98

结合欺诈性与非欺诈性观察之后的全体观察 = 20+98 = 118

欠采样之后新数据集的事件发生率 = 20／118 = 17%

• 优点

• 它可以提升运行时间；并且当训练数据集很大时，可以通过减少样本数量来解决存储问题。

• 缺点

• 它会丢弃对构建规则分类器很重要的有价值的潜在信息。

• 被随机欠采样选取的样本可能具有偏差。它不能准确代表大多数。从而在实际的测试数据集上得到不精确的结果。

2.1.2 随机过采样（Random Over-Sampling）

过采样（Over-Sampling）通过随机复制少数类来增加其中的实例数量，从而可增加样本中少数类的代表性。

总观测= 1000

欺诈性观察 = 20

非欺诈性观察 = 980

事件发生率 = 2%

这种情况下我们复制 20 个欺诈性观察 20 次。

非欺诈性观察 = 980

复制少数类观察之后的欺诈性观察 = 400

过采样之后新数据集中的总体观察 = 1380

欠采样之后新数据集的事件发生率 = 400/1380 = 29%

• 优点

• 与欠采样不同，这种方法不会带来信息损失。

• 表现优于欠采样。

• 缺点

• 由于复制少数类事件，它加大了过拟合的可能性。

2.1.3 基于聚类的过采样（Cluster-Based Over Sampling）

在这种情况下，K-均值聚类算法独立地被用于少数和多数类实例。这是为了识别数据集中的聚类。随后，每一个聚类都被过采样以至于相同类的所有聚类有着同样的实例数量，且所有的类有着相同的大小。

总观测= 1000

欺诈性观察 = 20

非欺诈性观察 = 980

事件发生率 = 2%

• 多数类聚类

1. 聚类 1：150 个观察

2. 聚类 2：120 个观察

3. 聚类 3：230 个观察

4. 聚类 4：200 个观察

5. 聚类 5：150 个观察

6. 聚类 6：130 个观察

• 少数类聚类

1. 聚类 1：8 个观察

2. 聚类 2：12 个观察

每个聚类过采样之后，相同类的所有聚类包含相同数量的观察。

• 多数类聚类

1. 聚类 1：170 个观察

2. 聚类 2：170 个观察

3. 聚类 3：170 个观察

4. 聚类 4：170 个观察

5. 聚类 5：170 个观察

6. 聚类 6：170 个观察

• 少数类聚类

1. 聚类 1：250 个观察

2. 聚类 2：250 个观察

基于聚类的过采样之后的事件率 = 500/ (1020+500) = 33 %

• 优点

• 这种聚类技术有助于克服类之间不平衡的挑战。表示正例的样本数量不同于表示反例的样本数量。

• 有助于克服由不同子聚类组成的类之间的不平衡的挑战。每一个子聚类不包含相同数量的实例。

• 缺点

• 正如大多数过采样技术，这一算法的主要缺点是有可能过拟合训练集。

2.1.4 信息性过采样：合成少数类过采样技术（SMOTE）

这一技术可用来避免过拟合——当直接复制少数类实例并将其添加到主数据集时。从少数类中把一个数据子集作为一个实例取走，接着创建相似的新合成的实例。这些合成的实例接着被添加进原来的数据集。新数据集被用作样本以训练分类模型。

总观测= 1000

欺诈性观察 = 20

非欺诈性观察 = 980

事件发生率 = 2%

从少数类中取走一个包含 15 个实例的样本，并生成相似的合成实例 20 次。

生成合成性实例之后，创建下面的数据集

少数类（欺诈性观察）= 300

多数类（非欺诈性观察）= 980

事件发生率 = 300/1280 = 23.4 %

• 优点

• 通过随机采样生成的合成样本而非实例的副本，可以缓解过拟合的问题。

• 不会损失有价值信息。

• 缺点

• 当生成合成性实例时，SMOTE 并不会把来自其他类的相邻实例考虑进来。这导致了类重叠的增加，并会引入额外的噪音。

• SMOTE 对高维数据不是很有效。

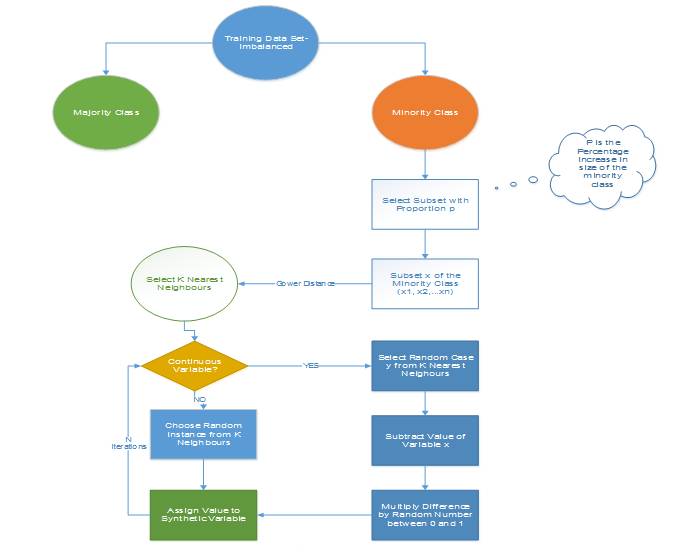
图 1：合成少数类过采样算法，其中 N 是属性的数量

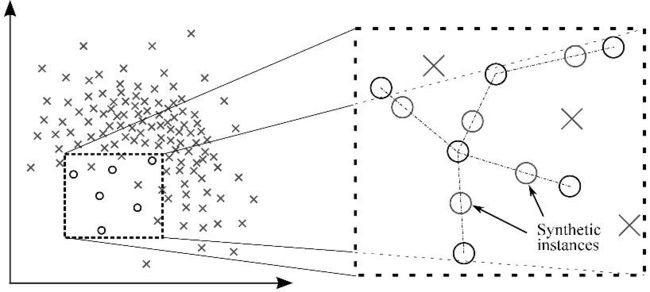
图 2：借助 SMOTE 的合成实例生成

2.15 改进的合成少数类过采样技术（MSMOTE）

这是 SMOTE 的改进版本，SMOTE 没有考虑数据集中少数类和潜在噪声的基本分布。所以为了提高 SMOTE 的效果，MSMOTE 应运而生。

该算法将少数类别的样本分为 3 个不同的组：安全样本、边界样本和潜在噪声样本。分类通过计算少数类的样本和训练数据的样本之间的距离来完成。安全样本是可以提高分类器性能的那些数据点。而另一方面，噪声是可以降低分类器的性能的数据点。两者之间的那些数据点被分类为边界样本。

虽然 MSOMTE 的基本流程与 SMOTE 的基本流程相同，在 MSMOTE 中，选择近邻的策略不同于 SMOTE。该算法是从安全样本出发随机选择 k-最近邻的数据点，并从边界样本出发选择最近邻，并且不对潜在噪声样本进行任何操作。

• 2.2 算法集成技术（Algorithmic Ensemble Techniques）

上述部分涉及通过重采样原始数据提供平衡类来处理不平衡数据，在本节中，我们将研究一种替代方法：修改现有的分类算法，使其适用于不平衡数据集。

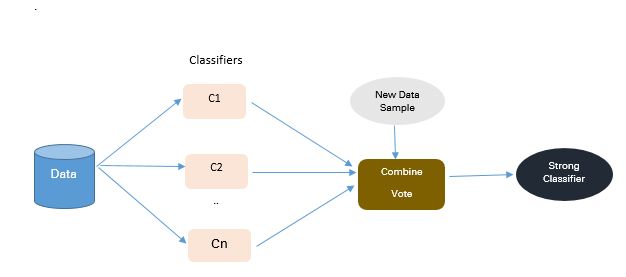
集成方法的主要目的是提高单个分类器的性能。该方法从原始数据中构建几个两级分类器，然后整合它们的预测。

图 3：基于集成的方法

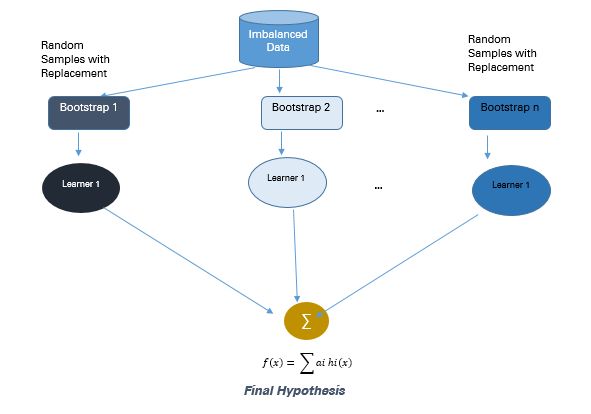
2.2.1 基于 Bagging 的方法

Bagging 是 Bootstrap Aggregating 的缩写。传统的 Bagging 算法包括生成「n」个不同替换的引导训练样本，并分别训练每个自举算法上的算法，然后再聚合预测。

Bagging 常被用于减少过拟合，以提高学习效果生成准确预测。与 boosting 不同，bagging 方法允许在自举样本中进行替换。

图 4：Bagging 方法

总观测= 1000

欺诈观察= 20

非欺诈观察= 980

事件率= 2％

从具有替换的群体中选择 10 个自举样品。每个样本包含 200 个观察值。每个样本都不同于原始数据集，但类似于分布和变化上与该数据集类似。机器学习算法（如 logistic 回归、神经网络与决策树）拟合包含 200 个观察的自举样本，且分类器 c1，c2 ... c10 被聚合以产生复合分类器。这种集成方法能产生更强的复合分类器，因为它组合了各个分类器的结果。

• 优点

• 提高了机器学习算法的稳定性与准确性

• 减少方差

• 减少了 bagged 分类器的错误分类

• 在嘈杂的数据环境中，bagging 的性能优于 boosting

• 缺点

• bagging 只会在基本分类器效果很好时才有效。错误的分类可能会进一步降低表现。

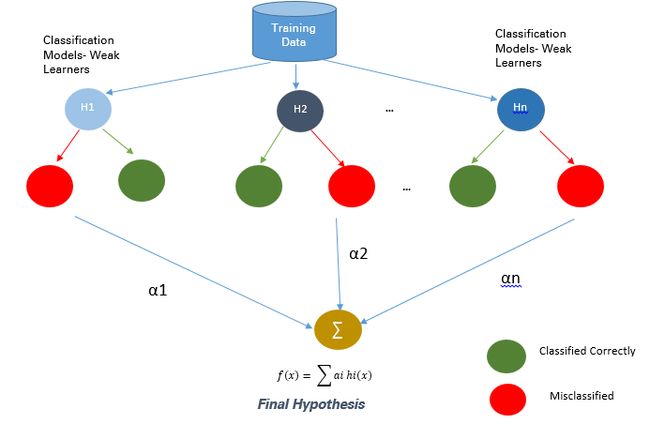
2.2.2. 基于 Boosting 的方法

Boosting 是一种集成技术，它可以将弱学习器结合起来创造出一个能够进行准确预测的强大学习器。Boosting 开始于在训练数据上准备的基本分类器/弱分类器。

基本学习器/分类器是弱学习器，即预测准确度仅略好于平均水平。弱是指当数据的存在小变化时，会引起分类模型出现大的变化。

在下一次迭代中，新分类器将重点放在那些在上一轮中被错误分类的案例上。

图 5：Boosting 方法

2.2.2.1 自适应 boosting——Ada Boost

Ada Boost 是最早的 boosting 技术，其能通过许多弱的和不准确的规则的结合来创造高准确度的预测。其中每个训练器都是被串行地训练的，其目标在每一轮正确分类上一轮没能正确分类的实例。

对于一个学习过的分类器，如果要做出强大的预测，其应该具备以下三个条件：

• 规则简单

• 分类器在足够数量的训练实例上进行了训练

• 分类器在训练实例上的训练误差足够低

每一个弱假设都有略优于随机猜测的准确度，即误差项 € (t) 应该略大约 ½-β，其中 β>0。这是这种 boosting 算法的基础假设，其可以产生一个仅有一个很小的误差的最终假设。

在每一轮之后，它会更加关注那些更难被分类的实例。这种关注的程度可以通过一个权重值（weight）来测量。起初，所有实例的权重都是相等的，经过每一次迭代之后，被错误分类的实例的权重会增大，而被正确分类的实例的权重则会减小。

图 6：自适应 boosting 的方法

比如如果有一个包含了 1000 次观察的数据集，其中有 20 次被标记为了欺诈。刚开始，所有的观察都被分配了相同的权重 W1，基础分类器准确分类了其中 400 次观察。

然后，那 600 次被错误分类的观察的权重增大为 W2，而这 400 次被正确分类的实例的权重减小为 W3。

在每一次迭代中，这些更新过的加权观察都会被送入弱的分类器以提升其表现。这个过程会一直持续，直到错误分类率显著降低，从而得到一个强大的分类器。

• 优点

• 非常简单就能实现

• 可以很好地泛化——适合任何类型的分类问题且不易过拟合

• 缺点

• 对噪声数据和异常值敏感

2.2.2.2 梯度树 boosting

在梯度 Boosting（Gradient Boosting）中，许多模型都是按顺序训练的。其是一种数值优化算法，其中每个模型都使用梯度下降（Gradient Descent）方法来最小化损失函数 y = ax+b+e。

在梯度 Boosting 中，决策树（Decision Tree）被用作弱学习器。

尽管 Ada Boost 和梯度 Boosting 都是基于弱学习器/分类器工作的，而且都是在努力使它们变成强大的学习器，但这两种方法之间存在一些显著的差异。Ada Boost 需要在实际的训练过程之前由用户指定一组弱学习器或随机生成弱学习器。其中每个学习器的权重根据其每步是否正确执行了分类而进行调整。而梯度 Boosting 则是在训练数据集上构建第一个用来预测样本的学习器，然后计算损失（即真实值和第一个学习器的输出之间的差），然后再使用这个损失在第二个阶段构建改进了的学习器。

在每一个步骤，该损失函数的残差（residual）都是用梯度下降法计算出来的，而新的残差会在后续的迭代中变成目标变量。

梯度 Boosting 可以通过 R 语言使用 SAS Miner 和 GBM 软件包中的 Gradient Boosting Node 实现。

图 7：梯度 Boosting 方法

比如，如果有一个包含了 1000 次观察的训练数据集，其中有 20 次被标记为了欺诈，并且还有一个初始的基础分类器。目标变量为 Fraud，当交易是欺诈时，Fraud=1；当交易不是欺诈时，Fraud=0.

比如说，决策树拟合的是准确分类仅 5 次观察为欺诈观察的情况。然后基于该步骤的实际输出和预测输出之间的差，计算出一个可微的损失函数。该损失函数的这个残差是下一次迭代的目标变量 F1。

类似地，该算法内部计算该损失函数，并在每个阶段更新该目标，然后在初始分类器的基础上提出一个改进过的分类器。

• 缺点

• 梯度增强过的树比随机森林更难拟合

• 梯度 Boosting 算法通常有 3 个可以微调的参数：收缩（shrinkage）参数、树的深度和树的数量。要很好拟合，每个参数都需要合适的训练。如果这些参数没有得到很好的调节，那么就可能会导致过拟合。

2.2.2.3 XGBoost

XGBoost（Extreme Gradient Boosting/极限梯度提升）是 Gradient Boosting 算法的一种更先进和更有效的实现。

相对于其它 Boosting 技术的优点：

• 速度比普通的 Gradient Boosting 快 10 倍，因为其可以实现并行处理。它是高度灵活的，因为用户可以自定义优化目标和评估标准，其具有内置的处理缺失值的机制。

• 和遇到了负损失就会停止分裂节点的 Gradient Boosting 不同，XGBoost 会分裂到指定的最大深度，然后会对其树进行反向的剪枝（prune），移除仅有一个负损失的分裂。

XGBoost 可以使用 R 和 Python 中的 XGBoost 包实现。

3. 实际案例

• 3.1 数据描述

这个例子使用了电信公司的包含了 47241 条顾客记录的数据集，每条记录包含的信息有 27 个关键预测变量

罕见事件数据集的数据结构如下，缺失值删除、异常值处理以及降维

从这里下载数据集：https://static.analyticsvidhya.com/wp-content/uploads/2017/03/17063705/SampleData_IMC.csv

• 3.2 方法描述

使用合成少数类过采样技术（SMOTE）来平衡不平衡数据集——该技术是试图通过创建合成实例来平衡数据集。下面以 R 代码为例，示范使用 Gradient Boosting 算法来训练平衡数据集。

R 代码

# 加载数据

rareevent_boost <- read.table("D:/Upasana/RareEvent/churn.txt",sep="|", header=TRUE)dmy<-dummyVars("~.",data=rareevent_boost)rareeventTrsf<-data.frame(predict(dmy,newdata= rareevent_boost))set.seed(10)sub <- sample(nrow(rareeventTrsf), floor(nrow(rareeventTrsf) * 0.9))sub1 <- sample(nrow(rareeventTrsf), floor(nrow(rareeventTrsf) * 0.1))training <- rareeventTrsf [sub, ]testing <- rareeventTrsf [-sub, ]training_sub<- rareeventTrsf [sub1, ]tables(training_sub)head(training_sub)

# 对于不平衡的数据集 #

install.packages("unbalanced")library(unbalanced)data(ubIonosphere)n<-ncol(rareevent_boost)output<- rareevent_boost $CHURN_FLAGoutput<-as.factor(output)input<- rareevent_boost [ ,-n]View(input)

# 使用 ubSMOTE 来平衡数据集 #

data<-ubBalance(X= input, Y=output, type="ubSMOTE", percOver=300, percUnder=150, verbose=TRUEView(data)

# 平衡的数据集 #

balancedData<-cbind(data$X,data$Y)View(balancedData)table(balancedData$CHURN_FLAG)

# 写入平衡的数据集来训练模型 #

write.table(balancedData,"D:/ Upasana/RareEvent /balancedData.txt", sep="t", row.names=FALSE)

# 创建 Boosting 树模型 #

repalceNAsWithMean <- function(x) {replace(x, is.na(x), mean(x[!is.na(x)]))}training <- repalceNAsWithMean(training)testing <- repalceNAsWithMean(testing)

# 重采样技术 #

View(train_set)fitcontrol<-trainControl(method="repeatedcv",number=10,repeats=1,verbose=FALSE)gbmfit<-train(CHURN_FLAG~.,data=balancedData,method="gbm",verbose=FALSE)

# 为测试数据评分 #

testing$score_Y=predict(gbmfit,newdata=testing,type="prob")[,2]testing$score_Y=ifelse(testing$score_Y>0.5,1,0)head(testing,n=10)write.table(testing,"D:/ Upasana/RareEvent /testing.txt", sep="t", row.names=FALSE)pred_GBM<-prediction(testing$score_Y,testing$CHURN_FLAG)

# 模型的表现 #

model_perf_GBM <- performance(pred_GBM, "tpr", "fpr")model_perf_GBM1 <- performance(pred_GBM, "tpr", "fpr")model_perf_GBMpred_GBM1<-as.data.frame(model_perf_GBM)auc.tmp_GBM <- performance(pred_GBM,"auc")AUC_GBM <- as.numeric([email protected])auc.tmp_GBM

• 结果

这个在平衡数据集上使用了 SMOTE 并训练了一个 gradient boosting 算法的平衡数据集的办法能够显著改善预测模型的准确度。较之平常分析建模技术（比如 logistic 回归和决策树），这个办法将其 lift 提升了 20%，精确率也提升了 3 到 4 倍。

4. 结论

遇到不平衡数据集时，没有改善预测模型准确性的一站式解决方案。你可能需要尝试多个办法来搞清楚最适合数据集的采样技术。在绝大多数情况下，诸如 SMOTE 以及 MSMOTE 之类的合成技术会比传统过采样或欠采样的办法要好。

为了获得更好的结果，你可以在使用诸如 Gradeint boosting 和 XGBoost 的同时也使用 SMOTE 和 MSMOTE 等合成采样技术。

通常用于解决不平衡数据集问题的先进 bagging 技术之一是 SMOTE bagging。这个办法采取了一种完全不同于传统 bagging 技术的办法来创造每个 Bag/Bootstrap。通过每次迭代时设置一个 SMOTE 重采样率，它可以借由 SMOTE 算法生成正例。每次迭代时，负例集会被 bootstrap。

不平衡数据集的特点不同，最有效的技术也会有所不同。对比模型时要考虑相关评估参数。

在对比通过全面地结合上述技术而构建的多个预测模型时，ROC 曲线下的 Lift & Area 将会在决定最优模型上发挥作用。

参考文献

1. Dmitry Pavlov, Alexey Gorodilov, Cliff Brunk「BagBoo: A Scalable Hybrid Bagging-theBoosting Model」.2010

2. Fithria Siti Hanifah , Hari Wijayanto , Anang Kurnia「SMOTE Bagging Algorithm for Imbalanced Data Set in Logistic Regression Analysis」. Applied Mathematical Sciences, Vol. 9, 2015

3. Lina Guzman, DIRECTV「Data sampling improvement by developing SMOTE technique in SAS」.Paper 3483-2015

4. Mikel Galar, Alberto Fern´andez, Edurne Barrenechea, Humberto Bustince and Francisco Herrera「A Review on Ensembles for the Class Imbalance Problem: Baggng-, Boosting-, and Hybrid-Based Approaches」.2011 IEEE

原文地址：https://www.analyticsvidhya.com/blog/2017/03/imbalanced-classification-problem