《Java数据结构》——优先级队列(小根堆的模拟实现)
目录
引子
一、堆的概念
二、堆的性质
三、堆的操作
向下调整算法
小根堆的创建
向上调整算法
堆的插入
堆的删除(堆顶元素的删除)
四、优先级队列的模拟实现(小根堆)
引子
我们之前学过队列,那么什么是优先级队列呢?
举个例子
队列是一种先进先出(FIFO)的数据结构,但是有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,在这种情况下使用队列就不行了,比如玩游戏的时候突然女朋友一通电话,游戏屏幕瞬间被电话占领,这时候就应该优先处理电话。
在这种情况下,我们的数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新对象,这种数据结构就是优先级队列(PriorityQueue)。
但其实这种对优先级队列的定义是不严谨的,严谨的说法是
- 优先级队列是逻辑结构是小根堆,存储结构是动态数组(到达上限,容量自动加一)的集合类。
- 所以说优先级队列不是数据结构中的概念,而是java中的集合类。
- 但在JDK1.8中的PriorityQueue底层使用了堆的数据结构,而堆实际就是在完全二叉树的基础之上进行了一些元素的调整,所以说优先级队列是一种数据结构也未尝不可
既然优先级队列的底层用到了堆这种数据结构,那么什么是堆呢?
一、堆的概念
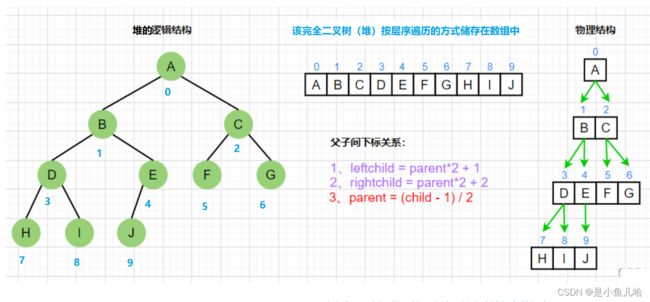
前提知识:二叉树的顺序存储
使用数组存储二叉树的方式,就是将二叉树按照层序遍历放入数组
一般只适合完全二叉树,因为非完全二叉树会有空间的浪费
而堆其实就是一棵完全二叉树,所以就可以用数组来储存堆这一数据结构
概括:堆就是一颗顺序存储的完全二叉树,底层是一个数组
-
堆逻辑上是一颗完全二叉树
-
堆物理上是保存在数组中
二、堆的性质
既然是完全二叉树,那么之前我们得出来的那些完全二叉树的性质也同样适用于堆
下面是一个完全二叉树,也同样是一个堆
也就是说已知父亲结点的下标就能求出孩子结点的下标,同理如果知道了孩子结点的下标也能求出他所对应的父亲结点的下标
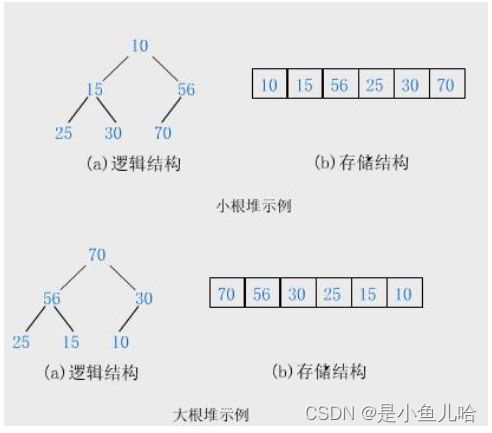
堆分两种:大根堆和小根堆
- 小根堆:每一个父结点的值均小于等于其对应的子结点的值,而根结点的值就是最小的。
- 大根堆:每一个父结点的值均大于等于其对应的子结点的值,而根结点的值就是最大的。
如此一来我们就又得到了堆的另外两条性质
- 堆中某个节点的值总是不大于或不小于其父节点的值。
- 堆总是一棵完全二叉树。
- 但完全二叉树不一定能称作堆(可能无序,不满足堆的性质)
三、堆的操作
向下调整算法
此时我们看到,这个二叉树整体上不符合堆的性质,但是其根部的左子树和右子树均满足堆的性质。
注意上面说的也是向下调整的前提即——必须得确保根结点的左右子树均为小堆才可
接下来,就要进行向下调整,确保其最终是个堆。只需三步。
- 找出左右孩子中最小的那个
- 跟父亲比较,如果比父亲小,就交换
- 更新父亲结点(继续向下调整,因为经过上一次调整后下面的子树可能就不满足小根堆的性质了)
调整过程如图所示
你可能问会问:你是怎样得到父亲结点和他所对应的孩子结点的位置的,不就是根据完全二叉树的性质呀!
左孩子结点的下标 = (2 * 父亲结点的下标 + 1)
右孩子结点的下标 = (2 * 父亲结点的下标 + 2)
父亲结点的下标 = (孩子结点的下标 - 1) / 2
但要注意我们的数组长度是有限的,表示孩子结点的下标不能超过数组所允许的最大下标
所以说,只要我们一开始给出要调整的二叉树的根节点坐标(父亲结点坐标),我们就能将给定的这棵完全二叉树变成小根堆
代码如下:
/**
* 向下调整——使得当前子树为小根堆
* @param root 是每棵子树的根结点的下标
* 向下调整的时间复杂度O(log2n)(最坏情况下就是树的高度)
*/
public void shiftDown(int root) {
int parent = root; // 父亲结点的坐标
int child = 2 * parent + 1; // 获取左孩子结点的坐标
// 为什么不能child下标要小于usedSize,因为当前数组的最大下标就是usedSize - 1,如果大于或等于usedSize就越界了
while (child < usedSize) { // 每个子树在调整的时候,是按从上到下,当child的下标小于usedSize时候就结束
// 这一步目的是找出孩子结点最大的那个值,然后在让该值和父亲结点比较(不过先要确定孩子结点存在)
if (child + 1 < usedSize && elem[child] > elem[child + 1]) {
child = child + 1;
}
if (elem[child] < elem[parent]) {
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
parent = child; // 从上向下调整子树,更新父亲结点的下标
child = 2 * parent + 1; // 更新左孩子孩子结点的下标
}
// 因为我们是从上向下调整子树,当我们在调整上面的子树时,下面的子树一定是调整好了的,如果上面都已经满足小根堆,下面也一定满足
else {
break; // 此时已经是小根堆了,不需要再次调整,直接退出循环接着调整下一个子树
}
}
}
小根堆的创建
声明一下:我们通常所用到的堆,要么是小根堆、要么就是大根堆,这里我们所创建的就一个小根堆
既然说堆是一种可以用数组来储存,那么如果给了一个无序的数组,怎样把他变成一个有序的小根堆(完全二叉树)呢?
我们是不是就应该在创建的过程中,及时的调整数组中的元素位置,让该堆成为一个小根堆(根结点的值大于左右孩子结点的值)
比如这样一个数组
那该怎么调整呢?
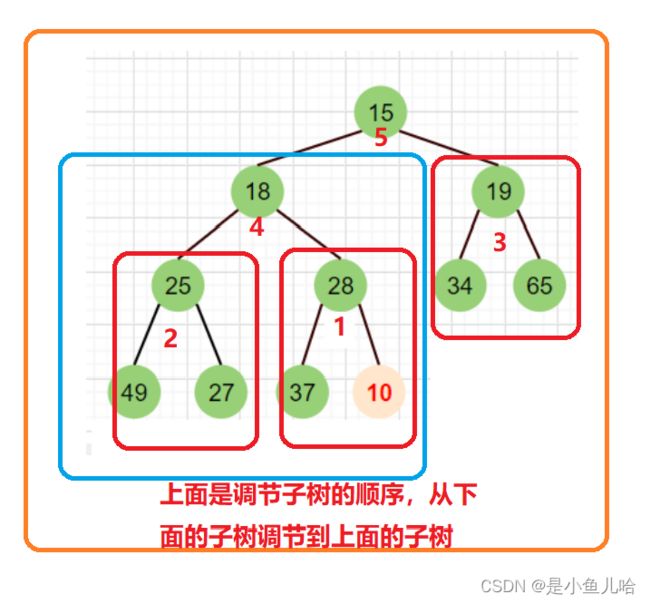
好像每一个子树都不符合小根堆的定义啊!那么我们就需要从从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,这样从上到下调整不同的子树后就可以调整成堆
至于每个子树的调节方式,那不就是我们刚才提到的从根结点开始对指定的子树进行向下调节吗
为什么要从下面的较小的子树调节到上面的大子树?
这是因为我们刚才的向下调整法,所能作用的二叉树是:整体上不符合堆的性质,但是其根部的左子树和右子树均满足堆的性质
当我们从上向下进行调节时,即从倒数的第一个非叶子节点的子树开始调节时,此时的二叉树一定是满足这个性质的,当下面的子树调节好了后,你会发现此时原来不满足这个性质的上面的那些子树竟然也满足这些性质了(因为他下面的子树已经调节过了)
思路如下图所示(这里是虽然构建的是大堆根,但思路是一样的):
代码如下:
public class MyHeap {
int[] elem; // 我们说过堆可以用数组来存放
int usedSize; // 优先级队列中有效元素的个数
MyHeap() {
elem = new int[10]; // 构造方法初始化一下,堆(数组)的容量
}
public void createHeap(int[] arrays) {
for (int i = 0; i < arrays.length; i++) {
elem[i] =arrays[i]; // 元素初始化,给堆中元素赋值
++usedSize;
}
// 倒数的第一个非叶子节点的子树开始调节,一直调节到根结点(根节点在数组中的下标为0)
// 注意这里是usdSize - 1 - 1,因为父亲结点的下标 = (孩子结点的下标 - 1) / 2,
// 我们是从倒数的第一个非叶子节点的子树开始调节的,而该子树的孩子结点坐标为usedSize - 1
for (int i = (usedSize - 1 - 1) / 2; i >= 0 ; --i) {
shiftDown(i); // 从下面的子树一直调到上面的子树
}
}
/**
* 向下调整——使得当前子树为小根堆
* @param root 是每棵子树的根结点的下标
* 向下调整的时间复杂度O(log2n)(最坏情况下就是树的高度)
*/
public void shiftDown(int root) {
int parent = root; // 父亲结点的坐标
int child = 2 * parent + 1; // 获取左孩子结点的坐标
// 为什么不能child下标要小于usedSize,因为当前数组的最大下标就是usedSize - 1,如果大于或等于usedSize就越界了
while (child < usedSize) { // 每个子树在调整的时候,是按从上到下,当child的下标小于usedSize时候就结束
// 这一步目的是找出孩子结点最大的那个值,然后在让该值和父亲结点比较(不过先要确定孩子结点存在)
if (child + 1 < usedSize && elem[child] > elem[child + 1]) {
child = child + 1;
}
if (elem[child] < elem[parent]) {
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
parent = child; // 从上向下调整子树,更新父亲结点的下标
child = 2 * parent + 1; // 更新左孩子孩子结点的下标
}
// 因为我们是从上向下调整子树,当我们在调整上面的子树时,下面的子树一定是调整好了的,如果上面都已经满足小根堆,下面也一定满足
else {
break; // 此时已经是小根堆了,不需要再次调整,直接退出循环接着调整下一个子树
}
}
}
}
向上调整算法
我们由堆的插入引入该算法
堆的插入不像先前顺序表一般,可以头插,任意位置插入等等,因为是堆,要符合大根堆或小根堆的性质,不能改变堆原本的结构,所以尾插才是最适合的,并且尾插后还要检查是否符合堆的性质。
为了确保在插入数字10后依然是个小根堆,所以要将10和28交换,依次比较父结点parent和子结点child的大小,当父小于子结点的时候,就返回,反之就一直交换,直到根部。
由前文的得知的规律,parent = (child - 1) / 2,我们可以从下到上调整子树,不断的更新child和parent下标,直到根部15
需要注意的是:我们操控的是数组,但要把它想象成二叉树。画图演示调整过程:
![]()
这就是向上调整算法
代码如下:
/**
* 从下向上调整子树
* @param child 要调整子树的孩子坐标
*/
public void shiftUp(int child) {
int parent = (child - 1) / 2; // 通过孩子坐标得出父亲坐标
while (child > 0) { // 当孩子坐标等于0时,说明根结点已经调整完毕,退出循环
// 因为之前的该子树的孩子结点的值肯定满足小根堆,所以我们只用考虑新加入的孩子结点的值
if (elem[parent] > elem[child]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
// 更新
child = parent;
parent = (child - 1) / 2;
}
else {
break; // 因为我们是从下向上调整子树的,我们上面的结点之前是满足小根堆的,所以如果下面也满足了,说明整个子树都满足了,直接退出循环
}
}
}堆的插入
讲完了说完了向上调整算法,那堆的插入不就很简单了吗!
代码如下:
/**
* 入队,当要保证入队后仍是小根堆
* @param val 要入队的元素
*/
public void offerHeap(int val) {
if (isFull()) {
elem = new int[2 * usedSize];
}
else {
elem[usedSize] = val; // 把新添加的元素放到数组中最后的位置
++usedSize;
shiftUp(usedSize - 1); // 放完后就从新元素的位置——从下向上调整该子树
}
}
/**
* 从下向上调整子树
* @param child 要调整子树的孩子坐标
*/
public void shiftUp(int child) {
int parent = (child - 1) / 2; // 通过孩子坐标得出父亲坐标
while (child > 0) { // 当孩子坐标等于0时,说明根结点已经调整完毕,退出循环
// 因为之前的该子树的孩子结点的值肯定满足小根堆,所以我们只用考虑新加入的孩子结点的值
if (elem[parent] > elem[child]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
// 更新
child = parent;
parent = (child - 1) / 2;
}
else {
break; // 因为我们是从下向上调整子树的,我们上面的结点之前是满足小根堆的,所以如果下面也满足了,说明整个子树都满足了,直接退出循环
}
}
}
// 判断当前队列是否已满
public boolean isFull() {
return usedSize == elem.length;
}堆的删除(堆顶元素的删除)
堆的删除和堆的插入很相似,就是把要删除的根节点和堆的最后一个元素互换位置,然后从上向下调整子树:
- 将堆顶元素对堆中最后一个元素交换
- 将堆中有效数据个数减少一个
- 对堆顶元素进行向下调整
举个栗子
删除过程如下
代码如下:
/**
* 出队删除,每次删除的都是优先级高的元素——当前完全二叉树的根结点
* 出队后仍要保证该二叉树是小根堆
*/
public void pollHeap() {
if (isEmpty()) {
System.out.println("当前优先级队列为空!");
return;
}
// 将当前的队首元素与队尾元素互换位置,然后将向下调整以队首元素为根节点的那个子树,使得满小根堆
int tmp = elem[usedSize - 1];
elem[usedSize - 1] = elem[0];
elem[0] = tmp;
--usedSize; // 既然是删除,有效元素个数要减一
shiftDown(0);
}
/**
* 向下调整——使得当前子树为小根堆
* @param root 是每棵子树的根结点的下标
* 向下调整的时间复杂度O(log2n)(最坏情况下就是树的高度)
*/
public void shiftDown(int root) {
int parent = root; // 父亲结点的坐标
int child = 2 * parent + 1; // 获取左孩子结点的坐标
// 为什么不能child下标要小于usedSize,因为当前数组的最大下标就是usedSize - 1,如果大于或等于usedSize就越界了
while (child < usedSize) { // 每个子树在调整的时候,是按从上到下,当child的下标小于usedSize时候就结束
// 这一步目的是找出孩子结点最大的那个值,然后在让该值和父亲结点比较(不过先要确定孩子结点存在)
if (child + 1 < usedSize && elem[child] > elem[child + 1]) {
child = child + 1;
}
if (elem[child] < elem[parent]) {
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
parent = child; // 从上向下调整子树,更新父亲结点的下标
child = 2 * parent + 1; // 更新左孩子孩子结点的下标
}
// 因为我们是从上向下调整子树,当我们在调整上面的子树时,下面的子树一定是调整好了的,如果上面都已经满足小根堆,下面也一定满足
else {
break; // 此时已经是小根堆了,不需要再次调整,直接退出循环接着调整下一个子树
}
}
}
// 判断当前优先级队列是否为空
public boolean isEmpty() {
return usedSize == 0;
}四、优先级队列的模拟实现(小根堆)
到了这里,相信大家对小根堆的各自操作应该已经不陌生了吧!那么接下来就让我们用这些操作模拟实现一个优先级队列
/**
* 用小根堆模拟实现优先级队列
*/
public class MyHeap {
int[] elem;
int usedSize; // 优先级队列中有效元素的个数
MyHeap() {
elem = new int[10]; // 构造方法初始化一下
}
public void createHeap(int[] arrays) {
for (int i = 0; i < arrays.length; i++) {
elem[i] =arrays[i]; // 元素初始化
++usedSize;
}
for (int i = (usedSize - 1) / 2; i >= 0 ; --i) {
shiftDown(i); // 从下面的子树一直调到上面的子树
}
}
/**
* 向下调整——使得当前子树为小根堆
* @param root 是每棵子树的根结点的下标
* 向下调整的时间复杂度O(log2n)(最坏情况下就是树的高度)
*/
public void shiftDown(int root) {
int parent = root; // 父亲结点的坐标
int child = 2 * parent + 1; // 获取左孩子结点的坐标
// 为什么不能child下标要小于usedSize,因为当前数组的最大下标就是usedSize - 1,如果大于或等于usedSize就越界了
while (child < usedSize) { // 每个子树在调整的时候,是按从上到下,当child的下标小于usedSize时候就结束
// 这一步目的是找出孩子结点最大的那个值,然后在让该值和父亲结点比较(不过先要确定孩子结点存在)
if (child + 1 < usedSize && elem[child] > elem[child + 1]) {
child = child + 1;
}
if (elem[child] < elem[parent]) {
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
parent = child; // 从上向下调整子树,更新父亲结点的下标
child = 2 * parent + 1; // 更新左孩子孩子结点的下标
}
// 因为我们是从上向下调整子树,当我们在调整上面的子树时,下面的子树一定是调整好了的,如果上面都已经满足小根堆,下面也一定满足
else {
break; // 此时已经是小根堆了,不需要再次调整,直接退出循环接着调整下一个子树
}
}
}
/**
* 入队,当要保证入队后仍是小根堆
* @param val 要入队的元素
*/
public void offerHeap(int val) {
if (isFull()) {
elem = new int[2 * usedSize];
}
else {
elem[usedSize] = val; // 把新添加的元素放到数组中最后的位置
++usedSize;
shiftUp(usedSize - 1); // 放完后就从新元素的位置——从下向上调整该子树
}
}
/**
* 从下向上调整子树
* @param child 要调整子树的孩子坐标
*/
public void shiftUp(int child) {
int parent = (child - 1) / 2; // 通过孩子坐标得出父亲坐标
while (child > 0) { // 当孩子坐标等于0时,说明根结点已经调整完毕,退出循环
// 因为之前的该子树的孩子结点的值肯定满足小根堆,所以我们只用考虑新加入的孩子结点的值
if (elem[parent] > elem[child]) {
int tmp = elem[parent];
elem[parent] = elem[child];
elem[child] = tmp;
// 更新
child = parent;
parent = (child - 1) / 2;
}
else {
break; // 因为我们是从下向上调整子树的,我们上面的结点之前是满足小根堆的,所以如果下面也满足了,说明整个子树都满足了,直接退出循环
}
}
}
// 判断当前队列是否已满
public boolean isFull() {
return usedSize == elem.length;
}
/**
* 出队删除,每次删除的都是优先级高的元素——当前完全二叉树的根结点
* 出队后仍要保证该二叉树是小根堆
*/
public void pollHeap() {
if (isEmpty()) {
System.out.println("当前优先级队列为空!");
return;
}
// 将当前的队首元素与队尾元素互换位置,然后将向下调整以队首元素为根节点的那个子树,使得满小根堆
int tmp = elem[usedSize - 1];
elem[usedSize - 1] = elem[0];
elem[0] = tmp;
--usedSize; // 既然是删除,有效元素个数要减一
shiftDown(0);
}
// 判断当前优先级队列是否为空
public boolean isEmpty() {
return usedSize == 0;
}
/**
* 获取堆顶元素
* @return
*/
public int peekHeap() {
if (isEmpty()) {
System.out.println("当前优先级队列为空!");
return -1;
}
return elem[0];
}
}