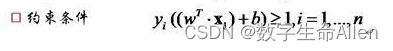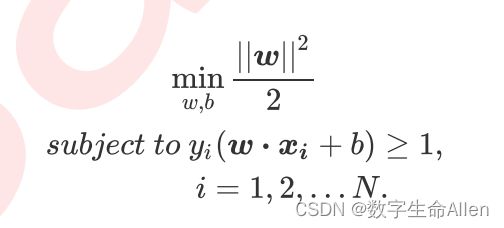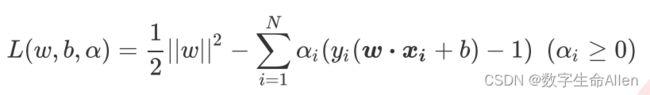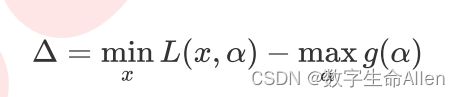线性【SVM】数学原理和算法实现
一. 数学原理
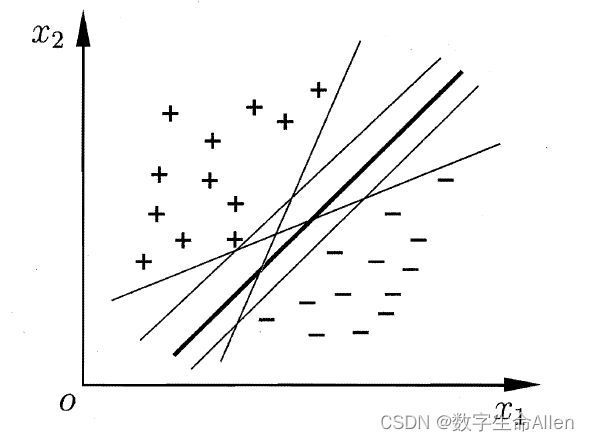
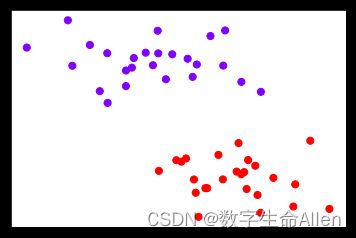
SVM是一类有监督的分类算法,它的大致思想是:假设样本空间上有两类点,如下图所示,我们希望找到一个划分超平面,将这两类样本分开,我们希望这个间隔能够最大化来使得模型泛化能力最强。
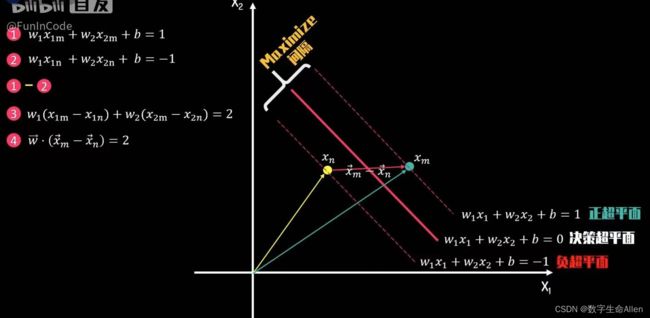
如上图所示,正超平面,负超平面和决策超平面的表达式如图所示,假设现在在正负超平面上有Xm和Xn两个支持向量,表达式分别是①,②,①减②得到③,③可以写成④的形式(其中,w向量 = (w1,w2),Xm向量 = (X1m,X2m),Xn向量 = (X1n,X2n))。
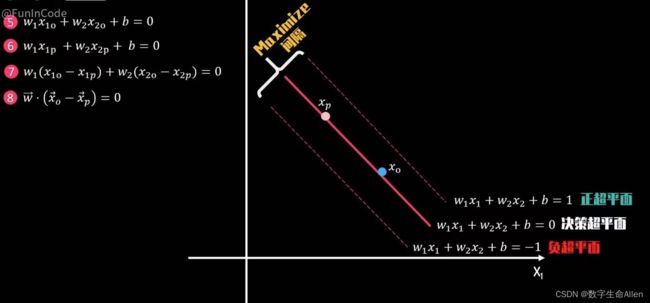
选择假设决策超平面上有Xp = (X1p,X2p)和Xo(X1o,X2o)两个向量,那么可以得到⑤和⑥,⑤-⑥ = ⑦,⑦可以写成⑧的形式。因此w向量是一个垂直于决策超平面的向量,即决策超平面的法向量。
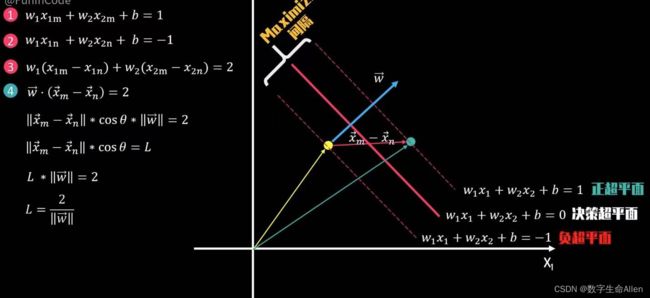
现在我们再回到④式,可以知道正负超平面之间的距离d可以表示为:d = 2/w的范数。
现在我们再来看约束条件,所有正超平面上方的点yi = 1,所有负超平面下方的点yi = -1,因此约束表达式可以写成:
所以这个优化问题就转变为一个典型的凸优化问题:
首先我们使用拉格朗日乘数来将损失函数改写成考虑了约束条件的形式:
上述式子被称为拉格朗日函数,其中αi就叫做拉格朗日乘数。此时此刻,我们要求解的就不只有参数向量和截距,我们也要求解拉格朗日乘数 ,而我们的Xi和Yi都是我们已知的特征矩阵和标签。对上面的式子分别对w和b求偏导,可以得到下述的结论:
在这里我们引入拉格朗日对偶函数。对于任何一个拉格朗日函数 L(x,α),都存在一个与它对应的对偶函数g(α) ,只带有拉格朗日乘数作为唯一的参数。如果L(x,α)的最优解存在并可以表示为 min L(x,α),并且对偶函数的最优解也存在 并可以表示为max g(α) ,则我们可以定义对偶差异,即拉格朗日函数的最优解与其对偶函数的最优解之间的差值:
如果 △ = 0,则称L(x,α)与其对偶函数之间存在强对偶关系,此时我们就可以通过求解其对偶函数的最优解来替代求解原始函数的最优解。在这里我们可以通过求对偶函数的最大值得到原函数的最小值。强对偶关系要想存在,必须满足KKT条件:
一旦KKT条件被满足,我们就可以通过求对偶函数的最大值来求出α的值。求出α后我们就可以通过结合上述的表达式求解出w和b,进而得到了决策边界的表达式。得到了决策边界的表达式就可以利用决策边界和其有关的超平面来分类了。
二. 算法实现
我们先来导入相应的模块:
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import matplotlib.pyplot as plt
import numpy as np使用make_blot函数绘制出散点图的坐标,并用plt.scatter绘制:
X,y = make_blobs(n_samples=50, centers=2, random_state=0,cluster_std=0.6)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")#rainbow彩虹色
plt.xticks([])
plt.yticks([])
plt.show()创建一个子图对象,以便后续操作:
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图为了绘制决策超平面,我们通过下面的代码块绘制网格点:
#获取平面上两条坐标轴的最大值和最小值
xlim = ax.get_xlim()
ylim = ax.get_ylim()
#在最大值和最小值之间形成30个规律的数据
axisx = np.linspace(xlim[0],xlim[1],30)
axisy = np.linspace(ylim[0],ylim[1],30)
axisy,axisx = np.meshgrid(axisy,axisx)
#我们将使用这里形成的二维数组作为我们contour函数中的X和Y
#使用meshgrid函数将两个一维向量转换为特征矩阵
#核心是将两个特征向量广播,以便获取y.shape * x.shape这么多个坐标点的横坐标和纵坐标
xy = np.vstack([axisx.ravel(), axisy.ravel()]).T
#其中ravel()是降维函数,vstack能够将多个结构一致的一维数组按行堆叠起来
#xy就是已经形成的网格,它是遍布在整个画布上的密集的点
plt.scatter(xy[:,0],xy[:,1],s=1,cmap="rainbow")
#理解函数meshgrid和vstack的作用
a = np.array([1,2,3])
b = np.array([7,8])
#两两组合,会得到多少个坐标?
#答案是6个,分别是 (1,7),(2,7),(3,7),(1,8),(2,8),(3,8)
v1,v2 = np.meshgrid(a,b)
v1
v2
v = np.vstack([v1.ravel(), v2.ravel()]).T接下来通过下面的代码块绘制出决策边界:
#建模,通过fit计算出对应的决策边界
clf = SVC(kernel = "linear").fit(X,y)#计算出对应的决策边界
Z = clf.decision_function(xy).reshape(axisx.shape)
#重要接口decision_function,返回每个输入的样本所对应的到决策边界的距离
#然后再将这个距离转换为axisx的结构,这是由于画图的函数contour要求Z的结构必须与X和Y保持一致
#首先要有散点图
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow")
ax = plt.gca() #获取当前的子图,如果不存在,则创建新的子图
#画决策边界和平行于决策边界的超平面
ax.contour(axisx,axisy,Z
,colors="k"
,levels=[-1,0,1] #画三条等高线,分别是Z为-1,Z为0和Z为1的三条线
,alpha=0.5#透明度
,linestyles=["--","-","--"])
ax.set_xlim(xlim)#设置x轴取值
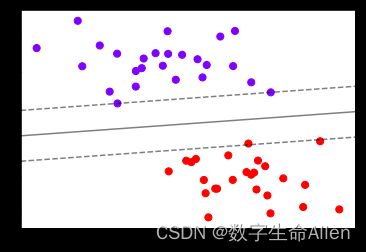
ax.set_ylim(ylim)可以看到决策边界和正负超平面已经被绘制出来了。
我们可以将上述过程打包成函数:
#将上述过程包装成函数:
def plot_svc_decision_function(model,ax=None):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
x = np.linspace(xlim[0],xlim[1],30)
y = np.linspace(ylim[0],ylim[1],30)
Y,X = np.meshgrid(y,x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)
ax.contour(X, Y, P,colors="k",levels=[-1,0,1],alpha=0.5,linestyles=["--","-","--"])
ax.set_xlim(xlim)
ax.set_ylim(ylim)
#则整个绘图过程可以写作:
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap="rainbow") # 画散点图
clf = SVC(kernel = "linear").fit(X,y) # 计算决策边界
plot_svc_decision_function(clf) # 画出决策边界下面是clf的一些属性:
clf.predict(X)
#根据决策边界,对X中的样本进行分类,返回的结构为n_samples
clf.score(X,y)
#返回给定测试数据和标签的平均准确度
clf.support_vectors_
#返回支持向量坐标
clf.n_support_#array([2, 1])
#返回每个类中支持向量的个数