【数据结构与算法】二叉树（基本操作和几种特殊二叉树介绍）

二叉树的基本介绍，只讲基本算法；对于特殊二叉树的相关算法，如AVL树的旋转，以后有时间再写。

一、基本概念

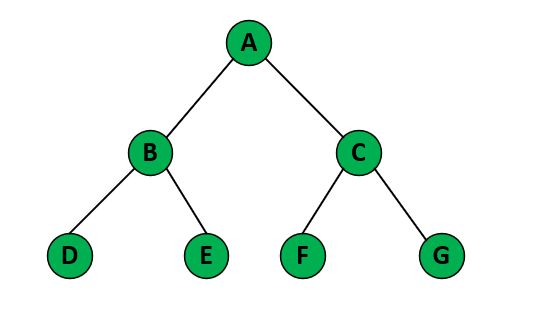
二叉树（Binary Tree）是一种树状数据结构，它由节点组成，每个节点最多有两个子节点：左子节点和右子节点。

这些节点通常包括一个根节点，从根节点开始，通过左子节点和右子节点的连接，形成一个树状结构。二叉树是计算机科学中的常见数据结构，用于解决许多问题，包括搜索、排序、图算法等。

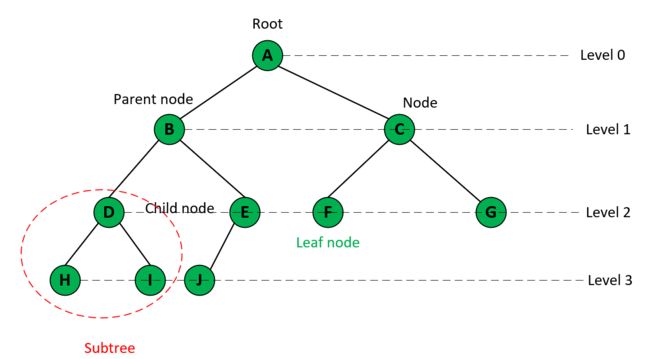
以下是二叉树的一些关键概念：

1. 根节点（Root）：树的顶端节点，是整个树的起始点。

2. 节点（Node）：树中的基本单元，每个节点包含一个值和两个指向子节点的指针（左子节点和右子节点）。

3. 父节点（Parent Node）：一个节点的直接上级节点。

4. 子节点（Child Node） ：一个节点的直接下级节点。

5. 叶子节点（Leaf Node）：没有子节点的节点，即左子节点和右子节点都为空的节点。

6. 子树（Subtree）：树中的任何节点和它的所有后代节点组成的树称为子树。

7. 深度（Depth）：节点到根节点的距离，根节点的深度为0。

8. 高度（Height）：树的最大深度，即从根节点到叶子节点的最长路径。

二、基本操作

2.1 二叉树的存储方式

二叉树可以以不同的方式进行存储和创建，其中两种常见的方式是使用链式存储和数组存储。

1. 链式存储：
   链式存储是一种常见的二叉树存储方式，其中每个节点由一个结构体或类表示，包含数据、左子节点指针和右子节点指针。节点之间通过指针来连接，构成树的结构

// 定义二叉树节点结构
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 创建一个新的二叉树节点
struct TreeNode* createTreeNode(int data) {
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    if (newNode == NULL) {
        printf("内存分配失败\n");
        exit(1);
    }
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

2. 数组存储：
   数组存储是另一种用于表示二叉树的方式，通常用于满二叉树和完全二叉树。在数组存储中，树的节点按照层序遍历的顺序存储在数组中，通过索引关系来表示节点之间的父子关系。一般来说，如果一个节点的索引为i，则其左子节点的索引为2i+1，右子节点的索引为2i+2，父节点的索引为(i-1)/2。

   创建一个数组表示的二叉树，需要按照层序遍历的顺序将节点数据存入数组中，并通过索引关系来表示树的结构。这种方式通常适用于满二叉树或完全二叉树，对于不规则的二叉树，可能会浪费一些空间。

2.2 常见操作

二叉树的基本操作包括以下几种：

1. 插入节点：将新的节点插入到二叉树中，通常按照一定的规则（如比较节点的值）确定新节点的位置。

2. 删除节点：从二叉树中删除指定节点，需要考虑不同情况下的情况，包括叶子节点、有一个子节点的节点和有两个子节点的节点。

3. 查找节点：在二叉树中查找特定值的节点，可以采用深度优先搜索（DFS）或广度优先搜索（BFS）等搜索算法。

4. 遍历二叉树：遍历二叉树是指按照一定顺序访问树中的所有节点，有以下几种遍历方式：

   • 先序遍历（Preorder Traversal）：根节点 -> 左子树 -> 右子树
   • 中序遍历（Inorder Traversal）：左子树 -> 根节点 -> 右子树
   • 后序遍历（Postorder Traversal）：左子树 -> 右子树 -> 根节点
   • 层序遍历（Level Order Traversal）：从上到下，从左到右逐层访问节点。

5. 查找最小值和最大值：在二叉搜索树（BST）中，可以轻松找到最小值和最大值，分别是最左边的节点和最右边的节点。

6. 求树的高度或深度：计算树的高度或深度是指从根节点到最深叶子节点的路径的长度。

7. 检查二叉树的平衡性：对于二叉搜索树，可以检查是否平衡以确保检索操作的效率。

8. 寻找最近公共祖先：在二叉树中，查找两个节点的最近公共祖先是一种常见操作，用于解决许多问题。

2.3 二叉树的遍历

2.31 前序遍历

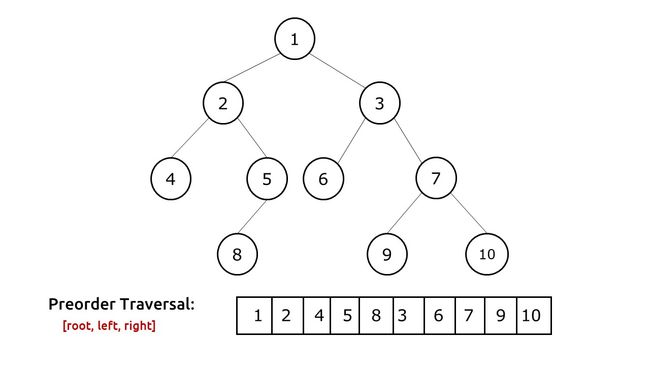
前序遍历（Preorder Traversal）是一种深度优先搜索（DFS）算法。

在前序遍历中，首先访问根节点，然后按照递归的方式依次访问左子树和右子树。这意味着在遍历的过程中，先访问父节点，然后依次访问其左子节点和右子节点。

前序遍历通常用于访问和处理树的所有节点，生成树的拷贝，或者生成树的字符串表示。以下是前序遍历的详细介绍和伪代码示例：

前序遍历的特点：

• 首先访问根节点。
• 随后递归地遍历左子树。
• 最后递归地遍历右子树。

前序遍历的伪代码：

PreorderTraversal(node):
    if node is not NULL:
        1. 处理当前节点（例如，打印节点的值）。
        2. 递归地调用PreorderTraversal(node->left)以遍历左子树。
        3. 递归地调用PreorderTraversal(node->right)以遍历右子树。

前序遍历的C语言简单示例：

#include 
#include 

// 定义二叉树节点结构
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 前序遍历函数
void preorderTraversal(struct TreeNode* node) {
    if (node != NULL) {
        // 1. 处理当前节点，例如，打印节点的值
        printf("%d ", node->data);
        // 2. 递归遍历左子树
        preorderTraversal(node->left);
        // 3. 递归遍历右子树
        preorderTraversal(node->right);
    }
}

int main() {
    // 创建一个二叉树
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->data = 1;
    root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->data = 2;
    root->left->left = NULL;
    root->left->right = NULL;
    root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->data = 3;
    root->right->left = NULL;
    root->right->right = NULL;

    // 执行前序遍历
    printf("前序遍历结果: ");
    preorderTraversal(root);
    printf("\n");

    // 释放二叉树内存
    free(root->left);
    free(root->right);
    free(root);

    return 0;
}

2.32 中序遍历

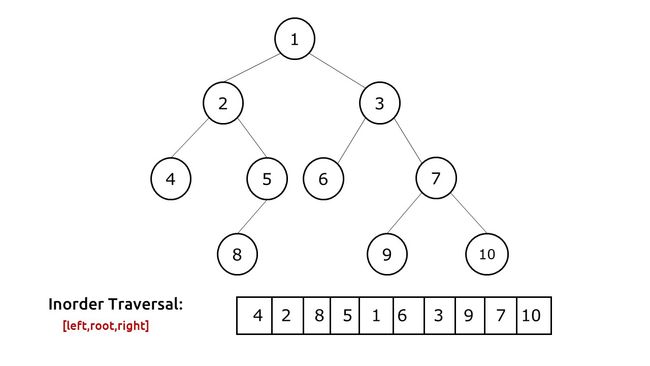
中序遍历（Inorder Traversal）是一种深度优先搜索（DFS）算法。在中序遍历中，首先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。这意味着在遍历的过程中，首先访问左子节点，然后访问父节点，最后访问右子节点。

中序遍历通常用于访问二叉搜索树（Binary Search Tree，BST）中的节点，以获得有序的数据。由于BST的特性，中序遍历可以让我们以升序方式访问树中的节点。

以下是中序遍历的详细介绍和伪代码示例：

中序遍历的特点：

• 首先递归地遍历左子树。
• 随后处理当前节点（例如，打印节点的值）。
• 最后递归地遍历右子树。

中序遍历的伪代码：

InorderTraversal(node):
    if node is not NULL:
        1. 递归地调用InorderTraversal(node->left)以遍历左子树。
        2. 处理当前节点（例如，打印节点的值）。
        3. 递归地调用InorderTraversal(node->right)以遍历右子树。

中序遍历的C语言简单示例：

#include 
#include 

// 定义二叉树节点结构
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 中序遍历函数
void inorderTraversal(struct TreeNode* node) {
    if (node != NULL) {
        // 1. 递归遍历左子树
        inorderTraversal(node->left);
        // 2. 处理当前节点，例如，打印节点的值
        printf("%d ", node->data);
        // 3. 递归遍历右子树
        inorderTraversal(node->right);
    }
}

int main() {
    // 创建一个二叉树
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->data = 2;
    root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->data = 1;
    root->left->left = NULL;
    root->left->right = NULL;
    root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->data = 3;
    root->right->left = NULL;
    root->right->right = NULL;

    // 执行中序遍历
    printf("中序遍历结果: ");
    inorderTraversal(root);
    printf("\n");

    // 释放二叉树内存
    free(root->left);
    free(root->right);
    free(root);

    return 0;
}

2.33 后序遍历

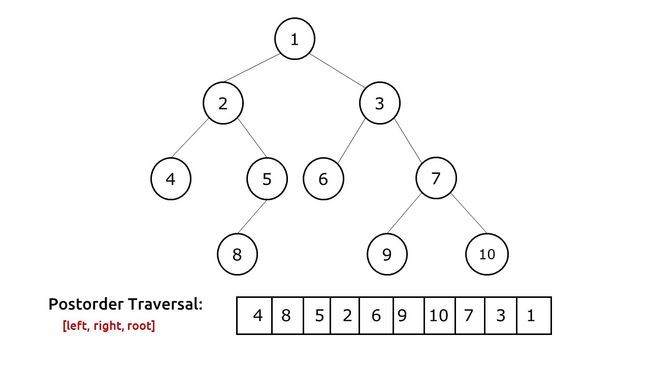
后序遍历（Postorder Traversal）是一种深度优先搜索（DFS）算法。在后序遍历中，**首先递归地遍历左子树，然后递归地遍历右子树，最后处理当前节点。**这意味着在遍历的过程中，首先访问左子节点，然后访问右子节点，最后访问父节点。

后序遍历通常用于释放树的内存，或在处理依赖于子节点的问题时使用，因为它确保子节点在父节点之前被处理。

以下是后序遍历的详细介绍和伪代码示例：

后序遍历的特点：

• 首先递归地遍历左子树。
• 随后递归地遍历右子树。
• 最后处理当前节点（例如，打印节点的值）。

后序遍历的伪代码：

PostorderTraversal(node):
    if node is not NULL:
        1. 递归地调用PostorderTraversal(node->left)以遍历左子树。
        2. 递归地调用PostorderTraversal(node->right)以遍历右子树。
        3. 处理当前节点（例如，打印节点的值）。

后序遍历的C语言简单示例：

#include 
#include 

// 定义二叉树节点结构
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 后序遍历函数
void postorderTraversal(struct TreeNode* node) {
    if (node != NULL) {
        // 1. 递归遍历左子树
        postorderTraversal(node->left);
        // 2. 递归遍历右子树
        postorderTraversal(node->right);
        // 3. 处理当前节点，例如，打印节点的值
        printf("%d ", node->data);
    }
}

int main() {
    // 创建一个二叉树
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->data = 2;
    root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->data = 1;
    root->left->left = NULL;
    root->left->right = NULL;
    root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->data = 3;
    root->right->left = NULL;
    root->right->right = NULL;

    // 执行后序遍历
    printf("后序遍历结果: ");
    postorderTraversal(root);
    printf("\n");

    // 释放二叉树内存
    free(root->left);
    free(root->right);
    free(root);

    return 0;
}

2.34 层序遍历

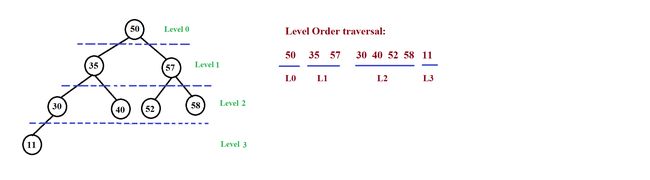
层序遍历（Level Order Traversal）是一种**广度优先搜索（BFS）**算法。在层序遍历中，首先访问根节点，然后按照树的层级顺序逐层访问节点。这意味着从根节点开始，依次访问每一层的节点，然后从左到右遍历下一层的节点，以此类推。

层序遍历通常使用队列数据结构来实现，因为它需要按照顺序访问每一层的节点。

以下是层序遍历的详细介绍和伪代码示例：

层序遍历的特点：

• 首先访问根节点。
• 逐层遍历每一层的节点，从左到右。
• 通常使用队列数据结构来实现。

层序遍历的伪代码：

LevelOrderTraversal(root):
    if root is NULL:
        return
    create an empty queue
    enqueue root into the queue
    while the queue is not empty:
        node = dequeue from the queue
        process(node)
        if node has a left child:
            enqueue left child into the queue
        if node has a right child:
            enqueue right child into the queue

层序遍历的C语言示例代码：

#include 
#include 

// 定义二叉树节点结构
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 层序遍历函数
void levelOrderTraversal(struct TreeNode* root) {
    if (root == NULL) {
        return;
    }

    // 创建一个队列用于层序遍历
    struct TreeNode* queue[100]; // 假设最多有100个节点
    int front = 0; // 队列前部
    int rear = 0; // 队列后部

    // 将根节点入队列
    queue[rear] = root;
    rear++;

    while (front < rear) {
        struct TreeNode* current = queue[front];
        front++;

        // 处理当前节点
        printf("%d ", current->data);

        // 将左子节点入队列
        if (current->left != NULL) {
            queue[rear] = current->left;
            rear++;
        }

        // 将右子节点入队列
        if (current->right != NULL) {
            queue[rear] = current->right;
            rear++;
        }
    }
}

int main() {
    // 创建一个二叉树
    struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->data = 1;
    root->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->data = 2;
    root->left->left = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->left->data = 4;
    root->left->left->left = NULL;
    root->left->left->right = NULL;
    root->left->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->left->right->data = 5;
    root->left->right->left = NULL;
    root->left->right->right = NULL;
    root->right = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    root->right->data = 3;
    root->right->left = NULL;
    root->right->right = NULL;

    // 执行层序遍历
    printf("层序遍历结果: ");
    levelOrderTraversal(root);
    printf("\n");

    // 释放二叉树内存
    free(root->left->left);
    free(root->left->right);
    free(root->left);
    free(root->right);
    free(root);

    return 0;
}

2.35 比较

遍历方式	特点	应用	优势
前序遍历	首先访问根节点，然后依次访问左子树和右子树	深度优先搜索、创建树的拷贝、生成字符串表示	可用于提前处理根节点，适用于搜索、序列化等问题
中序遍历	首先递归遍历左子树，然后访问根节点，最后递归遍历右子树	访问二叉搜索树中的节点、获取有序数据	在BST中按升序顺序访问节点，用于排序、搜索等问题
后序遍历	首先递归遍历左子树，然后递归遍历右子树，最后处理当前节点	释放树的内存、处理依赖于子节点的问题、表达式树计算	在处理子节点之前处理父节点，适用于清理资源、处理依赖关系等问题
层序遍历	首先访问根节点，然后逐层访问节点，通常使用队列	按层级遍历树、查找最短路径、广度优先搜索、构建层级结构	确保每一层的节点按顺序被访问，适用于广度优先搜索和层级分析

2.4 多种操作代码示例

代码演示了如何创建二叉树、插入节点、查找节点、删除节点、中序遍历二叉树以及释放二叉树内存。

#include 
#include 

// 定义二叉树节点结构
struct TreeNode {
    int data;
    struct TreeNode* left;
    struct TreeNode* right;
};

// 创建一个新的二叉树节点
struct TreeNode* createTreeNode(int data) {
    struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    if (newNode == NULL) {
        printf("内存分配失败\n");
        exit(1);
    }
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

// 插入节点到二叉树
struct TreeNode* insert(struct TreeNode* root, int data) {
    if (root == NULL) {
        return createTreeNode(data);
    }

    if (data < root->data) {
        root->left = insert(root->left, data);
    } else if (data > root->data) {
        root->right = insert(root->right, data);
    }

    return root;
}

// 查找节点
struct TreeNode* search(struct TreeNode* root, int data) {
    if (root == NULL || root->data == data) {
        return root;
    }

    if (data < root->data) {
        return search(root->left, data);
    }

    return search(root->right, data);
}

// 删除节点
struct TreeNode* delete(struct TreeNode* root, int data) {
    if (root == NULL) {
        return root;
    }

    if (data < root->data) {
        root->left = delete(root->left, data);
    } else if (data > root->data) {
        root->right = delete(root->right, data);
    } else {
        if (root->left == NULL) {
            struct TreeNode* temp = root->right;
            free(root);
            return temp;
        } else if (root->right == NULL) {
            struct TreeNode* temp = root->left;
            free(root);
            return temp;
        }

        struct TreeNode* temp = findMin(root->right);
        root->data = temp->data;
        root->right = delete(root->right, temp->data);
    }

    return root;
}

// 查找最小节点
struct TreeNode* findMin(struct TreeNode* node) {
    while (node->left != NULL) {
        node = node->left;
    }
    return node;
}

// 中序遍历二叉树
void inorderTraversal(struct TreeNode* root) {
    if (root != NULL) {
        inorderTraversal(root->left);
        printf("%d ", root->data);
        inorderTraversal(root->right);
    }
}

// 释放二叉树的内存
void freeBinaryTree(struct TreeNode* root) {
    if (root != NULL) {
        freeBinaryTree(root->left);
        freeBinaryTree(root->right);
        free(root);
    }
}

int main() {
    struct TreeNode* root = NULL;

    // 插入节点
    root = insert(root, 5);
    root = insert(root, 3);
    root = insert(root, 8);
    root = insert(root, 2);
    root = insert(root, 4);

    // 中序遍历并打印二叉树
    printf("中序遍历结果: ");
    inorderTraversal(root);
    printf("\n");

    // 查找节点
    int searchData = 4;
    struct TreeNode* foundNode = search(root, searchData);
    if (foundNode != NULL) {
        printf("找到节点 %d\n", searchData);
    } else {
        printf("未找到节点 %d\n", searchData);
    }

    // 删除节点
    int deleteData = 3;
    root = delete(root, deleteData);

    // 中序遍历并打印更新后的二叉树
    printf("中序遍历结果 (删除节点 %d 后): ", deleteData);
    inorderTraversal(root);
    printf("\n");

    // 释放二叉树内存
    freeBinaryTree(root);

    return 0;
}

三、特殊二叉树

有许多特殊类型的二叉树，它们在不同的应用中具有特定的性质和用途。

3.1 二叉搜索树（Binary Search Tree，BST）

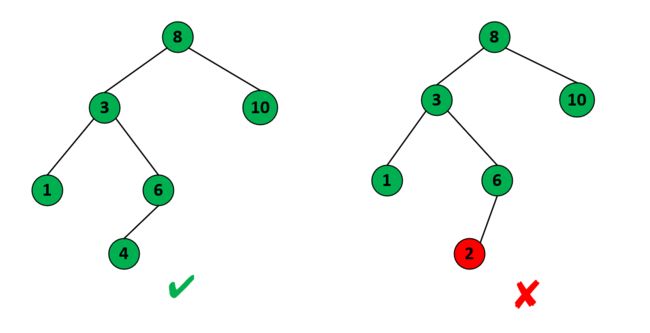
二叉搜索树（Binary Search Tree，BST）是一种特殊的二叉树，具有以下关键性质：

1. 有序性质：对于每个节点，其左子树中的所有节点的值都小于节点的值，而右子树中的所有节点的值都大于节点的值。这使得树具有有序性，使得在BST中进行查找、插入和删除操作非常高效。

2. 唯一性：BST中不允许重复的节点值。如果树中已经存在一个节点包含某个特定值，那么不允许再插入另一个具有相同值的节点。

二叉搜索树的有序性质使得它非常适合用于各种查找和排序操作。以下是一些关于二叉搜索树的重要特点和操作：

性质和特点：

• 对于任何节点，其左子树的值都小于该节点的值，右子树的值都大于该节点的值。

• 中序遍历BST会以升序的方式输出树中的节点值。

• BST的高度取决于插入和删除操作的顺序。在最坏情况下，BST可能会退化为链表，导致操作的时间复杂度变为O(n)。为了解决这个问题，通常使用平衡二叉树（如AVL树或红黑树）来维护树的平衡性。

基本操作：

1. 查找（Search）：查找树中是否存在特定值。从根节点开始，根据节点值的大小比较，可以递归或迭代地在树中查找目标值。

2. 插入（Insertion）：将新节点插入到BST中的适当位置，以保持树的有序性。插入操作从根节点开始，递归或迭代查找插入位置。

3. 删除（Deletion）：从BST中删除特定值的节点。删除操作可能需要处理不同的情况，如删除叶子节点、具有一个子节点的节点，以及具有两个子节点的节点。

复杂度：

• 平均情况下，查找、插入和删除操作的时间复杂度为O(log n)，其中n是树中节点的数量。这是因为在平衡的BST中，每次操作都会将搜索空间减半。

• 在最坏情况下，如果BST退化为链表，操作的时间复杂度可能为O(n)。

应用：

• 二叉搜索树广泛用于数据库系统中的索引结构，因为它可以高效地支持范围查询和快速查找。

• 用于排序算法的一种实现方式是通过构建BST并执行中序遍历来实现。

• BST也用于各种编程问题，如查找第K小的元素、寻找最近的公共祖先等。

BST的性能取决于插入和删除的顺序，如果插入或删除操作的顺序不当，可能导致树不平衡，从而影响性能。因此，为了维持BST的平衡性，通常使用自平衡二叉树（如AVL树和红黑树）来解决这个问题。

---

3.2 平衡二叉树（Balanced Binary Tree）

平衡二叉树（Balanced Binary Tree）是一种特殊的二叉搜索树，其设计目的是确保树的高度相对较小，以提高树上各种操作（查找、插入、删除等）的性能。在平衡二叉树中，树的左子树和右子树的高度之差通常被限制在一个常数范围内，通常是1。

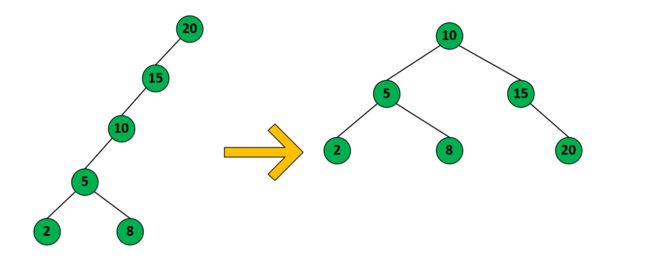
以下是平衡二叉树的主要特点和性质：

1. 平衡性：平衡二叉树的定义要求树的高度相对较小，以确保各种操作的平均时间复杂度保持在O(log n)的水平。

2. 二叉搜索树性质：平衡二叉树仍然是一棵二叉搜索树，具有BST的有序性质，即对于每个节点，左子树的值都小于节点的值，右子树的值都大于节点的值。

3. 平衡维护：为了保持平衡，平衡二叉树在插入和删除操作后会自动进行平衡维护。这通常涉及到旋转操作，以重新平衡树的结构。

4. 常见类型：AVL树和红黑树是两种常见的平衡二叉树。它们使用不同的平衡维护策略来确保树的平衡性。AVL树保持更严格的平衡，而红黑树牺牲了一些平衡性以获得更快的插入和删除性能。

3.21 AVL树

AVL树（Adelson-Velsky and Landis tree）是一种自平衡二叉搜索树，其设计目的是确保树的高度相对较小，以提高树上各种操作的性能。AVL树在1962年由两位前苏联的数学家 Adelson-Velsky 和 Landis 提出，是最早的自平衡二叉搜索树之一。

以下是AVL树的主要特点和性质：

1. 平衡性：AVL树要求树的任何节点的左子树和右子树的高度差（平衡因子）不超过1。这确保了树的高度相对较小，使得各种操作的平均时间复杂度为O(log n)，其中n是树中的节点数。

2. 二叉搜索树性质：AVL树仍然是一棵二叉搜索树，具有BST的有序性质，即对于每个节点，左子树的值都小于节点的值，右子树的值都大于节点的值。

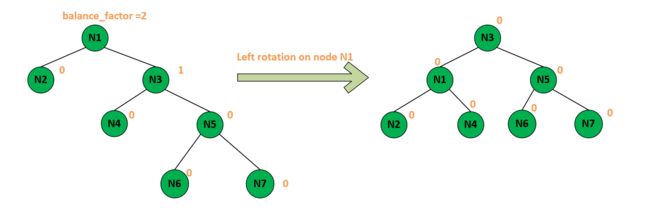
3. 平衡维护：为了保持平衡，AVL树在插入和删除操作后会自动进行平衡维护。如果插入或删除操作破坏了平衡性，AVL树会通过一系列旋转操作来恢复平衡。有四种基本类型的旋转：左旋（LL旋转）、右旋（RR旋转）、左-右旋（LR旋转）和右-左旋（RL旋转）。

4. 唯一性：AVL树中不允许重复的节点值。如果树中已经存在一个节点包含某个特定值，那么不允许再插入另一个具有相同值的节点。

5. 高度平衡性：AVL树的高度保持在一个较小的范围内，通常在O(log n)水平，这使得查询、插入和删除操作非常高效。

6. 复杂度：AVL树的查询操作的平均和最坏情况时间复杂度均为O(log n)，插入和删除操作的平均和最坏情况时间复杂度也为O(log n)。

AVL树是一种强平衡的二叉搜索树，但在维护平衡性方面较为严格，因此可能需要更多的旋转操作来保持平衡，这可能导致性能略低于其他自平衡树结构。尽管如此，AVL树仍然在许多应用中广泛使用，特别是在那些对性能有较高要求的场景中。

由于AVL树的平衡性要求比较高，插入和删除操作的开销较大，因此在某些情况下，红黑树等其他自平衡树结构可能更适合。选择树结构应基于特定应用的需求和性能要求。

3.22 红黑树

红黑树（Red-Black Tree）是一种自平衡二叉搜索树，它结合了二叉搜索树的有序性和平衡性。红黑树的设计目标是确保树的高度相对较小，从而保持各种操作的高效性能。红黑树在数据结构和算法中广泛应用，如C++ STL中的std::map和std::set，以及Java中的TreeMap和TreeSet。

以下是红黑树的主要特点和性质：

1. 平衡性：红黑树保持自平衡，确保树的高度相对较小。这使得树的各种操作的平均时间复杂度为O(log n)，其中n是树中的节点数。
2. 二叉搜索树性质：红黑树仍然是一棵二叉搜索树，具有BST的有序性质，即对于每个节点，左子树的值都小于节点的值，右子树的值都大于节点的值。
3. 节点颜色：每个节点都被标记为红色或黑色，这是红黑树的名字来源之一。这些颜色标记用于确保平衡性。
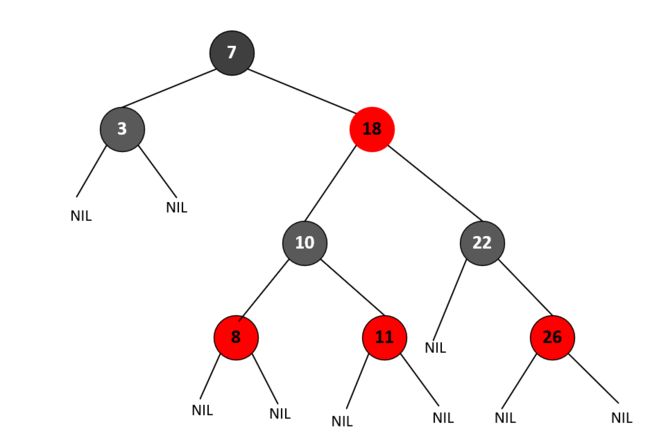
4. 根节点和叶子节点：根节点是黑色的，叶子节点通常是NIL节点，并被认为是黑色的。NIL节点是虚拟的节点，它们表示树的结束。
5. 红色节点规则：红色节点的父节点和子节点都不能是红色的。这个规则确保没有两个相邻的红色节点。
6. 黑高度规则：从任何一个节点到其每个叶子节点的路径上的黑色节点数量必须相等。这确保了树的平衡性。

基本操作：

红黑树的平衡是通过一系列插入和删除操作来维护的。以下是一些关于这些操作的基本概念：

• 插入操作：插入一个节点时，首先按照普通BST插入规则将节点插入到树中。然后，可能需要进行一系列颜色调整和旋转操作，以确保树保持红黑树的性质。

• 删除操作：删除一个节点时，首先按照BST删除规则删除节点。然后，可能需要进行一系列颜色调整和旋转操作，以确保树保持红黑树的性质。

复杂度：

• 查询、插入和删除操作的平均和最坏情况时间复杂度均为O(log n)，其中n是树中的节点数。

应用：

• 红黑树广泛用于各种编程问题和应用中，包括数据库系统的索引结构、高级编程语言的内置数据结构（如C++ STL和Java集合框架中的Map和Set）、文件系统、并发编程中的锁管理等领域。

• 红黑树的平衡性和高效性质使它成为一种非常重要的数据结构，对于需要高效地执行插入、删除和查找操作的应用非常有用。

---

3.3 满二叉树（Full Binary Tree）

满二叉树（Full Binary Tree），也称为真二叉树或严格二叉树，是一种特殊的二叉树结构。满二叉树具有以下关键特点和性质：

1. 节点数量：满二叉树的每一层都有最大可能数量的节点，即每层的节点数是前一层的两倍。这意味着满二叉树的节点数量为$2^{h+1}-1$，其中h是树的高度（有时候，也有人将根节点的深度定义为1，知道即可，就是1+2+4+8+…）。
2. 深度平衡：所有叶子节点都在树的最底层，使树保持平衡。因为每一层都有最大可能数量的节点，所以深度平衡性是满二叉树的一个显著特点。
3. 节点位置：满二叉树的节点按从左到右的顺序紧凑排列，没有空缺。这意味着满二叉树中的节点位置是有序的。

满二叉树是一种理想的二叉树结构，但在实际应用中，很少能够实现一个完全满足满二叉树条件的树，因为节点数通常不是2的幂。然而，满二叉树的概念在计算机科学中仍然非常有用，因为它帮助我们理解和分析二叉树算法的性能。

满二叉树的性质使其在某些情况下非常有用，包括以下方面：

1. 堆数据结构：满二叉树的特性使其成为堆数据结构的理想表示，如最大堆和最小堆，用于高效地实现优先队列等。
2. 完全二叉树和满二叉树的关系：完全二叉树是一种具有深度平衡特性的树结构，通常用于数组实现。满二叉树是完全二叉树的一个特例，其中所有层都被填充满。
3. 树的分析：满二叉树用于分析和理解二叉树操作的性能上界，如树的高度和节点数量。这有助于分析查找、插入、删除等操作的时间复杂度。

---

3.4 完全二叉树（Complete Binary Tree）

完全二叉树（Complete Binary Tree）是一种特殊类型的二叉树结构，具有一些重要的性质和特点。完全二叉树的定义要求树的节点按照从上到下、从左到右的顺序依次填充，没有空缺。以下是完全二叉树的主要特点和性质：

1. 节点填充：在完全二叉树中，从根节点开始，每一层都必须尽可能地填充节点，直到达到该层的最大可能节点数。只有最后一层可能不是满的，但如果有空缺，空缺节点必须位于该层的最右边。
2. 节点数量：如果完全二叉树的高度为h(假设跟节点度为0)，那么树中的节点数量通常接近于$2^{h+1}$ 。具体地，完全二叉树的节点数量可以表示为$2^h$到$2^{h+1}-1$之间。
3. 深度平衡：由于节点按层次填充，完全二叉树具有深度平衡性。这意味着树的高度相对较小，从根节点到叶子节点的深度之间的差异不会太大。
4. 数组表示：由于节点的排列方式，完全二叉树可以有效地表示为一个数组。可以使用数组索引来表示节点的位置，如父节点的索引为i，左子节点的索引为2i，右子节点的索引为2i+1(根节点除外，或者根节点索引为1,这些表示方法自己注意一下即可)。、

完全二叉树的性质使得它在实际应用中非常有用，特别是在数组实现二叉堆和堆排序等算法中。 以下是一些关于完全二叉树的应用和重要性：

• 堆数据结构：完全二叉树通常用于表示堆数据结构，如最小堆和最大堆。堆在优先队列、堆排序、图算法等方面具有广泛的应用。
• 数组实现：由于完全二叉树的结构，可以有效地将其表示为一个数组，这在内存中的连续存储非常有用。
• 二叉树的分析：完全二叉树用于分析和理解二叉树操作的性能上界，如树的高度和节点数量。这有助于分析查找、插入、删除等操作的时间复杂度。

---

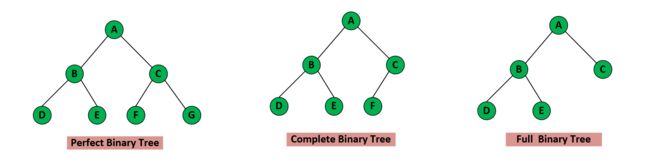
注意：国外的定义会有不同，分为完美二叉树、满二叉树和完全二叉树。

1. 完美二叉树（Perfect Binary Tree）：完美二叉树通常被定义为一种特殊的二叉树，其中每一层都被完全填充，没有空缺节点。它与满二叉树的定义相同，其中每一层的节点数是前一层的两倍。这个术语在国际上通常与满二叉树等效使用。

2. 满二叉树（Full Binary Tree）：满二叉树的定义是每个节点都具有零个或两个子节点，没有一个节点有一个子节点。这是国际通用的定义。

3. 完全二叉树（Complete Binary Tree）：完全二叉树的定义是一种特殊的二叉树，其中除了最后一层，其他所有层都被完全填充，且最后一层的节点都尽可能地从左到右填充。这个概念在国际上也是通用的，与国内的定义相同。

使用的时候注意上下文即可，不管怎么定义，最终都是要解决实际问题的。

3.5 二叉堆（Binary Heap）

二叉堆（Binary Heap）是一种特殊的二叉树结构，通常用于实现优先队列和堆排序等算法。二叉堆有以下特点和性质：

1. 二叉树结构：二叉堆是一种完全二叉树，通常用数组来实现。这种数组表示方式使得二叉堆的操作非常高效。

2. 堆属性：二叉堆有一个特殊的堆属性，通常分为两种类型：最小堆和最大堆。

   • 最小堆：在最小堆中，每个节点的值小于或等于其子节点的值，即根节点是树中的最小值。
   • 最大堆：在最大堆中，每个节点的值大于或等于其子节点的值，即根节点是树中的最大值。
     

3. 堆的操作：二叉堆支持以下基本操作：

   • 插入（Insertion）：将新元素插入堆中，并保持堆属性。
   • 删除最小（最大）元素（Extract-Min or Extract-Max）：从堆中删除并返回根节点的元素，然后重新组织堆以保持堆属性。
   • 查找最小（最大）元素（Find-Min or Find-Max）：获取根节点的元素值。
   • 堆排序：通过反复提取最小（最大）元素来对一组元素进行排序。
   • 减小（增加）元素的值：将元素的值减小（增加），然后重新组织堆以保持堆属性。

4. 时间复杂度：二叉堆的基本操作（插入、删除、查找最小或最大）的时间复杂度为O(log n)，其中n是堆中元素的数量。这使得二叉堆在实现优先队列等需要高效插入和删除操作的场景中非常有用。

5. 堆的实现：二叉堆通常通过数组实现，其中根节点存储在数组的第一个位置（索引为0或1），而每个节点的左子节点和右子节点分别存储在数组中的不同位置。这种表示方式使得堆的操作非常高效，不需要指针和额外的空间。

6. 堆的应用：二叉堆在各种应用中非常有用，包括：

   • 实现优先队列，用于高效处理具有不同优先级的任务。
   • 图算法中的最短路径算法（例如Dijkstra算法）。
   • 堆排序算法，用于对一组元素进行排序。
   • 以及其他需要高效查找最小或最大元素的场景。

此外，堆也可以是内存中的一块区域，堆内存是一种用于动态分配和释放内存的数据结构，通常用于存储运行时数据。

3.6 线索二叉树（Threaded Binary Tree）

线索二叉树（Threaded Binary Tree）是一种对普通二叉树的改进，旨在加快对树的遍历操作，特别是中序遍历。

线索二叉树的主要思想是在二叉树节点中添加线索（指针），以使遍历过程更加高效。线索二叉树有两种常见的类型：前序线索二叉树和中序线索二叉树。

3.61 中序线索二叉树

中序线索二叉树是最常见的线索二叉树类型，它在二叉树的节点中添加线索以支持中序遍历。在中序线索二叉树中，每个节点有以下线索指针：

• left_thread：指向节点的左子节点（如果存在）或中序遍历前驱节点。
• right_thread：指向节点的右子节点（如果存在）或中序遍历后继节点。

中序线索二叉树的特点：

• 所有叶子节点的left_thread和right_thread都指向其前驱节点和后继节点，以形成一个循环链表。
• 中序遍历中，遍历过程可以在不需要递归或栈的情况下直接通过线索指针进行。

3.62 前序线索二叉树

前序线索二叉树是一种改进，旨在支持前序遍历。在前序线索二叉树中，每个节点有以下线索指针：

• left_thread：指向节点的左子节点（如果存在）或前序遍历前驱节点。
• right_thread：指向节点的右子节点（如果存在）或前序遍历后继节点。

前序线索二叉树的特点：

• 所有叶子节点的left_thread和right_thread都指向其前驱节点和后继节点，以形成一个循环链表。
• 前序遍历中，遍历过程可以在不需要递归或栈的情况下直接通过线索指针进行。

3.63 遍历线索二叉树

遍历线索二叉树时，可以使用线索指针在树中移动，无需使用递归或栈。以下是遍历线索二叉树的一般步骤：

• 中序遍历线索二叉树：

  1. 从根节点出发，一直跟随left_thread指针，直到到达最左的叶子节点。
  2. 处理当前节点。
  3. 如果有right_thread指针，直接跳到下一个节点；否则，转向右子节点并重复步骤1。

• 前序遍历线索二叉树：

  1. 从根节点出发，处理当前节点。
  2. 如果有left_thread指针，直接跳到下一个节点；否则，转向左子节点并重复步骤1。
  3. 如果有right_thread指针，直接跳到下一个节点；否则，转向右子节点并重复步骤1。

线索二叉树的主要优势是在不需要递归或栈的情况下实现遍历，从而节省内存和提高遍历效率。然而，线索化操作会增加树的维护复杂性，因此通常仅在对树进行频繁遍历而很少更改结构时才使用。

3.7 哈夫曼树（Huffman Tree）

哈夫曼树（Huffman Tree）是一种用于数据压缩的树状数据结构，特别适用于构建变长编码的算法，其中字符出现频率高的字符被分配较短的编码，而频率低的字符被分配较长的编码。哈夫曼树是一种最优二叉树，以使整体编码长度最短，从而实现高效的数据压缩。

1. 哈夫曼编码

   • 哈夫曼编码：哈夫曼编码是一种可变长度编码方式，其中出现频率高的字符被分配较短的编码，而出现频率低的字符被分配较长的编码。这样可以减少整体编码长度，从而实现数据压缩。哈夫曼编码是一种无损压缩方法，意味着原始数据可以完全还原，不会丢失信息。

   • 编码表：为了生成哈夫曼编码，需要构建一个字符到编码的映射表，通常以树的形式来表示，这就是哈夫曼树。

2. 哈夫曼树的构建

   1. 初始化：将每个字符作为一个单独的树（称为"叶子树"）。

   2. 频率计算：计算每个字符在原始数据中出现的频率。

   3. 合并：重复以下步骤直到只剩下一个树：

      • 从已有的树中选择两个具有最低频率的树。
      • 将它们合并为一个新的树，其中根节点的频率等于两个子树的频率之和。

   4. 树构建完成：此时，得到的单一树就是哈夫曼树。

3. 哈夫曼树的特点

   • 哈夫曼树是一棵二叉树，每个非叶子节点都有两个子节点。

   • 哈夫曼树的叶子节点对应于输入中的字符，并且包含它们的频率信息。

   • 哈夫曼树的根节点包含了整个编码的结构，是树的根路径。

4. 生成编码

   • 在哈夫曼树中，从根节点到每个叶子节点的路径上的左分支用0表示，右分支用1表示。这样可以生成每个字符的哈夫曼编码。

   • 哈夫曼编码的长度取决于字符在树中的深度，因此频率高的字符拥有较短的编码。

5. 应用

   • 哈夫曼树和哈夫曼编码在数据压缩领域广泛应用，如在文件压缩、图像压缩、音频压缩和通信领域中。它们还在各种编码和加密算法中发挥作用。

例子：https://www.geeksforgeeks.org/huffman-coding-greedy-algo-3/

3.8 三叉树（Ternary Tree）

三叉树是一种具有三个子节点的树结构。它不像二叉树那样常见，但在某些应用中可能有用。

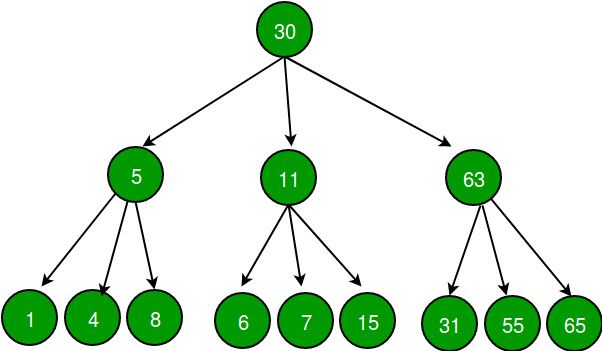
三叉树在某些特定应用中非常有用，尤其是在自然语言处理（NLP）和语法分析中。它可以用于构建分析树（Parse Tree），这是在语法分析中用于表示语法结构的树形结构。

在分析树中，节点代表语法构造，子节点表示构造的组成部分。三叉树可以更好地表示一些语法结构，如上下文无关文法（Context-Free Grammar）中的某些规则，因此在自然语言处理中，三叉树用于构建语法分析树以解析句子的结构。

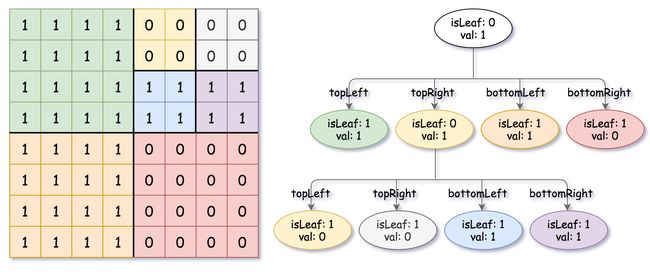
3.9 四叉树（Quadtree）

四叉树（Quadtree）是一种树状数据结构，用于分割二维空间，特别适用于在计算机图形、地理信息系统（GIS）、计算机游戏等领域中进行空间数据管理和查询。四叉树之所以得名是因为每个节点最多可以分裂成四个子节点。

1. 结构和性质

   四叉树的基本思想是将一个矩形区域分割成四个相等的子矩形，以创建树节点。每个节点可以有以下几种情况：

   • 空节点：表示没有数据，是叶子节点。
   • 叶子节点：包含一个数据项，通常是一个点或一个区域。
   • 内部节点：没有数据项，但有四个子节点，每个子节点代表一个子区域。

   四叉树的关键性质：

   • 递归性：四叉树是递归的数据结构，树中的每个内部节点都包含四个子节点，每个子节点也可以是一个四叉树。

   • 空间分割：四叉树有效地将空间分割成四个子区域，每个子区域可以进一步分割。

   • 灵活性：四叉树可以根据需要动态扩展或压缩，以适应不同的数据分布。

2. 应用领域

   四叉树在许多领域中有广泛的应用，包括但不限于：

   • 计算机图形：用于加速碰撞检测、空间分区和渲染等图形处理任务。

   • 地理信息系统（GIS）：用于管理和查询地理数据，如地图、地形和遥感图像。

   • 计算机游戏：用于进行场景管理、视锥剔除和碰撞检测。

   • 图像处理：用于图像分割、特征检测和空间索引。

   • 自然语言处理：用于解析句子结构，如句法树。

四叉树是一种强大的空间数据结构，可以加速空间查询和管理。它的应用范围广泛，适用于需要处理大规模空间数据的许多领域。

3.10 KD树（K-Dimensional Tree）

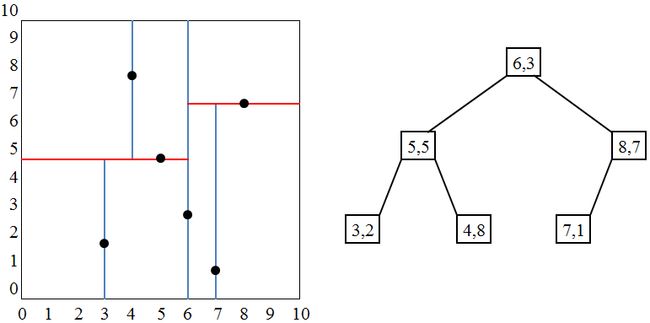
KD树（K-Dimensional Tree）是一种用于高维空间的数据结构，通常用于空间划分和高维点查询。KD树的主要思想是将多维空间递归地分割成二维空间，并在每个节点中存储一个点，以支持高效的点查询和范围搜索。

1. 结构和性质

   KD树是一棵二叉树，其中每个节点代表一个k维点，通常是一个具有k个坐标值的点。每个节点分割k维空间的一个超平面，将空间分成两个半区域，一个包含所有点的左子区域，另一个包含所有点的右子区域。

   • 选择切分维度：在每个节点上，需要选择一个维度（坐标轴）作为切分维度。通常，选择维度是根据轮流选取或根据最大方差的维度选取。

   • 切分值：选取维度后，根据该维度上点的中值来选择切分值，将小于切分值的点放在左子区域，大于等于切分值的点放在右子区域。

   • 平衡性：与二叉搜索树不同，KD树并不一定是平衡的，但在实际应用中，通常保持接近平衡，以保证查询效率。

2. 应用领域

   KD树在各种领域中有广泛的应用，包括但不限于：

   • 机器学习和数据挖掘：用于最近邻搜索、聚类和分类。
   • 计算机图形学：用于空间分区、碰撞检测和渲染。
   • 生物信息学：用于基因序列比对和医学图像处理。
   • 数据库查询优化：用于高维数据索引。
   • 自然语言处理：用于文本分类和信息检索。