数据结构与算法——二叉树的实现与原理
目录
一、二叉树的原理
1.二叉树的基本概念
2.树的性质
3.二叉树的性质
二、二叉树的实现
1.二叉树的定义
2.二叉树的创建
3.前序遍历
4.中序遍历
5.后序遍历
6.层序遍历
7.二叉树的节点的个数
8.二叉树的叶子节点的个数
9.二叉树第k层节点个数
10.二叉树查找值为x的节点
11.判断二叉树是否是完全二叉树
12.二叉树销毁
一、二叉树的原理
1.二叉树的基本概念
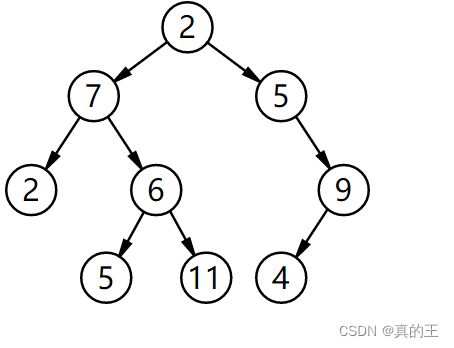
在电脑科学中,二叉树(英语:Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。
与普通树不同,普通树的节点个数至少为1,而二叉树的节点个数可以为0;普通树节点的最大分支度没有限制,而二叉树节点的最大分支度为2;普通树的节点无左、右次序之分,而二叉树的节点有左、右次序之分。
二叉树通常作为数据结构应用,典型用法是对节点定义一个标记函数,将一些值与每个节点相关系。这样标记的二叉树就可以实现二叉搜索树和二叉堆,并应用于高效率的搜索和排序。
一个节点也可以称为树
一个空指针也可被称为树——空树
除根节点其它节点互不相交
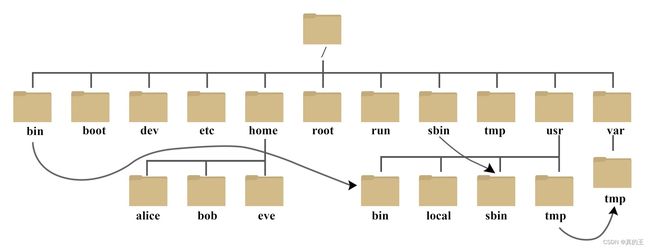
我们电脑的文件就是树型结构
2.树的性质
节点的度:一个节点含有的子树的个数称为该节点的度
叶节点或终端节点:度为0的节点称为叶节点
3.二叉树的性质
二、二叉树的实现
1.二叉树的定义
我们用链表递归定义二叉树
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType _data;
struct BinaryTreeNode* _left;
struct BinaryTreeNode* _right;
}BTNode;2.二叉树的创建
通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
又因为我们是递归定义,记录数组下标的i需要传递它的指针
通过前序遍历来实现
BTNode* BuyBTNode(BTDataType x)
{
BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));
newNode->_data = x;
newNode->_left = NULL;
newNode->_right = NULL;
return newNode;
}
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
BTNode* root = BuyBTNode(a[(*pi)++]);
root->_left = BinaryTreeCreate(a, n, pi);
root->_right = BinaryTreeCreate(a, n, pi);
return root;
}3.前序遍历
这几种遍历方式,所说的序是指访问根的顺序,前序遍历是指先访问根,然后左子树,右子树
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("# ");
return;
}
printf("%c ", root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}4.中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
{
printf("# ");
return;
}
BinaryTreePrevOrder(root->_left);
printf("%c ", root->_data);
BinaryTreePrevOrder(root->_right);
}5.后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
{
printf("# ");
return;
}
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
printf("%c ", root->_data);
}
6.层序遍历
层序遍历与前三种遍历方式稍有不同,层序遍历是指一层一层的遍历,从上到下
我们就要借助队列来实现,我们每次先让二叉树中的节点入队列,获取队列头部的节点,
头部节点又带着它的左右子树,让它的左右子树入队列,一直循环下去,直到队列为空,就算遍历完成了
void BinaryTreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root != NULL)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->_data);
if (front->_left != NULL)
{
QueuePush(&q, front->_left);
}
if (front->_right != NULL)
{
QueuePush(&q, front->_right);
}
}
printf("\n");
QueueDestroy(&q);
}7.二叉树的节点的个数
二叉树节点的个数,我们按照分治的思想,一颗树节点的个数等于它的左子树的节点的个数加上它的右子树节点的个数在加上它自己就是整棵树的节点数量
int BinaryTreeSize(BTNode* root)
{
return root == NULL ? 0 : BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}8.二叉树的叶子节点的个数
叶子节点个数的求法与整棵树的节点求法类似,叶子就是它的左右子树均为空,那么递归到它的左右子树都是NULL就返回1,它自身为空就返回0,然后整棵树的叶子结点就等于左子树的叶子加上右子树叶子节点的数量
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->_left == NULL && root->_right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}9.二叉树第k层节点个数
求树的第k层节点的个数就可以转化成1求左子树第k-1层的节点个数加上右子树第k-1层节点的个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1) + 1;
}10.二叉树查找值为x的节点
查找就算是比较简单了,我们要先在左树中查找,查看是否有那个元素,如果左树没有,再去右树中查找,左右树均没有,就代表没有找到
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->_data == x)
{
return root;
}
BTNode* ret1 = BinaryTreeFind(root->_left, x);
if (ret1)
{
return ret1;
}
BTNode* ret2 = BinaryTreeFind(root->_right, x);
if (ret2)
{
return ret2;
}
return NULL;
}
11.判断二叉树是否是完全二叉树
判断是否是完全二叉树,我们也需要使用队列,我们将二叉树的全部节点都存到队列中,然后判断队列中的NULL是否是连续的来判断是否是完全二叉树
如果NULL不是连续的那么说明就不是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BTNode* tmp = QueueFront(&q);
QueuePop(&q);
if (tmp != NULL)
{
QueuePush(&q, tmp->_left);
QueuePush(&q, tmp->_right);
}
else
{
break;
}
}
while (!QueueEmpty(&q))
{
BTNode* tmp = QueueFront(&q);
QueuePop(&q);
if (tmp != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}12.二叉树销毁
销毁我们只要后序遍历就好了
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestory(root->_left);
BinaryTreeDestory(root->_right);
free(root);
}