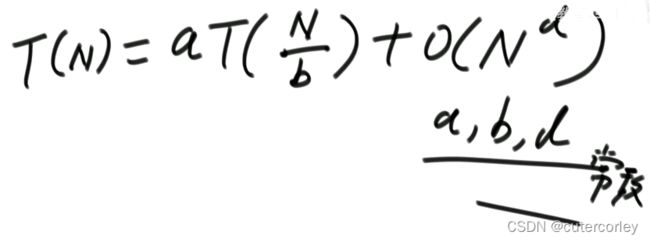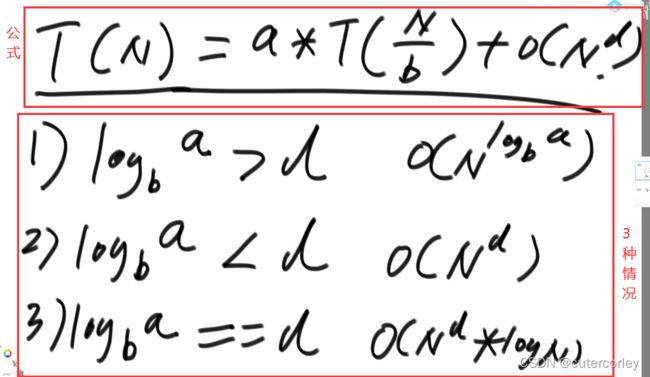算法与数据结构全阶班-左程云版(二)基础阶段之2.链表、栈、队列、递归行为、哈希表和有序表
文章目录
- 引言
- 1.链表结构
- 2.栈和队列
- 3.递归
- 4.哈希表和有序表
- 总结
引言
本文主要介绍了一些常用的数据结构,包括链表、栈、队列、递归、哈希表和有序表。
1.链表结构
单链表节点结构:
class Node {
public int value;
public Node next;
public Node(int data) {
value = data;
}
}
双向链表节点结构:
class DoubleNode {
public int value;
public DoubleNode last;
public DoubleNode next;
public DoubleNode(int data) {
value = data;
}
}
简单练习:
1)单链表和双链表如何反转
2)把给定值都删除
实现如下:
// 反转单链表
public static Node reverseLinkedList(Node head) {
Node pre = null;
Node next = null;
while (null != head) {
next = head.next;
head.next = pre;
pre = head;
head = next;
}
return pre;
}
// 反转双向链表
public static DoubleNode reverseDoubleList(DoubleNode head) {
DoubleNode pre = null;
DoubleNode next = null;
while (null != head) {
next = head.next;
head.next = pre;
head.last = next;
pre = head;
head = next;
}
return pre;
}
// 删除单链表元素
public static Node removeValue(Node head, int num) {
// 跳过链表头部值为num的部分
while (head != null) {
if (head.value != num) {
break;
}
head = head.next;
}
// 头节点为第一个值不为num的节点
Node pre = head;
Node cur = head;
while (cur != null) {
// pre始终保持其值不等于num
if (num == cur.value) {
pre.next = cur.next;
} else {
pre = cur;
}
cur = cur.next;
}
return head;
}
// 删除双向链表元素
public static DoubleNode removeValue(DoubleNode head, int num) {
// 跳过头节点
while (head != null) {
if (head.value != num) {
break;
}
head = head.next;
}
if (head != null) {
head.last = null;
}
DoubleNode cur = head, pre = head;
while (cur != null) {
if (cur.value == num) {
pre.next = cur.next;
cur.last = null;
} else {
pre = cur;
}
cur = cur.next;
}
return head;
}
Java和C++在垃圾回收方面存在区别:
当一块内存空间所对应的变量或引用不存在时,就会自动释放这块内存,Java存在内存泄漏的原因是因为变量的生命周期不同,例如一个生命周期较短的方法中对一个生命周期更长的数据结构进行了操作,但是调用结束时并没有恢复,简单来说,内存空间找不到对应变量或引用就会被释放,否则就不会被释放;
C++ 内存泄漏是因为声明的变量忘记释放,必须手动调用函数释放。
2.栈和队列
栈:数据先进后出,犹如弹匣;
队列:数据先进先出,好似排队。
栈和队列的实现:
(1)基于双向链表
package structure02;
/**
* @author Corley
* @date 2021/10/7 14:02
* @description LeetCodeAlgorithmZuo-structure02
*/
public class LinkedListQueueStack {
/*
自定义节点
*/
static class Node<T> {
public Node<T> last;
public Node<T> next;
public T value;
public Node(T value) {
this.value = value;
}
}
/*
自定义双向链表
*/
static class DoubleLinkedList<T> {
public Node<T> head;
public Node<T> tail;
public void addFromHead(T value) {
Node<T> cur = new Node<>(value);
if (null == head) {
head = cur;
tail = cur;
} else {
cur.next = head;
head.last = cur;
head = cur;
}
}
public void addFrombottom(T value) {
Node<T> cur = new Node<>(value);
if (null == head) {
head = cur;
tail = null;
} else {
cur.last = tail;
tail.next = cur;
tail = cur;
}
}
public T popFromHead() {
if (null == head) {
return null;
}
T res = head.value;
if (head == tail) {
head = null;
tail = null;
} else {
head = head.next;
head.last = null;
}
return res;
}
public T popFromBottom() {
if (null == head) {
return null;
}
T res = tail.value;
if (head == tail) {
head = null;
tail = null;
} else {
tail = tail.last;
tail.next = null;
}
return res;
}
public boolean isEmpty() {
return null == head;
}
}
/*
自定义栈
*/
static class Stack<T> {
private final DoubleLinkedList<T> stack;
public Stack() {
stack = new DoubleLinkedList<>();
}
public void push(T value) {
stack.addFromHead(value);
}
public T pop() {
return stack.popFromHead();
}
public boolean isEmpty() {
return stack.isEmpty();
}
}
/*
自定义队列
*/
static class Queue<T> {
private final DoubleLinkedList<T> queue;
public Queue() {
queue = new DoubleLinkedList<>();
}
public void push(T value) {
queue.addFromHead(value);
}
public T pop() {
return queue.popFromBottom();
}
public boolean isEmpty() {
return queue.isEmpty();
}
}
}
(2)基于数组
使用数组时,需要考虑数组的大小问题,这里选择使用固定长度的数组来实现。
其中,数组实现较麻烦,如下:
数组实现队列时,使用环形数组的思想实现,即RingBuffer的原理,具体可参考https://blog.csdn.net/jkqwd1222/article/details/82194305。
实现如下:
package structure02;
/**
* @author Corley
* @date 2021/10/7 14:50
* @description LeetCodeAlgorithmZuo-structure02
* 使用环形数组RingBuffer的思想实现队列
*/
public class ArrayQueueStack {
static class Queue {
private final int[] arr;
private int pushi; // 加元素的下标
private int pulli; // 取元素的下标
private int size;
private final int limit; // 队列大小
public Queue(int limit) {
arr = new int[limit];
pushi = 0;
pulli = 0;
size = 0;
this.limit = limit;
}
public void push(int num) {
if (size == limit) {
throw new RuntimeException("队列已满,不能再添加元素!");
}
size++;
arr[pushi] = num;
pushi = nextIndex(pushi);
}
public int pull() {
if (isEmpty()) {
throw new RuntimeException("队列已空,不能再取元素!");
}
size--;
int res = arr[pulli];
pulli = nextIndex(pulli);
return res;
}
public boolean isEmpty() {
return 0 == size;
}
private int nextIndex(int index) {
return index < (limit - 1) ? (index + 1) : 0;
}
}
class Stack {
int[] arr;
int size;
int limit;
public Stack(int limit) {
arr = new int[limit];
this.limit = limit;
size = 0;
}
public void push(int num) {
if (size == limit) {
throw new RuntimeException("栈已满,不能再添加元素!");
}
arr[size++] = num;
}
public int pop() {
if (0 == size) {
throw new RuntimeException("栈已空,不能再取元素!");
}
return arr[--size];
}
}
}
既然语言都提供了这些结构和API,为什么还需要手写代码:
1)算法问题无关语言;
2)语言提供的API是有限的,当有新的功能是API不提供的就需要改写;
3)任何软件工具的底层都是最基本的算法和数据结构,这是绕不过去的。
实现一个特殊的栈,在基本功能的基础上,再实现返回栈中最小元素的功能
1)pop: push、getMin操作的时间复杂度都是O(1);
2)设计的栈类型可以使用现成的栈结构。
实现思路1如下:
维护两个栈,一个栈保存数据,另一个栈保存到当前高度的最小值,如下:
实现如下:
static class MinStack1 {
private final Stack<Integer> stackData;
private final Stack<Integer> stackMin;
public MinStack1() {
this.stackData = new Stack<>();
this.stackMin = new Stack<>();
}
public void push(int num) {
if (this.stackMin.isEmpty()) {
this.stackMin.push(num);
} else if (num < this.stackMin.peek()) {
this.stackMin.push(num);
} else {
this.stackMin.push(this.stackMin.peek());
}
this.stackData.push(num);
}
public int pop() {
if (this.stackData.isEmpty()) {
throw new RuntimeException("Your stack is empty!");
}
stackMin.pop();
return stackData.pop();
}
public int getMin() {
if (this.stackData.isEmpty()) {
throw new RuntimeException("Your stack is empty!");
}
return stackMin.peek();
}
}
实现思路2如下:
维护两个栈,一个栈保存数据,一个栈保存到当前高度的最小值,但是只有当当前要入栈的数≤之前(栈下面)的最小值时才入最小栈,会节省一些空间,但是会增加时间,因为增加了逻辑判断,如下:
实现如下:
static class MinStack2 {
private final Stack<Integer> stackData;
private final Stack<Integer> stackMin;
public MinStack2() {
this.stackData = new Stack<>();
this.stackMin = new Stack<>();
}
public void push(int num) {
if (this.stackMin.isEmpty()) {
this.stackMin.push(num);
} else if (num <= this.stackMin.peek()) {
this.stackMin.push(num);
}
this.stackData.push(num);
}
public int pop() {
if (this.stackData.isEmpty()) {
throw new RuntimeException("Your stack is empty!");
}
int res = stackData.pop();
if (res == getMin()) {
stackMin.pop();
}
return res;
}
public int getMin() {
if (this.stackData.isEmpty()) {
throw new RuntimeException("Your stack is empty!");
}
return stackMin.peek();
}
}
栈和队列的常见面试题:
1)如何用栈结构实现队列结构;
2)如何用队列结构实现栈结构。
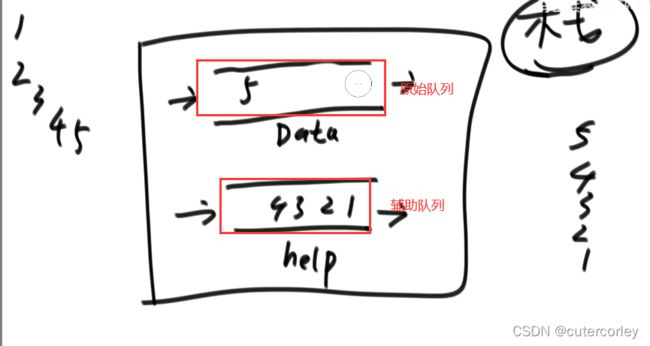
用队列实现栈:
用两个队列来实现,包括原始队列和辅助队列,如下:
两个队列角色互相切换。
实现如下:
static class TwoQueueStack<T> {
private Queue<T> queue;
private Queue<T> help;
public TwoQueueStack() {
queue = new LinkedList<>();
help = new LinkedList<>();
}
public void push(T value) {
queue.offer(value);
}
public T pop() {
while (queue.size() > 1) {
help.offer(queue.poll());
}
T res = queue.poll();
Queue<T> tmp = queue;
queue = help;
help = tmp;
return res;
}
public T peek() {
while (queue.size() > 1) {
help.offer(queue.poll());
}
T res = queue.poll();
help.offer(res);
Queue<T> tmp = queue;
queue = help;
help = tmp;
return res;
}
public boolean isEmpty() {
return queue.isEmpty();
}
}
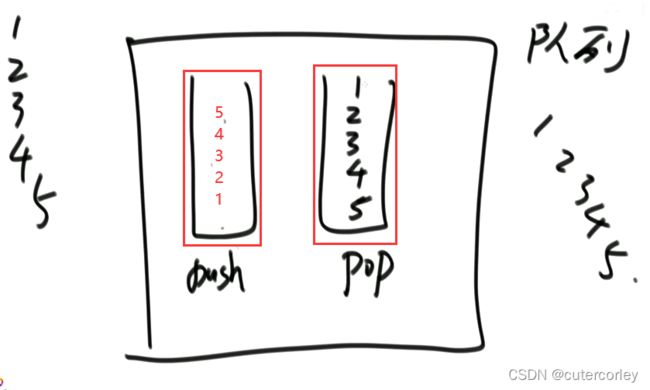
用栈实现队列:
也是用两个栈来实现,包括push栈和pop栈,如下:
遵循的原则:
pop栈为空时,才能将数据导入到pop栈中;
push栈导数据到pop栈时,一次导完。
实现如下:
static class TwoStackQueue {
private final Stack<Integer> stackPush;
private final Stack<Integer> stackPop;
public TwoStackQueue() {
stackPush = new Stack<>();
stackPop = new Stack<>();
}
// push栈向pop栈导入数据
private void pushToPop() {
if (stackPop.isEmpty()) {
while (!stackPush.isEmpty()) {
stackPop.push(stackPush.pop());
}
}
}
public void add(int num) {
stackPush.push(num);
pushToPop();
}
public int poll() {
if (stackPush.isEmpty() && stackPop.isEmpty()) {
throw new RuntimeException("Queue is empty!");
}
pushToPop();
return stackPop.pop();
}
public int peek() {
if (stackPush.isEmpty() && stackPop.isEmpty()) {
throw new RuntimeException("Queue is empty!");
}
pushToPop();
return stackPop.peek();
}
}
面试:
一般情况下,图的宽度优先遍历使用的是队列,深度优先遍历使用的是栈;
如果要让用栈实现宽度优先遍历、队列实现深度优先遍历,则需要用两个栈实现队列、两个队列实现栈。
3.递归
怎么从思想上理解递归;
怎么从实际实现的角度出发理解递归。
递归的思想是将一个大的任务分解成小的任务,小的任务再进一步拆解,直到达到某一个边界,最后经过某种逻辑进行整合,得到整个问题的求解。
递归调用时,使用了系统栈,调用的函数放入栈,执行完返回时就会从栈顶pop出;
任何递归都可以改为迭代。
有一类递归的时间复杂度可以确定,时间复杂度原始形式如下:
即条件为:子问题的规模是一致的。
时间复杂度公式如下:
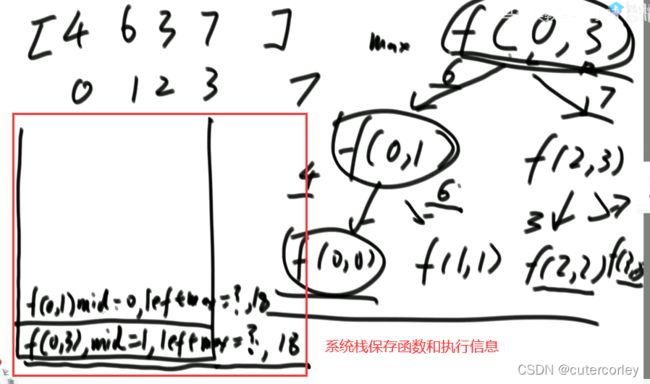
例题:求数组arr[L…R]中的最大值,怎么用递归方法实现。
分析思路:
1)将[L…R]范围分成左右两半。左:[L…Mid]右[Mid+1…R];
2)左部分求最大值,右部分求最大值;
3)[L…R]范围上的最大值,是max{左部分最大值,右部分最大值}。
注意:2)是个递归过程,当范围上只有一个数,就可以不用再递归了。
思路如下:
这里的子问题规模是原问题的一半,所以可以求出时间复杂度,时间复杂度如下:
实现如下:
public class MaxWithRecursion {
public static int getMax(int[] arr) {
return process(arr, 0, arr.length - 1);
}
// arr[L..R]范围上求最大值
public static int process(int[] arr, int L, int R) {
// arr[L..R]范围上只有1个数,直接返回
if (L == R) {
return arr[L];
}
int mid = L + ((R - L) >> 1); // 中点
int leftMax = process(arr, L, mid);
int rightMax = process(arr, mid + 1, R);
return Math.max(leftMax, rightMax);
}
}
4.哈希表和有序表
哈希表
1)哈希表在使用层面上可以理解为—种集合结构;
2)如果只有key、没有伴随数据value,可以使用HashSet结构;
3)如果既有key,又有伴随数据value,可以使用HashMap结构;
4)有无伴随数据,是HashMap和HashSet唯一的区别,实际结构是一回事;
5)使用哈希表增(put)、删(remove)、改(put)和查(get)的操作,可以认为时间复杂度为O(1),但是常数时间比较大;
6)放入哈希表的元素,如果是基础类型,内部按值传递,内存占用是这个元素的大小;
7)放入哈希表的元素,如果不是基础类型(是自定义类型),内部按引用传递,内存占用是8字节(也就是引用地址的大小)。
使用如下:
static class Node {
public int value;
public LinkedList.Node next;
public Node(int data) {
value = data;
}
}
public static void testHashMap() {
// 键值对
HashMap<Integer, String> map = new HashMap<>();
// 新增
map.put(1, "one");
map.put(2, "two");
map.put(3, "three");
map.put(4, "four");
map.put(5, "five");
System.out.println(map.containsKey(1));
System.out.println(map.containsKey(10));
System.out.println(map.containsValue("one"));
System.out.println(map.containsValue("one"));
System.out.println(map.get(1));
System.out.println(map.get(10));
// 修改
map.put(1, "一");
System.out.println(map.get(1));
map.remove(5);
System.out.println(map.get(5));
System.out.println("--------------------");
// 集合元素
HashSet<String> set = new HashSet<>();
set.add("one");
System.out.println(set.contains("one"));
set.remove("one");
System.out.println(set.contains("one"));
System.out.println("--------------------");
// 引用传递和值传递
int a = 10000000;
int b = 10000000;
System.out.println(a == b); // int属于基本数据类型,使用值传递,所以比较时只比较值,不比较地址
Integer c = 10000000;
Integer d = 10000000;
System.out.println(c == d); // Integer属于引用数据类型,使用引用传递,所以比较时比较地址,不比较值,要比较值使用equals方法
System.out.println(c.equals(d));
Integer e = 128;
Integer f = 128;
System.out.println(e == f);
e = 127;
f = 127;
System.out.println(e == f); // -128到127之间,使用常量池,转化为值传递,不在这个区间才使用引用传递
// 新增
map.put(10000, "10000");
System.out.println(map.get(10000));
// 修改
map.put(10000, "一万");
System.out.println(map.get(10000)); // 放入哈希表的元素,如果是基础类型,内部按值传递
HashMap<Node, String> map2 = new HashMap<>();
Node node1 = new Node(1);
Node node2 = new Node(1);
map2.put(node1, "node1");
map2.put(node2, "node1 too");
System.out.println(map2.get(node1));
System.out.println(map2.get(node2));
node2 = node1;
System.out.println(map2.get(node2));
}
输出:
true
false
true
true
one
null
一
null
--------------------
true
false
--------------------
true
false
true
false
true
10000
一万
node1
node1 too
node1
有序表:
有序表指集合内的元素按照某种规则进行排序;
使用哈希表增(put)、删(remove)、改(put)和查(get)的操作,时间复杂度为O(logN)。
AVL、SB树、红黑树和跳表都可以实现有序表,通过调整实现平衡。
使用有序表TreeMap如下:
public static void testTreeMap() {
TreeMap<Integer, String> map = new TreeMap<>();
map.put(3, "three");
map.put(7, "seven");
map.put(2, "two");
map.put(1, "one");
map.put(5, "five");
map.put(9, "nine");
map.put(6, "six");
System.out.println(map.containsKey(1));
System.out.println(map.containsKey(10));
System.out.println(map.get(1));
System.out.println(map.get(10));
// 修改
map.put(5, "五");
System.out.println(map.get(5));
// 删除
map.remove(5);
System.out.println(map.get(5));
// 查看顺序
System.out.println(map.firstKey());
System.out.println(map.lastKey());
System.out.println(map);
// 小于等于5的最近的值
System.out.println(map.floorKey(5));
// 大于等于5的最近的值
System.out.println(map.ceilingKey(5));
}
输出:
true
false
one
null
五
null
1
9
{1=one, 2=two, 3=three, 6=six, 7=seven, 9=nine}
3
6
总结
有很多常用的数据结构,每种数据结构都有适用的场景,可以根据自己的需要进行选择。