算法与数据体系课笔记之-3. 链表结构、栈、队列、递归、哈希表和有序表
目录
- 思维导图链接
- 2.异或运算和几个经典题目分析 总览
-
-
- 题目1:单链表/双链表的反转
-
- 题目描述:
- 代码实现:
- 题目2:[移除链表元素(leetcode链接)](https://leetcode-cn.com/problems/remove-linked-list-elements/)
-
- 题目描述:
- 代码实现:
- 题目3:用双向链表实现队列和栈
-
- 题目描述:
- 代码实现:
- 题目4:用数组实现队列和栈
-
- 题目描述:
- 代码实现:
- 题目5 [包含min函数的栈(leetcode链接)](https://leetcode-cn.com/problems/bao-han-minhan-shu-de-zhan-lcof/)
-
- 题目描述:
- 代码实现:
- 题目6:[用栈实现队列(leetcode链接)](https://leetcode-cn.com/problems/implement-queue-using-stacks/)
-
- 题目描述:
- 代码实现:
- 题目7:[用队列实现栈(leetcode链接)](https://leetcode-cn.com/problems/implement-stack-using-queues/)
-
- 题目描述:
- 代码实现:
- 题目8:获取最大值
-
- 题目描述:
- 代码实现:
-
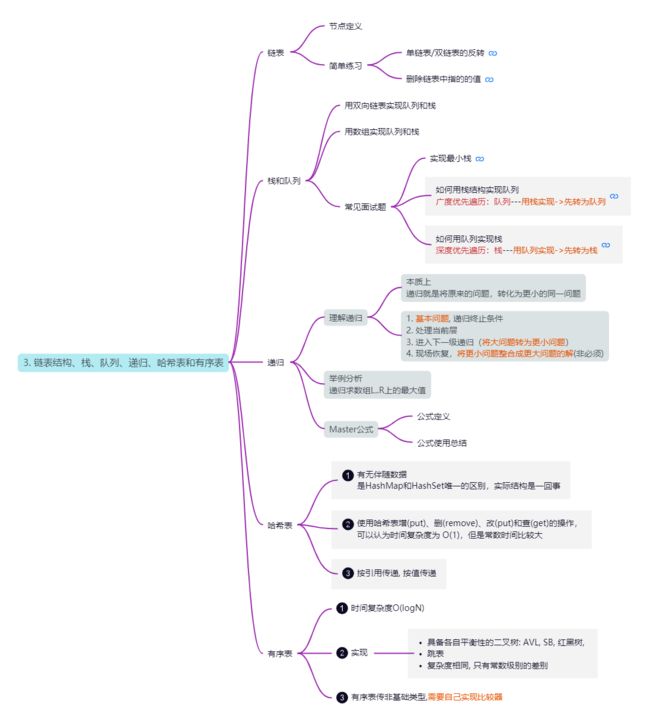
思维导图链接
算法与数据结构思维导图
参考左程云算法课程
2.异或运算和几个经典题目分析 总览
题目1:单链表/双链表的反转
题目链接
题目描述:
- 对指定链表进行反转,并返回新的链表头部
代码实现:
- 节点定义:
package class03;
public class LinkedList {
// 单链表节点的定义
class Node {
// 定义节点值和指针
public int value; // 支持泛型
public Node next; // 指向下个节点的指针
public Node(int value, Node next) {
this.value = value;
this.next = next;
}
public Node(int value) {
this(value, null);
}
public Node() {
this(0, null);
}
}
// 双链表节点的定义
class DoubleNode {
// 定义节点值和双指针
public int value;
public DoubleNode left; // 定义指向前一个节点的左指针
public DoubleNode right; // 定义指向后一个节点的右指针
public DoubleNode(int value, DoubleNode left, DoubleNode right) {
super();
this.value = value;
this.left = left;
this.right = right;
}
public DoubleNode(int value) {
this(value, null, null);
}
public DoubleNode() {
this(0, null, null);
}
}
}
- 反转实现:
package class03;
import class03.LinkedList.DoubleNode;
import class03.LinkedList.Node;
public class Code01_ReverseList {
// 单链表反转
public Node reverseList (Node head) {
Node left = null; // 指向左节点的指针
Node cur = head; // 当前要处理的节点指针
Node right = null;// 指向右节点的指针
while(cur != null) {
// 1. 反转指针指向
right = cur.next; // 先保留好右节点
cur.next = left; // 反转当前节点
// 2. 平移指针,进行下一个节点的反转
left = cur;
cur = right;
}
return left; // 返回最后一个节点,即头节点
}
// 双链表反转
public DoubleNode reverseDoubleList(DoubleNode head) {
DoubleNode left = null;
DoubleNode right = null;
DoubleNode cur = head;
while (cur != null) {
right = cur.right;
cur.right = left;
cur.left = right;
left = cur;
cur = right;
}
return left;
}
}
题目2:移除链表元素(leetcode链接)
题目描述:
- 给你一个链表的头节点
head和一个整数val,请你删除链表中所有满足Node.val == val的节点,并返回 新的头节点 。
代码实现:
package class03;
public class Code02_DeleteGivenValue {
class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int x) {
val = x;
}
}
public ListNode removeElements(ListNode head, int val) {
ListNode dummyHead = new ListNode(); // 定义虚拟头节点
dummyHead.next = head;
ListNode pre = dummyHead; // 寻找目标元素的指针
while(pre.next != null) { // 查找每个元素
if(pre.next.val == val) { // 找到了目标元素,开始处理
ListNode cur = pre.next; // 先将目标元素保存
pre.next = cur.next; // 删除目标元素
cur.next = null; // 将目标元素指向设空,方便垃圾回收
} else { // 如果连续的目标元素均删除完了,就继续找
pre = pre.next;
}
}
// 注意若head删除了,此时dummyHead的next指针已经改变了,
// 指向的是新的头节点
return dummyHead.next;
}
}
题目3:用双向链表实现队列和栈
题目描述:
- 用自定义的双向链表实现队列和栈的基本进出功能,即栈的后进先出,队列的先进先出
代码实现:
package class03;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class Code03_DoubleEndsListToStackAndQueue {
public static class Node<E> {
public E value;
public Node<E> pre;
public Node<E> next;
public Node(E value) {
this.value = value;
}
}
// 自定义有头,尾指针的双向链表
public static class DoubleEndsList<E> {
private Node<E> head; // 指向头节点的指针
private Node<E> tail; // 指向尾节点的指针
// 从头部添加元素
public void addFirst(E value) {
// 1. 先根据节点value,创建节点对象
Node<E> cur = new Node<>(value);
// 2. 向空链表添加节点
if (head == null) {
head = cur;
tail = cur;
// 3. 向非空链表添加元素,注意维护head指针
} else {
// 先建立连接
cur.next = head;
head.pre = cur;
// 再改变头指针指向
head = cur;
}
}
// 从尾部添加元素
public void addlast(E value) {
Node<E> cur = new Node<>(value);
if (head == null) {
head = cur;
tail = cur;
} else {
tail.next = cur;
cur.pre = tail;
tail = cur;
}
}
// 删除头部元素,并返回删除元素节点的值
public E removeFirst() {
// 1. 先处理链表为空的情况
if (head == null)
return null;
// 2. 先保存好要删除的节点元素
Node<E> cur = head;
// 3. 维护头节点指针,将cur的next指向null,方便垃圾回收
// 注意链表中只有一个节点的情况
if (head == tail) {
head = null;
tail = null;
} else {
// 先改变指针指向
head = cur.next;
// 再断了连接
head.pre = null;
cur.next = null;
}
return cur.value;
}
// 删除尾部元素,并返回删除元素节点的值
public E removeLast() {
if (head == null)
return null;
Node<E> cur = tail;
if (head == tail) {
head = null;
tail = null;
} else {
// 先改变指针指向
tail = cur.pre;
// 再断了连接
tail.next = null;
cur.pre = null;
}
return cur.value;
}
public boolean isEmpty() {
return head == null;
}
}
// 用双端链表实现队列
public static class MyQueue<E> {
// 自定义的双端链表作为成员变量
private DoubleEndsList<E> list;
public MyQueue() {
list = new DoubleEndsList<>();
}
// 入队操作
public void push(E value) {
list.addFirst(value);
}
// 出队操作,先进先出,最先进的元素成了链表的尾部元素
public E poll() {
return list.removeLast();
}
public boolean isEmpty() {
return list.isEmpty();
}
}
// 用双端链表实现栈
public static class MyStack<E> {
// 自定义的双端链表作为成员变量
private DoubleEndsList<E> list;
public MyStack() {
list = new DoubleEndsList<>();
}
// 入栈操作
public void push(E value) {
list.addFirst(value);
}
// 出栈操作,后进先出,最后进的元素成了链表的头部元素
public E pop() {
return list.removeFirst();
}
public boolean isEmpty() {
return list.isEmpty();
}
}
// 重定义equals方法
public static boolean isEqual(Integer o1, Integer o2) {
if (o1 == null && o2 != null) {
return false;
}
if (o1 != null && o2 == null) {
return false;
}
if (o1 == null && o2 == null) {
return true;
}
return o1.equals(o2);
}
}
- 代码测试:与java类库中的栈和队列比对测试
public static void main(String[] args) {
int oneTestDataNum = 100;
int value = 10000;
int testTimes = 100000;
for (int i = 0; i < testTimes; i++) {
MyStack<Integer> myStack = new MyStack<>();
MyQueue<Integer> myQueue = new MyQueue<>();
Stack<Integer> stack = new Stack<>();
Queue<Integer> queue = new LinkedList<Integer>();
for (int j = 0; j < oneTestDataNum; j++) {
int nums = (int) (Math.random() * value);
if (stack.isEmpty()) {
myStack.push(nums);
stack.push(nums);
} else {
if (Math.random() < 0.5) {
myStack.push(nums);
stack.push(nums);
} else {
if (!isEqual(myStack.pop(), stack.pop())) {
System.out.println("oops!");
}
}
}
int numq = (int) (Math.random() * value);
if (stack.isEmpty()) {
myQueue.push(numq);
queue.offer(numq);
} else {
if (Math.random() < 0.5) {
myQueue.push(numq);
queue.offer(numq);
} else {
if (!isEqual(myQueue.poll(), queue.poll())) {
System.out.println("oops!");
}
}
}
}
}
System.out.println("finish!");
}
finish!
题目4:用数组实现队列和栈
题目描述:
- 自定义可动态改变容量的动态数组
- 用此数组实现栈和队列的功能
- 用固定的循环数组实现队列功能
代码实现:
package class03;
/**
* 测试用数组实现栈和队列
* @author ls
*
*/
public class Code04_ArraytoStackAndQueue {
/**
* 自定义可改变容量的动态数组,并实现基本增删改查功能
* @author ls
*
* @param 支持泛型
*/
public static class Array<E> {
// 定义成员变量:数组、大小
private E[] data;
private int size = 0;
// 定义构造函数,可以构建指定起始大小的数组
@SuppressWarnings("unchecked")
public Array(int capacity) {
data = (E[]) new Object[capacity]; // 泛型,用基类
}
public Array() {
this(10); // 默认起始容量10
}
// 1. 定义基本方法:获取数组基本信息
// 数组本身对象
public E[] getArray() {
return data;
}
// 数组中已有元素数量
public int getSize() {
return size;
}
// 数组容量
public int getCapacity() {
return data.length;
}
// 是否为空
public boolean isEmpty() {
return size == 0;
}
// 2. 查、找数组中指定索引的元素,时间O(1)
public E getValue(int index) {
checkIndex(index); // // 先判断边界条件
return data[index];
}
private void checkIndex(int index) {
if(index < 0 || index >= size) {
throw new IllegalArgumentException("Get failed. Indext is illegal!");
}
}
public E getFirst() {
return getValue(0);
}
public E getLast() {
return getValue(size-1);
}
// 3. 改、将指定索引元素进行修改,时间O(1)
public void setValue(int index, E value) {
checkIndex(index);
data[index] = value;
}
// 4. 增、向指定索引位置添加元素,注意扩容操作
public void add(int index, E value) {
// 注意:每次增加元素前,先判断数组容量,防止边界溢出
if(size == data.length) {
resize(2 * data.length);
}
if(index < 0 || index > size) { // index == size可以添加
throw new IllegalArgumentException("Get failed. Indext is illegal!");
}
// 指定位置添加不覆盖,需要将其及后的元素后移挪位
for(int i = index; i < size; i ++) { // 容量大于size,i+1=size故不会溢出
data[i + 1] = data[i]; // 但遍历方法需i+1
}
data[index] = value;
size ++; // 切记,一定不要忘记维护size的大小
}
public void addFirst(E value) { // 时间O(n)
add(0, value);
}
public void addLast(E value) { // 均摊复杂度时间O(1)
add(size, value);
}
// 改变容量大小,时间O(n)
// 核心思想是重新开辟一个空间,将原有数组复制
private void resize(int newCapacity) {
@SuppressWarnings("unchecked")
// 1. 建新空间
E[] newData = (E[]) new Object[newCapacity];
// 2. 将旧数组元素copy到新数组中
for(int i = 0; i < size; i ++) {
newData[i] = data[i];
}
// 3. 用旧数组指针指向新数组对象
data = newData;
}
// 5. 删、
// 5.1 删除指定索引位置元素
public E remove(int index) {
checkIndex(index);
if(isEmpty()) {
throw new IllegalArgumentException("can't remove from empty of array!");
}
E res = data[index];
// 删除的逻辑是,将目标索引后面的元素依次往前移一位,覆盖
for(int i = index; i < size - 1; i ++) { // 边界处理
data[i] = data[i + 1];
}
size --; // 同样,不要忘记对size的维护
// 懒惰缩容,防止添加,删除频繁情况下的频繁动容量
if(size == data.length / 4 && data.length / 2 != 0) {
resize(data.length / 2);
}
return res;
}
public E removeFirst() { // O(n)
return remove(0);
}
public E removeLast() { // 均摊O(1)
return remove(size-1);
}
// 5.2 删除指定元素
public void removeElement(E value) {
int index = find(value);
if(index != -1) {
remove(index);
}
}
// 查找指定元素的索引,一般是辅助方法
public int find(E value) {
for(int i = 0; i < size; i ++) {
if(data[i].equals(value)) {
return i;
}
}
return -1;
}
public boolean contains(E e) {
for(int i = 0; i < size; i++) {
if(data[i].equals(e)) return true;
}
return false;
}
// 6. 为了能打印出数组,重写String方法
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append(String.format("Array: size = %d, capacity = %d\n",
size, data.length));
res.append("[");
for(int i = 0; i < size; i ++) {
res.append(data[i]);
if(i != size - 1) {
res.append(",");
}
}
res.append("]");
return res.toString();
}
}
/**
* 用自定义动态数组实现自定义的栈,实现栈接口的常用定义
* @author ls
*
* @param
*/
public static class ArrayStack<E> implements Stack<E>{
private Array<E> arr;
public ArrayStack() {
arr = new Array<>();
}
@Override
public int getSize() {
return arr.size;
}
@Override
public boolean isEmpty() {
return arr.isEmpty();
}
@Override
public void push(E e) {
arr.addLast(e);
}
@Override
public E pop() {
return arr.removeLast();
}
@Override
public E peek() {
return arr.getLast();
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("Stack:");
res.append("[");
for(int i = 0; i < arr.getSize(); i++) {
res.append(arr.getValue(i));
if(i != arr.getSize()-1) {
res.append(",");
}
}
res.append("] Top");
return res.toString();
}
}
public static class ArrayQueue<E> implements Queue<E> {
private Array<E> arr = new Array<>();
@Override
public void add(E e) {
arr.addLast(e);
}
@Override
public E poll() {
return arr.removeFirst();
}
@Override
public E peek() {
return arr.getFirst();
}
@Override
public int getSize() {
return arr.getSize();
}
@Override
public boolean isEmpty() {
return arr.isEmpty();
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("Queue:");
res.append("Front [");
for(int i = 0; i < arr.getSize(); i++) {
res.append(arr.getValue(i));
if(i != arr.getSize()-1) {
res.append(",");
}
}
res.append("] Tail");
return res.toString();
}
}
/**
* 用固定容量大小的循环数组实现队列
*/
public static class RingArrayQueue {
private int[] arr;
private int pushi;// tail
private int polli;// front
private int size;
private final int limit; // 数组容量大小
public RingArrayQueue(int limit) {
arr = new int[limit];
pushi = 0;
polli = 0;
size = 0;
this.limit = limit;
}
public void push(int value) {
if (size == limit) {
throw new RuntimeException("队列满了,不能再加了");
}
size++;
arr[pushi] = value;
pushi = nextIndex(pushi);
}
public int pop() {
if (size == 0) {
throw new RuntimeException("队列空了,不能再拿了");
}
size--;
int ans = arr[polli];
polli = nextIndex(polli);
return ans;
}
public boolean isEmpty() {
return size == 0;
}
// 如果现在的下标是i,返回下一个位置
private int nextIndex(int i) {
return i < limit - 1 ? i + 1 : 0;
}
}
}
- 代码测试
public static void main(String[] args) {
// 测试数组
System.out.println("测试数组: ");
Array<Integer> arr = new Array<>();
for(int i = 0; i < 11; i ++) {
arr.addLast(i);
}
System.out.println(arr);
for(int i = 0; i < 6; i ++) {
arr.removeLast();
}
arr.removeElement(4);
System.out.println(arr);
// 测试栈
System.out.println("测试栈: ");
ArrayStack<Integer> stack = new ArrayStack<Integer>();
for(int i = 0; i < 11; i ++) {
stack.push(i);
}
System.out.println(stack);
System.out.println(stack.pop());
System.out.println(stack.peek());
System.out.println(stack);
// 测试队列
System.out.println("测试队列: ");
ArrayQueue<Integer> queue = new ArrayQueue<>();
for(int i = 0; i < 10; i ++) {
queue.add(i);
}
System.out.println(queue);
System.out.println(queue.poll());
System.out.println(queue);
}
测试数组:
Array: size = 11, capacity = 20
[0,1,2,3,4,5,6,7,8,9,10]
Array: size = 4, capacity = 10
[0,1,2,3]
测试栈:
Stack:[0,1,2,3,4,5,6,7,8,9,10] Top
10
9
Stack:[0,1,2,3,4,5,6,7,8,9] Top
测试队列:
Queue:Front [0,1,2,3,4,5,6,7,8,9] Tail
0
Queue:Front [1,2,3,4,5,6,7,8,9] Tail
题目5 包含min函数的栈(leetcode链接)
题目描述:
- 定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
代码实现:
package class03;
import java.util.Stack;
public class Code05_GetMinStack {
public static class MinStack {
private Stack<Integer> dataStack; // 装数据的栈,用以push,pop
private Stack<Integer> minStack; // 方便取最小值的栈
public MinStack() {
dataStack = new Stack<Integer>();
minStack = new Stack<Integer>();
}
// 添加操作,O(1)
public void push(int x) {
dataStack.push(x);
if(minStack.isEmpty()) { // 注意不能用minStack==null来判断空
minStack.push(x); // 对象不空,但值空也不行
} else {
int min = minStack.peek();
minStack.push(x < min ? x : min);
}
}
// 删除操作,O(1)
public void pop() {
if(dataStack.isEmpty()) {
throw new IllegalArgumentException("error!");
}
dataStack.pop();
minStack.pop();
}
public int top() {
return dataStack.peek();
}
public int min() {
return minStack.peek();
}
}
public static void main(String[] args) {
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
System.out.println(minStack.min()); //返回 -3.
minStack.pop();
System.out.println(minStack.top()); //返回 0.
System.out.println(minStack.min()); //返回 -2.
}
}
题目6:用栈实现队列(leetcode链接)
题目描述:
-
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
- void push(int x) 将元素 x 推到队列的末尾
- int pop() 从队列的开头移除并返回元素
- int peek() 返回队列开头的元素
- boolean empty() 如果队列为空,返回 true ;否则,返回 false
代码实现:
package class03;
import java.util.Stack;
public class Code06_TwoStacksImplementQueue {
public static class MyQueue {
private Stack<Integer> pushStack;
private Stack<Integer> popStack;
public MyQueue() {
pushStack = new Stack<>();
popStack = new Stack<>();
}
// 添加操作,是压入倒push栈,可以触发倒栈工作
public void push(int x) {
pushStack.push(x);
pushToPop();
}
// push向pop栈倒入数据,满足两个条件:
// 1. pop栈为空时才能倒,以防打乱原pop栈的出栈顺序
// 2. push栈一旦倒,就要倒完,以防打乱原push栈数的顺序
private void pushToPop() {
if(popStack.isEmpty()) { // 条件1
while(!pushStack.isEmpty()) { // 条件2
popStack.push(pushStack.pop());
}
}
}
// 删除操作,是从pop栈中弹出,也可触发倒栈工作
public int pop() {
if (pushStack.empty() && popStack.empty()) {
throw new RuntimeException("Queue is empty!");
}
pushToPop(); // 两个栈但凡有一个不为空,倒过后,popStack一定不空
return popStack.pop();
}
public int peek() {
if (pushStack.empty() && popStack.empty()) {
throw new RuntimeException("Queue is empty!");
}
pushToPop();
return popStack.peek();
}
public boolean empty() {
return pushStack.isEmpty() && popStack.isEmpty();
}
}
}
题目7:用队列实现栈(leetcode链接)
题目描述:
-
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
- void push(int x) 将元素 x 压入栈顶。
- int pop() 移除并返回栈顶元素。
- int top() 返回栈顶元素。
- boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
代码实现:
package class03;
import java.util.LinkedList;
import java.util.Queue;
public class Code07_TwoQueueImplementStack {
public static class MyStack {
private Queue<Integer> queue;
private Queue<Integer> help;
public MyStack() {
queue = new LinkedList<Integer>();
help = new LinkedList<Integer>();
}
// 添加、直接在数据queue中添加即可
public void push(int x) {
queue.add(x);
}
// 删除、要将数据导入help栈中,留下最后一个栈顶元素拿出
public int pop() {
if(queue.isEmpty()) return -1;
while(queue.size() > 1) { // 倒数据
help.add(queue.poll());
}
int res = queue.poll(); // 保留要拿出的数据
// 交换指针
Queue<Integer> temp = queue;
queue = help;
help = temp;
return res;
}
// 查询栈顶元素,于pop方法类似
public int top() {
if(queue.isEmpty()) return -1;
while(queue.size() > 1) {
help.add(queue.poll());
}
int res = queue.poll(); // 不是peek,倒数据后容器要清空
help.add(res); // 查看不删除,故查看后要放回队列中
// 交换指针
Queue<Integer> temp = queue;
queue = help;
help = temp;
return res;
}
public boolean empty() {
return queue.isEmpty();
}
}
public static void main(String[] args) {
MyStack stack = new MyStack();
stack.push(1);
stack.push(2);
System.out.println(stack.top());
System.out.println(stack.pop());
System.out.println(stack.pop());
System.out.println(stack.empty());
}
}
2
2
1
true
题目8:获取最大值
题目描述:
- 用递归实现在一个数组中找到最大值
代码实现:
package class03;
/**
* 使用递归求一组数中的最大值
*
* @author ls
*
*/
public class Code08_GetMax {
// 求数组中的最大值
public static int getMax(int[] arr) {
return getMax(arr, 0, arr.length - 1);
}
private static int getMax(int[] arr, int L, int R) {
// 1. 基本问题
if(L >= R) return arr[L];
// 2. 处理当前层
int mid = L + ((R - L) >> 1);
// 3. 将较大问题转为较小问题
int leftMax = getMax(arr, L, mid);
int rightMax = getMax(arr, mid + 1, R);
// 4. 现场恢复,将较小问题组合成较大问题
return Math.max(leftMax, rightMax);
}
public static void main(String[] args) {
int[] arr = {2,4,5,8,3,9,10};
System.out.println(getMax(arr)); // 10
}
}