DES算法Python实现源码
DES介绍
DES是一种对称密钥加密算法,最初由IBM在1970年代开发。DES使用一个56位密钥和一系列置换、替换和异或操作来加密和解密数据。尽管DES被认为是一个强大的加密算法,但是由于其密钥长度较短,目前已经被认为是不安全的,并且已经被更强大的算法如AES所替代。
算法实现流程图
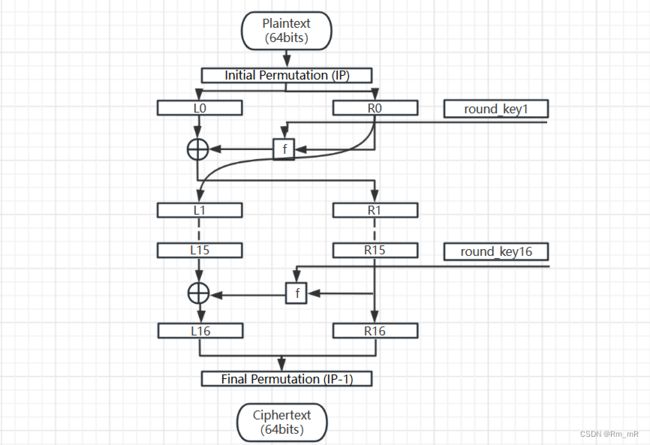
加密算法
密钥扩展算法
64位子密钥通过置换选择1、循环左移以及置换选择2,生成16个48bit的子密钥
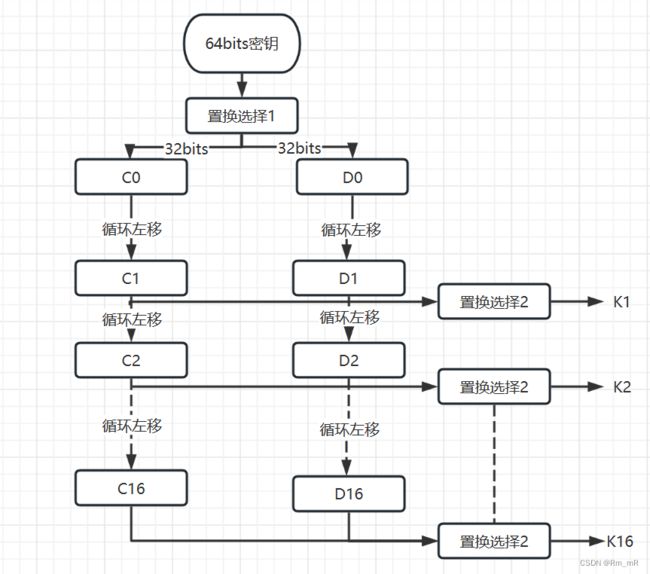
其中循环左移位数与迭代的轮数相关,第1、2、9、16轮循环左移1比特,其余循环左移2比特
源代码
加密算法
IP_table = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7]
IP_table_reverse = [40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
E_table = [32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1
]
S_boxs = [
# 定义8个S盒
# S1盒
[
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
[0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
[4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]
],
# S2盒
[
[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
[3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
[0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
[13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9]
],
# S3盒
[
[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
[13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
[13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
[1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12]
],
# S4盒
[
[ 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
[13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
[10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
[ 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],
],
# S5
[
[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
[14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
[4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
[11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3]
],
#S6盒
[
[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
[10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
[9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
[4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13]
],
# S7盒
[
[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
[13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
[1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
[6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12]
],
# S8盒
[
[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
[1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
[7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
[2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]
]
]
P = [
16,7,20,21,
29,12,28,17,
1,15,23,26,
5,18,31,10,
2,8,24,14,
32,27,3,9,
19,13,30,6,
22,11,4,25
]
PC1 = [57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4]
PC2 = [14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32]
def input_binary(ls, str, length):
while True: # input key
s = input("please input {}(length is {} bit):".format(str, length))
if len(s) != length:
print("the length of {} should be {},please input again:".format(str, length))
else:
break;
for c in s:
ls.append(int(c))
def output_ls(ls, s):
print(s+":")
space = 0
for i in ls:
print(i, end="")
space += 1
if space == 8:
space = 0
print(" ", end="")
print("\n")
def product_transformation(ls, k, od):
"""
:param ls: 乘积变换输入
:param k: 每一轮的轮密钥
:param od: 判断是不是第16轮
:return:
"""
l = ls[0:32]
r = ls[32:64]
s = []
s2 = [0]*32
temp = []
for i in range(0,48): # 选择运算扩展位数
temp.append(r[E_table[i]-1])
temp = [a^b for a,b in zip(temp,k)] # 结果与轮密钥k异或
for i in range(0,8): # 查S盒
index = i*6
row =2*temp[index]+temp[index+5]
col = 8*temp[index+1]+4*temp[index+2]+2*temp[index+3]+temp[index+4]
s_box = S_boxs[i]
a = s_box[row][col]
st = bin(a)[2:]
binary_list = [int(bit) for bit in st]
s1=[0]*(4-len(binary_list))+binary_list
s.extend(s1)
# 置换运算P
for i in range(0,32):
s2[i] = s[P[i]-1]
# 异或运算
xor_list = [a ^ b for a, b in zip(l, s2)] # 结果与Li异或
lis = [0]*32
for i in range(0, 32):
lis[i] = ls[i+32]
ls = ls[32:]+xor_list
return ls
def generate_round_key(ls, round_key):
bit_num = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
ls1 = [0]*56
k = [0]*48
for i in range(0, 56):
ls1[i] = ls[PC1[i]-1] # PC1置换
for i in range(0, 16):
ls1 = ls1[bit_num[i]:28]+ls1[0:bit_num[i]]+ls1[28+bit_num[i]:]+ls1[28:28+bit_num[i]] # 循环左移
for j in range(0, 48):
k[j] = ls1[PC2[j]-1] # PC2置换
round_key.append(k.copy())
def des_encode():
key = [] # 0011000100110010001100110011010000110101001101100011011100111000
M = [] # 0011000000110001001100100011001100110100001101010011011000110111
round_key = []
temp_list = [0]*64
ciphertext = [0]*64
input_binary(M, "plaintext", 64) # 输入明文
input_binary(key, "key", 64) # input 密钥
# sk = "0011000100110010001100110011010000110101001101100011011100111000" # private key
# sm = "0011000000110001001100100011001100110100001101010011011000110111" # plaintext
# for c in sk:
# key.append(int(c))
# for c in sm:
# M.append(int(c))
generate_round_key(key, round_key)
for i in range(0, 64): # IP 置换
temp_list[i] = M[IP_table[i]-1]
for i in range(0, 16):
if i != 15:
od = 0
else:od = 1
temp_list=product_transformation(temp_list,round_key[i],od) # od=1 第16轮特殊处理
temp_list=temp_list[32:]+temp_list[0:32]
for i in range(0, 64):
ciphertext[i] = temp_list[IP_table_reverse[i]-1]
output_ls(ciphertext,"ciphertext:")
des_encode()
解密算法
if i != 15:
od = 0
else: od = 1
temp_list = product_transformation(temp_list, round_key[15-i], od)
相应位置做替换即可
由于DES的运算是对合运算,所以加解密算法相同,只是轮密钥的使用顺序相反,即第一次迭代使用round_key16…第16次使用round_key1。
运行结果
please input plaintext(length is 64 bit):0011000000110001001100100011001100110100001101010011011000110111
please input key(length is 64 bit):0011000100110010001100110011010000110101001101100011011100111000
ciphertext::
10001011 10110100 01111010 00001100 11110000 10101001 01100010 01101101