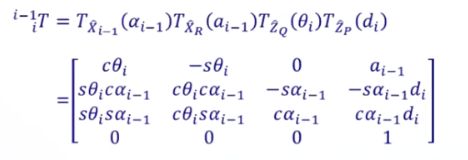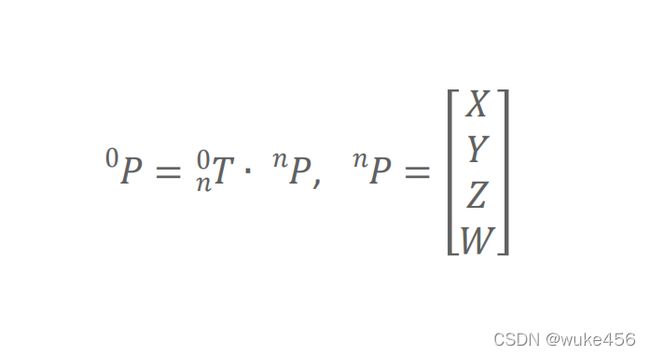三连杆机械臂正运动学python模拟——运动学学习(一)
机械臂运动包含两个问题,一是已知机械臂关节角,求对应的机械臂末端位置和姿态,称为机械臂正运动学;二是已知机械臂末端位置和姿态,求解对应机械臂关节角,称为机械臂逆运动学。
本文通过学习机械臂正运动学的相关知识,使用Python进行三连杆机械臂运动姿态模拟。
求解机械臂正运动学,即已知机械臂各个关节的旋转角度,求解机械臂末端位置与姿态,
可以分为以下几步:
1.在杆件上建立frame(坐标系),用frame状态表示机械臂杆件状态;
2.根据坐标系关系及连杆参数,写出机械臂D-H table;
3.根据D-H table求解出各连杆的变换矩阵T;
4.最后由T矩阵可解出机械臂末端相对于基坐标系的坐标。
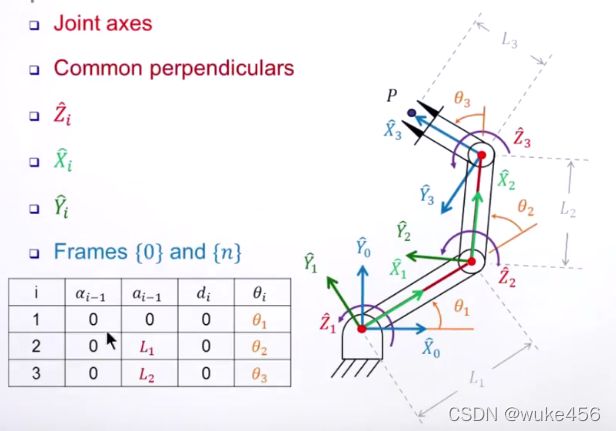
1.1 建立frame
Zi :转动或移动关节的方向;
Xi :沿着ai的方向(ai不为0),
和Zi与Zi+1两者垂直(ai为0);
Yi :与Xi与Zi垂直,遵循右手定则。
1.2 建立D-H参数表
D-H表达法
三连杆各关节坐标系及D-H table 的建立
1.3 坐标变换矩阵T
任意两个关节
连续坐标变换矩阵
1.4 机械臂末端相对基坐标的坐标
其中矩阵中X,Y,Z为机械臂末端位置在frame(n)的坐标,而W取1即可。
1.5 三连杆机械臂正运动学Python模拟
import numpy as np
from math import sin, cos, pi
import matplotlib.pyplot as plt
# Matplotlib是Python的一个绘图库,是Python常用的可视化工具之一
from pylab import mpl
from matplotlib.pyplot import MultipleLocator
class ThreeLinkArm:
"""
三连杆机械臂模拟。
所使用的变量与模拟实体对应关系如下所示:
(joint1)——连杆1——(joint2)——连杆2——[joint3]--连杆3--[tool]
注意:joint1是基座也是坐标原点(0,0)
"""
def __init__(self, _joint_angles=[0, 0, 0]):
self.joint1 = np.array([0, 0])
self.update_joints(_joint_angles)
self.forward_kinematics()
def update_joints(self, _joint_angles): #定义角度更新的方法update_joints()
self.joint_angles = _joint_angles
def transform1(self, _theta1, a0):
self._theta1 = _theta1
self.a0 = a0
T1 = np.mat([
[cos(self._theta1), -sin(self._theta1), 0, 0],
[sin(self._theta1), cos(self._theta1), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
])
return T1
def transform2(self, _theta2, a1):
self._theta2 = _theta2
self.L1 = a1 #杆1长度
T2 = np.mat([
[cos(self._theta2), -sin(self._theta2), 0, self.L1],
[sin(self._theta2), cos(self._theta2), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
])
return T2
def transform3(self, _theta3, a2):
self._theta3 = _theta3
self.L2 = a2 杆2长度
T3 = np.mat([
[cos(self._theta3), -sin(self._theta3), 0, self.L2],
[sin(self._theta3), cos(self._theta3), 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
])
return T3
def forward_kinematics(self): #定义正运动学方法forward_kinematics()
"""
根据各个关节角计算各个关节的位置.
注意:所使用的变量与模拟实体对应关系如下所示:
(joint1)——连杆1——(joint2)——连杆2——[joint3]--连杆3--[tool]
"""
#计算joint1的位置
# q1,q2,q3分别是第1、第2和第3个关节转动的关节角
q1 = self.joint_angles[0]
Q1 = np.mat([[3], #杆1长度为3
[0],
[0],
[1]])
T1 = self.transform1(q1, 0)
joint2 = T1*Q1
x2 = joint2[0, 0]
y2 = joint2[1, 0]
self.joint2 =np.array([x2, y2])
#计算joint2的位置
q2 = self.joint_angles[1]
Q2 = np.mat([[2], #杆2长度为2
[0],
[0],
[1]])
T2 = self.transform2(q2, 3)
joint3 = T1*T2*Q2
x3 = joint3[0, 0]
y3 = joint3[1, 0]
self.joint3 = np.array([x3, y3])
#计算tool的位置
q3 = self.joint_angles[2]
Q3 = np.mat([[1], 杆3长度为1
[0],
[0],
[1]])
T3 = self.transform3(q3, 2)
tool = T1*T2*T3*Q3
x4 = tool[0, 0]
y4 = tool[1, 0]
self.tool = np.array([x4, y4])
def plot(self):
"""
绘制当前状态下的机械臂
"""
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 三个关节的坐标
x = [self.joint1[0], self.joint2[0], self.joint3[0], self.tool[0]]
y = [self.joint1[1], self.joint2[1], self.joint3[1], self.tool[1]]
print(x, y)
plt.plot(x, y, c='black', zorder=1) # 绘制这样的一条线——连杆0————连杆1
plt.scatter(x, y, c='red', zorder=2) # 绘制三个黑圆点代表关节,zorder=2是为了让绘制的点盖在直线上面
plt.title(u'两连杆机械臂正运动学')
plt.xlabel(u'X坐标')
plt.ylabel(u'Y坐标')
x_major_locator = MultipleLocator(1) # 把x轴的刻度间隔设置为1,并存在变量里
y_major_locator = MultipleLocator(1) # 把y轴的刻度间隔设置为1,并存在变量里
ax = plt.gca() # ax为两条坐标轴的实例
ax.xaxis.set_major_locator(x_major_locator) # 把x轴的主刻度设置为0.5的倍数
ax.yaxis.set_major_locator(y_major_locator) # 把y轴的主刻度设置为0.5的倍数
plt.xlim(-5, 5) # 设置x轴的刻度范围
plt.ylim(0, 6) # 设置y轴的刻度范围
plt.show()
arm_robot = ThreeLinkArm([pi/2, pi/4, pi/3])
arm_robot.plot()
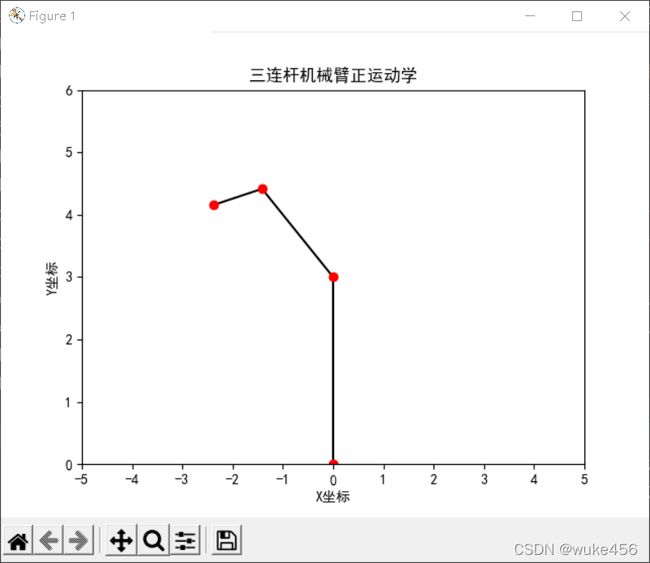
程序可实现“通过修改ThreeLinkArm()中的三个角度变量,绘图显示机械臂姿态变化”
运行结果