【LeetCode力扣】42. 接雨水

目录

1、题目介绍

2、解题思路

2.1、暴力破解法

2.2、双指针法

 

 

1、题目介绍

原题链接： 42. 接雨水 - 力扣（LeetCode）

 示例 1：

 

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
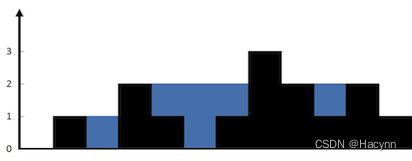
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

 示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

 提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[ i ] <= 105 

2、解题思路

2.1、暴力破解法

首先看到这题的第一反应就是，通过每层遍历去找出蓝色块（即水块）。

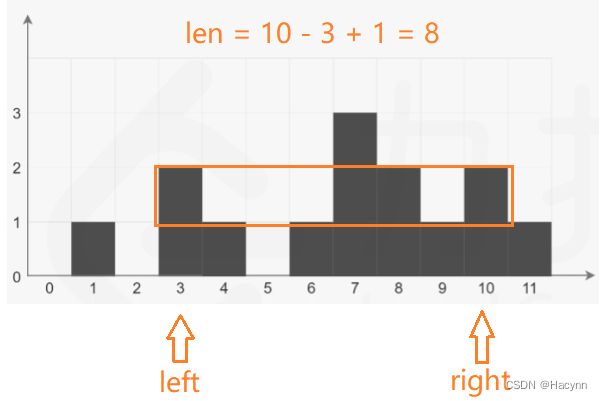
只要找到每一层的边界，再通过右边界right - 左边界left + 1即可得出该层（蓝色块与黑色块）的总和，再通过遍历去掉黑色块，就能够得出单层的水块，最终将每一层水块累加则得出结果。

图解说明： 

第一层：

        通过计算找出第一层的边界，可以发现第一层的边界规律是，只要左边界left从左往右找到第一个大于等于1的柱子，即是左边界；而右边界right从右往左找到第一个大于等于1的柱子，即为右边界。再通过right - left + 1（即11-1+1 = 11）得到第一层所有所有区域总和len，然后从left进行遍历数组到right ，只要当前值大于等于1，则len自减1。最后减完之后得出的len即为第一层水块数。

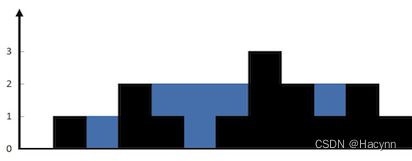
第二层：

        同理，只要左边界left从左往右找到第一个大于等于2的柱子，即是左边界；而右边界right从右往左找到第一个大于等于2的柱子，即为右边界。再通过right - left + 1（即8）得到第二层所有所有区域总和len，然后从left进行遍历数组到right ，只要当前值大于等于2，则len自减1。最后减完之后得出的len即为第二层水块数。

第三层 ：

        当边界left < right 时，循环结束，此时第三层的left等于right，直接退出循环，不需要计算。

 代码实现：

其中：

heightMax方法用于计算整个数组的最大值，也就是最大层数，最大层数有多少，就需要遍历多少次。

layerNumber方法用于计算每一层的水块个数。

class Solution {
    public int trap(int[] height) {
        int left = 0;
        int right = height.length - 1;
        int sum = 0;
        int max = heightMax(height);   //计算出最大层数
        for(int i = 1; i <= max; i++) {  //几层就循环几次
            if(left < right) {
                while(height[left] < i) {   //找出左边界
                    left++;
                }
                while(height[right] < i) {  //找出右边界
                    right--;
                }
                int ret = layerNumber(height,left,right,i);  //计算该层的水块
                sum += ret;  //sum记录水块个数
            }
        }
        return sum;
    }

    public int heightMax(int[] arr) {
        int max = arr[0];
        for(int i = 1; i < arr.length; i++) {
            max = max > arr[i] ? max : arr[i];
        }
        return max;
    }

    signal是当前所在层数
    public int layerNumber(int[] arr, int left, int right, int signal) {   
        int len = right - left + 1;   //画图理解+1
        for(int i = left; i <= right; i++) {
            if(arr[i] >= signal) {
                len--;
            }
        }
        return len;
    }
}

 但是由于是暴力破解，每层都需要依次遍历，因此时间复杂度和空间复杂度非常高。

下面给大家讲解一个巧妙运用双指针在动态规划下快速计算出结果的算法。

2.2、双指针法

leftMax用于记录当前左指针left经过的最大高度，同理rightMax用于记录当前左指针right经过的最大高度。

下标 i 处能否接水以及接到水的数量其实取决于左指针left到 i 时所经过的最大高度leftMax与右指针right到 i 时所经过的最大高度rightMax它们之间的较小值。

例如：

下标5处，它能接到水的数量是leftMax和rightMax的最小值减去下标 i 的高度。

再例如：

下标9处，它能接到水的数量是leftMax和rightMax的最小值减去下标 i 的高度。

代码实现： 

class Solution {
    public int trap(int[] height) {
        int left = 0;
        int right = height.length - 1;
        int leftMax = 0;
        int rightMax = 0;
        int sum = 0;
        while(left < right) {
            leftMax = Math.max(leftMax,height[left]);  //每次循环前判断最大值
            rightMax = Math.max(rightMax,height[right]); //每次循环前判断最大值
            //谁小移动谁，并且移动前计算当前位置与最大高度的差值,差值即水量数。
            if(leftMax > rightMax) {     
                sum += rightMax - height[right];
                right--;
            }else{    //相等时移动哪一个都可以，这里移动left
                sum += leftMax - height[left];
                left++;
            }
        }
        return sum;
    }
}

复杂度分析：

时间复杂度：O(n)，其中 n 是数组 height 的长度。两个指针的移动总次数不超过 n。

空间复杂度：O(1)。只需要使用常数的额外空间。

使用该方法能够大大降低时间复杂度。

更多【LeetCode刷题】推荐：

【LeetCode力扣】189 53 轮转数组 | 最大子数组和-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/134095703?spm=1001.2014.3001.5502

【LeetCode力扣】234 快慢指针 | 反转链表 | 还原链表-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/133958602?spm=1001.2014.3001.5502 

【LeetCode力扣】86. 分隔链表-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/133942678?spm=1001.2014.3001.5502 

 

如果觉得作者写的不错，求给博主一个大大的点赞支持一下，你们的支持是我更新的最大动力！

如果觉得作者写的不错，求给博主一个大大的点赞支持一下，你们的支持是我更新的最大动力！

如果觉得作者写的不错，求给博主一个大大的点赞支持一下，你们的支持是我更新的最大动力！