PyTorch学习（八）--卷积神经网络基础

教程视频：https://www.bilibili.com/video/BV1EE411j78F
这篇文章的所有图片和代码均来自教程的PPT

1、背景
我们输入的图像有三个维度：C(通道数)，W（宽），H（高）。当我们把图像横向展开，变成一维的时候，两个空间上挨着特别近的点，比如（0，3）和（1，3）本来是竖向挨着的，就会距离很远，因为会间隔（0，3）以后（1，3）之前的所有点，所以在做全连接模型的时候就忽略了他们空间上的信息，这也是该模型的一个天花板。这时候卷积就很有用了，他会保留图像的空间结构。

2、通道？
在电脑中看到的大多数图像都是栅格图像，也就是说当你把所看到的图像放大再放大以后，你就会发现你的图像变成了类似于马赛克一样，一个格子一个格子的，事实上你的这些图片也确实是由这些格子组成的，只不过这些格子足够的密，以至于让你区分不开。而每一个格子当中，实际上它有三个变量，Red红色，Green绿色，Blue蓝色。他们的值分别为0~255，这三种颜色以不同的比例混合的时候，它就组成了我们所显示的各种颜色，那么红色绿色蓝色，也就是我们所说的三通道。

当然也不一定必须是三通道，比如黑白照片就可以用单通道来表示，同样也是0~255的区间，如果数值越大则代表颜色越深，那么黑白相片用单通道就可以表示。

所以我们通常理解上的通道数量，就是一个图像中有哪些变量能够决图像的表示，那么这些变量的个数就是通道数。

2、卷积
那么有了通道的概念，大家就可以把一个图像想象为三维结构，它的长和宽就是图像的长和宽高就是通道的个数。

卷积是何如运算的呢？
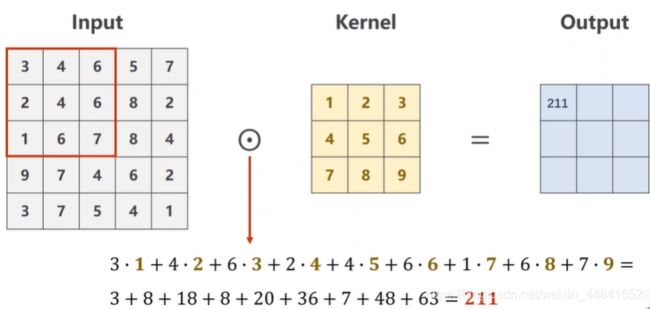
为了举例，我们假设取某一张图片当中绿色通道所有栅格中的值（也就是三维结构的一层）作为输入，也就是下图的Input，我们的卷积核也随便取一个值，比如就是3×3的结构1~9。当开始运算的时候，我们的卷积和定位到输入的左上角，并且根据对应的值进行数乘，以后再相加，作为输出的值。那么算完之后，我们在输入上的框框向右滑动一位，继续按数乘进行运算、求和以此类推。

那么三通道，就是为每一个通道，数乘以它对应的卷积核之后，再将三个经过卷积之后的结果进行对应位置的相加。注意这个时候输出的通道就为1了。

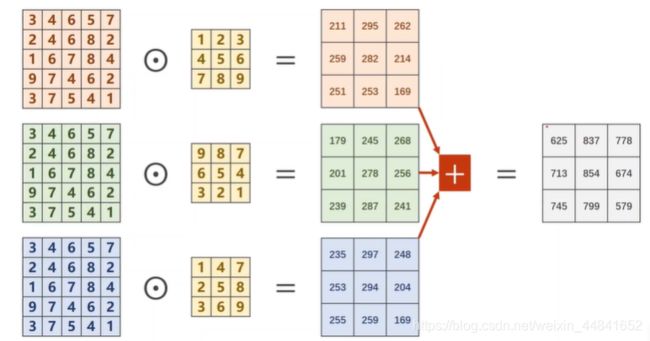
那有人可能就会问了，原来我是三个通道，经过一次转机以后呢，变成了单通道，那如果我的输出需要多通道的话，怎么办呢？很简单，你去找n组，对应的卷积核，再进行多次上图的操作之后把那些，输出的单通道罗列起来又变成了多通道。

总结一下：进行卷积之后C(通道数)，W（宽），H（高）都可能变，当然也可能不变。卷积核通道的数量和输入图片通道的数量是一致的，输出图像的通道数和卷积核的个数是一样的。我们用PyTorch来模拟一下上面的过程

import torch

in_channels, out_channels= 5, 10 #输入和输出的通道数
width, height = 100, 100 #图像大小
kernel_size = 3 #卷积核大小
batch_size = 1

#在torch中输入的数据都是小批量的，所以在输入的时候需要指定，一组有多少个张量
#torch.randn（）的作用是标准正态分布中随机取数，返回一个满足输入的batch，通道数，宽，高的大小的张量
input = torch.randn(batch_size,in_channels,width, height)
#torch.nn.Conv2d（输入通道数量，输出通道数量，卷积核大小）创建一个卷积对象
conv_layer = torch.nn.Conv2d(in_channels,out_channels,kernel_size=kernel_size)
output = conv_layer(input)

print(input.shape)
print(output.shape)
print(conv_layer.weight.shape)

结果：
torch.Size([1, 5, 100, 100])
torch.Size([1, 10, 98, 98])
torch.Size([10, 5, 3, 3])

卷积层还有很多常见的参数：
（1）padding
由上面我们所举的例子可以看出，当一个图片经过3×3的卷积层以后，它的大小会发生改变，长和宽都会缩小一列，那么如果我们想让它经过卷积层以后大小不变怎么办？这个时候就需要用到padding,讲它的作用就是在处理的时候，在原来输出图像外，增加1圈0.这样在进行卷积的时候，输出图像的大小就和输入图像的大小一样了，不信你可以试一下。（当然，如果你愿意也可以增加n圈0）
用PyTorch模拟一下：

import torch

input = [3,4,6,5,7,
         2,4,6,8,2,
         1,6,7,8,4,
         9,7,4,6,2,
         3,7,5,4,1]

#将一个列表转换成一个batch5,通道1，长宽5的张量
input = torch.Tensor(input).view(1, 1, 5, 5)
#卷积层padding=1也就是在外面加一圈
conv_layer = torch.nn.Conv2d(1, 1, kernel_size=3, padding=1, bias=False)
#定义一个卷积核
kernel = torch.Tensor([1,2,3,4,5,6,7,8,9]).view(1, 1, 3, 3)
#我们将自己设置的卷积核权重设置给卷积层的权重
conv_layer.weight.data = kernel.data

output = conv_layer(input)
print(output.data)

结果：（如果你愿意，可以手动算一下）
tensor([[[[ 91., 168., 224., 215., 127.],
[114., 211., 295., 262., 149.],
[192., 259., 282., 214., 122.],
[194., 251., 253., 169., 86.],
[ 96., 112., 110., 68., 31.]]]])

（2）stride(步长)
在之前的例子中，我们在进行了一次卷积运算以后，框框需要往右滑动一位，那么这一位就是他的步长，当然你也可以让他直接向右滑动两位，这个时候就需要stride的这个变量了，结果是这样子的。

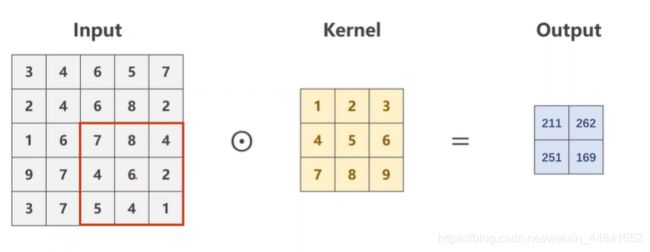
代码实现，一下

import torch

input = [3,4,6,5,7,
         2,4,6,8,2,
         1,6,7,8,4,
         9,7,4,6,2,
         3,7,5,4,1]

input = torch.Tensor(input).view(1, 1, 5, 5)
#stride=2步长调整为2
conv_layer = torch.nn.Conv2d(1, 1, kernel_size=3, stride=2, bias=False)
kernel = torch.Tensor([1,2,3,4,5,6,7,8,9]).view(1, 1, 3, 3)
conv_layer.weight.data = kernel.data

output = conv_layer(input)
print(output.data)

结果：
tensor([[[[211., 262.],
[251., 169.]]]])

（3）下采样
我们图像的输入可能是非常大的，所以需要的进行的运算非常的多，这个时候我们就需要下采样来对图像进行缩小处理，降低运算的需求。下采样中我们用到最多的就是maxpooling最大池化层。

举个例子，比如我们用一个2×2大小的最大池化层，那么它就会在我们输入的图像上分割成n个2×2大小的方格，并且在每一个方格当中取最大值，就像下图这样。通过这样的一次运算，图像的长和宽都缩小为原来的1/2，当然你也可以用规格更大的最大池化层。当我们做下采样的时候通道数是不变的，长宽会变。

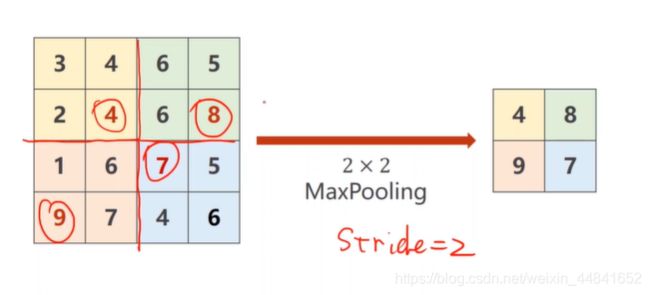
代码实现一下

import torch

input = [3,4,6,5,
         2,4,6,8,
         1,6,7,8,
         9,7,4,6, ]
input = torch.Tensor(input).view(1, 1, 4, 4)

#创建一个2x2的最大池化层
maxpooling_layer = torch.nn.MaxPool2d(kernel_size=2)

output = maxpooling_layer(input)
print(output)

结果：
tensor([[[[4., 8.],
[9., 8.]]]])