Java 实现常用排序算法(未完待续。。。)
java实现常用排序算法
本文只针对内排序:第四版数据结构教程中写:排序过程中,整个表都是放在内存中处理,排序不涉及内,外存数据的交换,则称之为内排序
算法的时间复杂度:
O(1) < O(log2N) < O(n) < O(Nlog2N) < O(n^2) < O(n^3) < O(2^N) < O(N!)
按策略划分排序算法:
一、插入排序
- 直接插入排序
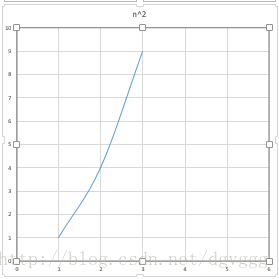
1.直接插入排序(复杂度:O(N^2),稳定)
/*
* 对int[] 的前n位进行 降排序,n应该小于等于数组.length。
*/
public static void InsertSort(int[] a,int n){
//默认数组第一位置是已经排好序的,读数依次从第二位置开始
for(int i= 1; i//保存新获取位置的元素值
int x = a[i];
//新获取位置的前一个位置
int j = i-1;
/*
* 这里进行右边数组加入左边数组的排序处理
*/
//首先判断最新前一位置是否不小于0(防止数组越界),且新获取位置值大于前一位置的值
while(j >=0 && x>a[j]){
//满足条件,则 最新的前一位置的值 赋给 上一次前一位置(如果是第一次while循环,则为 新获取位置的前一个位置的值赋给 新获取位置)
a[j+1] = a[j];
//这里将 前一位置 进行变动,向前推一位
j--;
}
//如果新获取位置的值不再大于 最新前一位置的值,则之前保存的最开始从右边数组取出的值 x 替换 最新前一位置(j) 之后的位置(j+1)!
a[j+1]=x;
}
} - 希尔排序
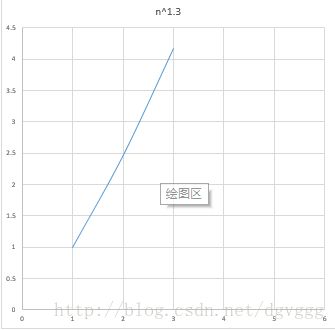
2.增量减半式-希尔排序(复杂度:O(N^1.3),不稳定)
/*
* 对int[] 的前n位进行 降排序,n应该小于等于数组.length。
*/
public static void ShellSort(int[] a,int n){
//初始增量,数组 前n位除 2
int d = n/2;
//对于增量 d 必须满足 最终递减为 1
while(d >= 1){
//下面的循环是以 d 分组之后的组内 插入排序 实现
//默认每个组内的第一位是 已经排序的,所以数组的前 d位,分别为 每个组的 第一位,循环从每个组的第二位开始
for(int i=d;i//保存 某 一组内 新获取位置的元素值
int x = a[i];
//某一组内 新获取位置的 该组内的前一个位置
int j = i-d;
/*
* 这里进行组内 右边数组加入左边数组的排序处理
*/
//首先判断组内最新 前一位置是否不小于0(防止数组越界),且组内新获取位置值大于组内前一位置的值
while(j>=0&&x>a[j]){
//满足条件,则 组内最新的前一位置的值 赋给 组内上一次前一位置(如果是第一次while循环,则为 新获取位置的前一个位置的值赋给 新获取位置)
a[j+d] = a[j];
//这里将组内 前一位置 进行变动,向前推d位
j -= d;
}
//如果组内 新获取位置的值不再大于组内 最新前一位置的值,则之前保存的最开始从组内右边数组取出的值 x 替换 组内最新前一位置(j) 之后的位置(j+d)!
a[j+d] = x;
}
for(int i :a){
System.out.println(i); //打印每次增量变化的输出
}
System.out.println("---------------");
d = d/2; //增量减半
}
} 这里说一下关于希尔排序的简单分析和要求:参考第四版数据结构教程:
首先:希尔排序就是分组的插入排序,即将数据集分组然后组内进行插入排序,增量不为1的排序过程所产生的结果,并不是全数组排序的。
希尔排序的性能分析是个复杂的问题,其时间复杂度是所取增量序列的函数,增量的选取没有定论,但是必须保证增量的最后一位为1。
希尔排序优于插入排序的原因:在希尔排序开始时,增量d较大,分组多,组内数量少,所以各组内的插入排序快。随着增量d变小,组内的数量变多,但是组内的数已接近有序状态,所以新的排序也较快。
- 折半插入排序
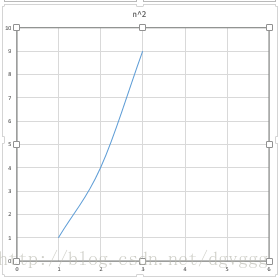
3.折半插入排序(复杂度:O(N^2),稳定)
/*
* 对int[] 的前n位进行 降排序,n应该小于等于数组.length。
*/
public static void BinarySort(int[] a, int n){
//同简单插入相同,首先默认数组第一位属于左边已排序的内容,
for(int i=1;i//确定每次向左边已排序内容插入前,左边内容的第一位和最后一位。以此得到二分需要的初始依赖
int low = 0;
int high = i-1;
//获取将要插入的 值
int x = a[i];
//循环判断 是否 左边的内容 可以继续进行 二分操作,即第一位小于等于最后一位。
while(low <= high){
//计算得二分处理 的中间位置
int mid = (low+high)/2;
//如果 将要 插入的值 比已排序中间位置的值大,则说明 该值应该插入已排序内容的左边
if(x>a[mid]){
//这里更新 二分 需要的最后一位的位置,为上一次中间位置的左一位
high = mid-1;
}
//如果将要插入的值 比已排序中间位置的值小,则说明 该值应该插入已排序内容的右边
else if(x//这里更新二分 需要的第一位的位置,为上一次中间位置的右一位
low = mid+1;
}
System.out.println(high+" "+low);
}
/*
*这里需要注意,二分插入排序 是进行的批量移位(对小于x的数一次性移动,而对于简单插入排序来说:属于循环一次,就可以进行移位的)
*这里小于 x 的 位置内容为:通过上述的二分得到的最终 high+1 到 新插入 数的前一位置
*为什么是 high+1 , -> 二分的最终结果是 low 会大于 high,我们将 x 定位于 high位置的下一位置(即 low 的位置)
*所以可以用 low 直接替换 high+1
关于数组内元素的移位,参考后续补充详解:*/
for(int j=i-1;j>=low;j--){
a[j+1] = a[j];
}
a[low] = x;
for(int y :a){
System.out.println(y);
}
System.out.println("----------------");
}
} 关于数组内元素移动的简单代码实现:
/*
* 移动数组中的元素,即最后一位到第一位,其他元素依次后移 1位
*/
public static void MoveArray2(int[] a,int n){
int x = a[n-1]; //首先直接获取最后一位,保存在x中
for(int i=n-1;i>0;i--){ //从最后一位开始到第二位结束(i>0),依次赋值为其上一位的值
a[i] = a[i-1];
}
a[0] = x;//将保存的x赋给第一位
}折半查找会优于顺序查找,所以就平均性能而言,折半插入排序优于直接插入排序
二、交换排序
- 冒泡排序
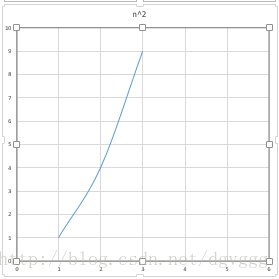
1、冒泡排序(复杂度:O(N^2),稳定)
/*
* 对int[] 的前n位进行 降排序,n应该小于等于数组.length。
* 本例采用向上冒泡方式
*/
public static void BubbleSort(int[] a,int n){
//这里 可以省略最后一趟循环,因为 最后一趟 已经是默认排好序的。
for(int i=0;i1;i++){
//从底层开始向上冒泡,对于前 i 位 是已经排好序的
for(int j=n-1;j>i;j--){
//如果 底层数值 大于上层数值,则进行数值的交换
if(a[j]>a[j-1]){
int temp = a[j-1];
a[j-1] = a[j];
a[j] = temp;
}
}
}
} 改进冒泡排序:
如果在某次循环中,发现数组中元素没有发生一次交换,则可以认为,数组内元素已经排序完成,不需要再进行循环,直接退出。
public static void BubbleSort2(int[] a,int n){
//这里 可以省略最后一趟循环,因为 最后一趟 已经是默认排好序的。
for(int i=0;i1;i++){
//每次循环 默认没有进行数组内数据的交换
boolean exchange = false;
//从底层开始向上冒泡,对于前 i 位 是已经排好序的
for(int j=n-1;j>i;j--){
//如果 底层数值 大于上层数值,则进行数值的交换
if(a[j]>a[j-1]){
int temp = a[j-1];
a[j-1] = a[j];
a[j] = temp;
exchange = true; //如果发生了数据的交换,则对exchange 变量进行修改
}
}
System.out.println(exchange);
if(!exchange){ //如果没有发生数据的交换,则直接可以推出所有循环
break;
}
}
} - 快速排序
2、快速排序(复杂度:O(Nlog2N),不稳定)
/*
* 对int[] 的第low位到第high位进行 降排序,low大于等于0,high小于等于数组.length。
*
* 采用递归方式,每次递归进行的为:左无序集或者右无序集
*/
public static void QuickSort(int[] a,int low,int high){
//首先判断无序集中,是否存在两个及以上的元素
if(low < high){
int i = low;
int j = high;
//获取每次的基准关键字(以此关键字为准,大于关键字的置于左边,小于关键字的置于右边),这里取每个无序集的第一位
int temp = a[low];
//从无序区间的两端开始交替遍历,直到 i=j
while(i!=j){
//首先从 无序集的最后一位(后续为 j-- 多次之后的位置)开始依次向前,判断是否存在大于基准值的,直到出现一个大于基准值的。
//然后使无序集的第一位(后续为 i++ 多次之后的位置) 赋值为 首次大于基准值的值
//如 :6,2,3,9,8,5
while(j>i && temp>=a[j]){
j--;
}
a[i] = a[j];
//8,2,3,9,8,5
//8,9,3,9,2,5
//8,9,3,3,2,5
System.out.println("i:"+i+" ,j:"+j+", value:"+a[i]);
//然后从 无序集的第一位(后续为 i++ 多次之后的位置)开始依次向后,判断是否存在小于基准值的,直到出现一个小于基准值的。
//然后使无序集的首次大于基准值的位置(后续为 j-- 多次之后的位置) 赋值为首次小于基准值的值
while(i//8,2,3,9,2,5
//8,9,3,3,2,5
//8,9,3,3,2,5
System.out.println("i:"+i+" ,j:"+j+", value:"+a[j]);
}
a[i] = temp;
System.out.println("i:"+i+" ,j:"+j+", value:"+a[i]);
for(int n :a){
System.out.print(n);
}
System.out.println();
System.out.println("-------");
//这里递归 的执行顺序为:相当于 树的 先序遍历
QuickSort(a,low,i-1);
QuickSort(a,i+1,high);
}
} 注1:这里需要注意,快速排序采用递归方式每次将元素均匀的分割成两个长度接近的子序列,递归树的高度为O(log2N),所需栈空间为O(log2N)。所以其空间复杂度为O(log2N)。
注2:快速排序使不稳定的排序算法,比如 {5,2,4,8,7,4},这里首先将5作为基准值,则末尾的4会排在2的前面,在进行424的快排过程中,首先会将2的前后的4进行交换,然后剩下24需要再次进行交换,这里交换了两次
三、选择排序
- 直接选择排序
1、直接选择排序(复杂度:O(N^2),不稳定)
/*
* 对int[] 进行 降排序,n小于等于数组.length。
*/
public static void SelectSort(int[] a, int n){
//这里 可以省略最后一趟循环,因为 最后一趟 已经是默认排好序的。
for(int i=0;i1;i++){
//首先获取 数组的第i为默认为最大值位
int k = i;
//循环 第 i+1 位到最后一位,依次与默认最大值位k(i)进行比较,获取到 i 到最后一位的实际最大值位,赋给默认最大值位 k
for(int j=i+1;jif(a[j] > a[k]){
k = j;
}
}
//判断是否最大值位k和第i位相等,不相等就进行交换,将最大值放到第i位,原始i位的值放到最大值位
//这里i是 从第一位到倒数第二位的递增,所以,会将值从大到小排序
if(k!=i){
int max = a[k];
a[k] = a[i];
a[i] = max;
}
}
} 改进直接选择排序:
上述选择排序中,每次循环都会查找出数组中最大的数,然后将数组中的最大数和数组每次循环的起始位置数进行交换。这里我们改进该算法,是通过在每次循环中,选择出最大数与最小数,然后和数组每次循环的起始位置数与末尾位置数进行交换,这样,我们只需要循环数组的一半即可完成排序。
public static void SelectSort2(int[] a, int n){
//由于每次循环都会将 最大和最小数选择出来,所以只需要循环数组一半的次数即可
for(int i=0;i<=(n-1)/2;i++){
//首先获取 数组的第i位(循环开始位置)为默认为最大值位
int k = i;
//同时也默认数组的第 i 位(循环开始位置)为默认最小值位
int v = i;
//循环 第 i+1 位到 n-i 位,依次与默认最大值位k(i)进行比较以及和 默认最小值位v(i)进行比较
//获取到 i+1 到 n-i 的实际最大值 位,赋给默认最大值位 k
//获取到i+1 到 n-i 的实际最小值 位,赋给默认最小值位 v
for(int j=i+1;jif(a[j] > a[k]){
k = j;
continue; //如果 i+1 到 n-i循环过程中,出现大于 k 位置的数, 则该位置的数一定大于v位置数,直接continue
}
if(a[j]//判断是否最大值位k和第i位相等,不相等就进行交换,将最大值放到第i位,原始i位的值放到最大值位
//这里i是 从第一位到倒数第二位的递增,所以,会将值从大到小排序
if(k!=i){
int max = a[k];
a[k] = a[i];
a[i] = max;
for(int s :a){
System.out.print(s);
}
System.out.println();
System.out.println("***********");
}
//判断是否最小值位v和第i位相等,不相等就进行交换,将最小值放到第 n-i-1 位,原始n-i-1位的值放到最小值位
//这里 n-i-1 是每次循环的最后一位
if(v!=i){
int min = a[v];
a[v] = a[n-i-1];
a[n-i-1] = min;
for(int s :a){
System.out.print(s);
}
}
System.out.println();
System.out.println("----------");
}
} - 堆排序