5.6前 K 个高频元素（LC347-M）

算法：

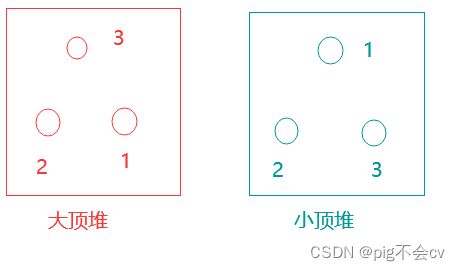
堆：堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。

如果用队列，从大到小排就是大顶堆，从小到大排就是小顶堆。

这道题目主要涉及到如下三块内容：

1. 要统计元素出现频率
2. 对频率排序
3. 找出前K个高频元素

（1）统计元素出现的频率，这一类的问题可以使用dict来进行统计。

（2）然后是对频率进行排序，这里我们可以使用一种 容器适配器就是优先级队列。

什么是优先级队列呢？

其实就是一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。

本题我们就要使用优先级队列来对部分频率进行排序。

所以，可以用优先级队列去遍历dict，优先级队列中保持k个元素，等遍历完以后，优先级队列中的k个元素就是我们要求的。

那么到底用大顶堆还是小顶堆呢？

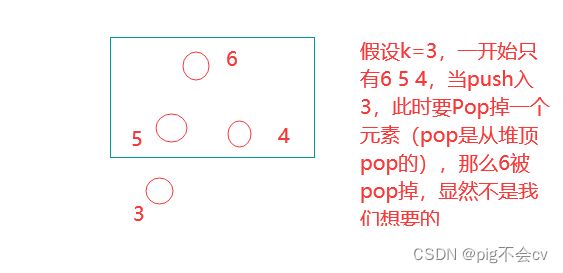
假设用大顶堆

所以，应该用小顶堆。

但是要注意，最后的优先级队列是从小到大排的，而我们输出的结果应该从大到小排，所以要反转一下。而且得取dict中的key作为结果（{key:value}，key是元素，value是频率）

代码里面的新知识：

`heapq` 是 Python 标准库中的模块，提供了对堆（heap）数据结构的实现。

•  `heapq` 模块提供了一些函数来操作堆，包括： 
• `heapify(iterable)`：将可迭代对象转换为堆数据结构。
• `heappush(heap, item)`：将元素插入堆中。
• `heappop(heap)`：从堆中弹出并返回最小的元素。
• `heapreplace(heap, item)`：弹出并返回最小（或最大）的元素，并将新元素插入堆中。
• `nlargest(k, iterable)`：返回可迭代对象中最大的 k 个元素。
• `nsmallest(k, iterable)`：返回可迭代对象中最小的 k 个元素。

注意：以上函数需要通过`heapq`模块调用，比如heapq.heappop(heap)

通过使用 `heapq` 模块，我们可以方便地实现堆排序、获取最大/最小的 k 个元素等操作。 如果您有任何其他问题，请随时提问。

若要实现大顶堆：

有两种方法：
1）先建立小根堆，然后每次heappop()，此时得到从小大的排列，再reverse
2）利用相反数建立大根堆，然后heappop(-元素)。即push(-元素)，pop(-元素)

get函数：

• `map.get(x, 0)`：这是字典的 `get` 方法，用于获取字典中键 `x` 对应的值。如果键不存在，则返回默认值 0。这样做的目的是确保在第一次遇到某个元素时，其对应的值为 0。
• `map[x] = map.get(x, 0) + 1`：这行代码将字典 `map` 中键 `x` 对应的值加 1，并将结果存储回字典中。

map.items()：

map.items()是字典 `map` 的一个方法，用于返回一个包含字典中所有键值对的可迭代对象。每个键值对都表示为一个元组 `(key, value)`。

调试过程：

import heapq
class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        map = {}
        #统计频率
        for i in range(len(nums)):
            map[nums[i]]= map.get(nums[i],0)+1
            #{nums[i]:出现的次数}
        #建立小顶堆
        pri_que = []
        for key, val in map.items():
            #(key,val)以元组的形式放入列表
            pri_que.append((key,val))
            if len(pri_que) > k:
                heapq.heappop(pri_que)
        #倒序取key
        res = []
        #第一个`-1`：这是循环的结束值。循环会一直执行到结束值的前一个位置，即到`-1`为止。在这个例子中，循环会执行到`0`，因为`-1`是结束值的前一个位置。
        #第二个`-1`：这是循环的步长。它表示每次循环迭代时的增量或减量。在这个例子中，步长为`-1`，意味着每次循环迭代时，`i`的值会减少1。
        for i in range(k-1,-1,-1):
        #通过使用索引操作 `[0]`，我们可以获取元组的第1个元素，即 `key`，表示数字。因此，`heapq.heappop(pri_que)[1]`的结果是从小顶堆中弹出的数字。
            res[i]  = heapq.heappop(pri_que)[0]
        return res

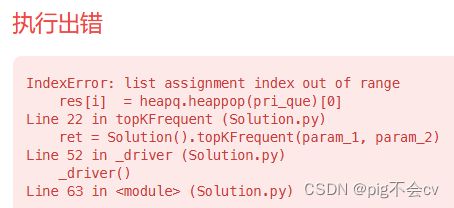
原因：问题出现在这行代码中：`res[i] = heapq.heappop(pri_que)[1]`。在这之前，我们没有将`res`列表初始化为具有足够长度的空列表。因此，无法通过索引直接给`res`列表的元素赋值。

将res=[]改为：res = [0]*k

修改后：

import heapq
class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        map = {}
        #统计频率
        for i in range(len(nums)):
            map[nums[i]]= map.get(nums[i],0)+1
            #{nums[i]:出现的次数}
        #建立小顶堆
        pri_que = []
        for key, val in map.items():
            #(key,val)以元组的形式放入列表
            pri_que.append((key,val))
            if len(pri_que) > k:
                heapq.heappop(pri_que)
        #倒序取key
        res = [0]*k
        #第一个`-1`：这是循环的结束值。循环会一直执行到结束值的前一个位置，即到`-1`为止。在这个例子中，循环会执行到`0`，因为`-1`是结束值的前一个位置。
        #第二个`-1`：这是循环的步长。它表示每次循环迭代时的增量或减量。在这个例子中，步长为`-1`，意味着每次循环迭代时，`i`的值会减少1。
        for i in range(k-1,-1,-1):
        #通过使用索引操作 `[0]`，我们可以获取元组的第1个元素，即 `key`，表示数字。因此，`heapq.heappop(pri_que)[1]`的结果是从小顶堆中弹出的数字。
            res[i]  = heapq.heappop(pri_que)[0]
        return res

原因：

把pri_que.append((key, val))改成heapq.heappush(pri_que, (val, key))，

res[i]  = heapq.heappop(pri_que)[0]改成res[i]  = heapq.heappop(pri_que)[1]就可以了

`heapq.heappush(pri_que, (key, val))` 和 `pri_que.append((val, key))` 是将元素插入小顶堆 `pri_que` 的两种不同方式。

`heapq.heappush(pri_que, (key, val))` 使用 `heapq` 模块的 `heappush` 函数将元组 `(key, val)` 插入到小顶堆 `pri_que` 中。该函数会根据元组中的第一个元素进行比较，并根据比较结果调整堆的结构，以保持小顶堆的性质。

`pri_que.append((val, key))` 直接使用列表的 `append` 方法将元组 `(val, key)` 添加到列表 `pri_que` 的末尾。这样做不会保持小顶堆的性质，需要在后续操作中手动调整堆的结构。

在这个特定的代码中，由于我们要实现一个固定大小为 `k` 的小顶堆，所以每次插入元素后都需要检查堆的大小是否超过 `k`，如果超过则弹出堆顶元素，以保持堆的大小不超过 `k`。使用 `heapq.heappush` 可以自动调整堆的结构，并保证堆顶元素是最小的。而使用 `append` 方法则需要手动调整堆的结构，以确保堆顶元素是最小的。

正确代码：

import heapq
class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        map = {}
        #统计频率
        for i in range(len(nums)):
            map[nums[i]]= map.get(nums[i],0)+1
            #{nums[i]:出现的次数}
        #建立小顶堆
        pri_que = []

        ##用固定大小为k的小顶堆，扫描所有频率的数值
        for key, val in map.items():
            #(key,val)以元组的形式放入列表
            heapq.heappush(pri_que, (val, key))
         
            if len(pri_que) > k:
                heapq.heappop(pri_que)
        #倒序取key
        res = [0]*k
        #第一个`-1`：这是循环的结束值。循环会一直执行到结束值的前一个位置，即到`-1`为止。在这个例子中，循环会执行到`0`，因为`-1`是结束值的前一个位置。
        #第二个`-1`：这是循环的步长。它表示每次循环迭代时的增量或减量。在这个例子中，步长为`-1`，意味着每次循环迭代时，`i`的值会减少1。
        for i in range(k-1,-1,-1):
        #通过使用索引操作 `[1]`，我们可以获取元组的第2个元素，即 `key`，表示数字。因此，`heapq.heappop(pri_que)[1]`的结果是从小顶堆中弹出的数字。
            res[i]  = heapq.heappop(pri_que)[1]
        return res