【AcWing 算法基础课】 2、数据结构 笔记

第二章 数据结构

如果直接用结构体和指针来，每次创建一个新节点就要 new Node(); ，这个操作是非常慢的，如果有非常多数据，如10w，在新建节点的时间就超时了。

所以都是用数组来模拟链表。

STL可以做的，数组都可以做，数组可以做的，STL不一定能做。
所以实现这些数据结构，学习数组的方法，非常重要。

这些模板要熟练掌握，要背下来，需要通过理解来记忆，要能很快的写出相应的模板，学算法时间长的人写代码都很快，并不是他智商高想的快，而是他可以背出来。
就好像我们学习英语，学习古诗，不会在每次写的时候想一想这个单词怎么推理出来，还是需要背下来的。
最终想要学好，需要两点：记忆力和自制力。就像我们学习物理，我们一小时学习的都是前人经过长时间积累所诞生的，不用研究，只需要学习。

平时我们写代码都会有 O2优化，但在比赛中99%都是没有优化的，这个时候纯STL会比数组模拟的数据结构慢一些左右。

一般数据结构都可以快速的维护、支持一些操作。

1、单链表

用的最多的是邻接表。
邻接表最多应用的是存储 图 和 树。

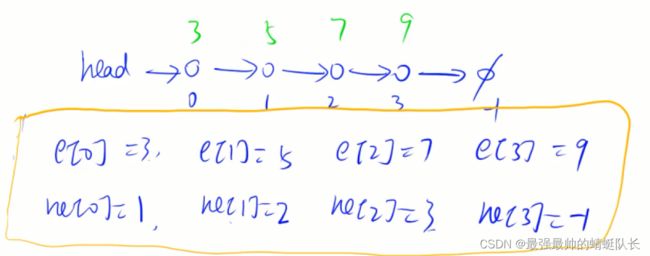
用数组来存储链表。

// head存储链表头，e[]存储节点的值，
// ne[]存储节点的next指针，idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 在链表头插入一个数a
void add_to_head(int a)
{
    e[idx] = a, ne[idx] = head, head = idx ++ ;
}

// 将x插到下标是k的点后面
void add(int k, int x)
{
	e[idx] = x;
	ne[idx] = ne[k];
	ne[k] = idx;
	idx ++;
}

// 将下标是k的点的后面的点删除
void remove(int k)
{
	ne[k] = ne[ne[k]];
}

// 将头结点删除，需要保证头结点存在
void remove()
{
    head = ne[head];
}

2、双链表

用的最多的是优化某些问题。

// e[]表示节点的值，l[]表示节点的左指针，
// r[]表示节点的右指针，idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;

// 初始化
void init()
{
    //0是左端点，1是右端点
    r[0] = 1, l[1] = 0;
    idx = 2;
}

// 在节点a的右边插入一个数x
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

用结构体数组也可以，但是代码会变非常长，数组是最方便的。
以后的最短路问题，最小生成树问题，都是会用到这样数组模拟的邻接表来写的。

邻接表：
就把每个点的所有临边全部存储下来。也就是开了n个单链表，邻接表就是n个单链表

3、栈

先进后出

// tt表示栈顶
int stk[N], tt = 0;

// 向栈顶插入一个数
stk[ ++ tt] = x;

// 从栈顶弹出一个数
tt -- ;

// 栈顶的值
stk[tt];

// 判断栈是否为空
if (tt > 0)
{

}

4、队列

先进先出

1、普通队列

// hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

// 向队尾插入一个数
q[ ++ tt] = x;

// 从队头弹出一个数
hh ++ ;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh <= tt)
{

}

2、循环队列

// hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;

// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;

// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;

// 队头的值
q[hh];

// 判断队列是否为空
if (hh != tt)
{

}

5、单调栈

求序列中每一个数，左边，离他最近且比他小的数在什么地方。

暴力做法：类似双指针，向左遍历，直到第一个小于 i 的值

常见模型：找出每个数左边离它最近的比它大/小的数

可参考以下题解：
https://www.acwing.com/solution/content/27437/

int tt = 0;
for (int i = 1; i <= n; i ++ )
{
	// 栈非空，且栈顶元素是 >= 当前这个数
    while (tt && check(stk[tt], i)) tt -- ; 
    stk[ ++ tt] = i;
}

6、单调队列

求滑动窗口里的最大值和最小值
如以下数据，输出每个窗口的最大值、最小值。

这个窗口就是一个队列，每移动一次就是在队列中入队一个值并出队一个值。
暴力做法就是遍历每一个元素，窗口里有 k 个元素，遍历一遍就是 O(k)，一共有 n 个元素，所有时间复杂度是 O(nk)。如果 n 很大，最后时间是很恐怖的。
优化方式和刚才的单调栈问题是类似的，看一下队列是不是某些元素是没有用的，我们把这些没有用的元素删掉会不会得到单调性。
只要队列里前面一个点比后面的点要大，那么前面一个点就一定没有用，因为后面的点先入队，并且比它小，把这些点删除掉，整个序列就是一个单调上升的序列。

单调栈或者单调队列问题，做法都一样，我们先考虑用栈或者队列，暴力求出结果，然后在看这样的朴素算法中栈和队列哪些元素是没有用的，然后将这些没有用的元素都删掉。
取极值找端点，找一个值用二分。

可参考以下题解：
https://www.acwing.com/solution/content/898/
https://www.acwing.com/solution/content/97229/

// 常见模型：找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;
}

7、KMP

判断子串问题

暴力做法（朴素做法）：

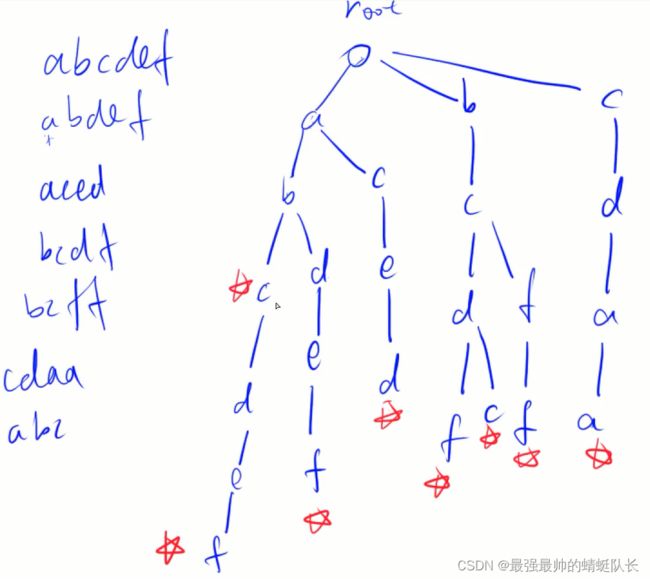
8、Trie 树

高效的存储和查找字符串集合的数据结构

红星表示字符串的结束位置。

int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量

// 插入一个字符串
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++ ;
}

// 查询字符串出现的次数
int query(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

9、并查集

代码很短，但思路比较精巧，比较考验人的思维，所以在笔试、面试、比赛中很常出现。

1、将两个集合合并
2、询问两个元素是否在一个元素当中

belong[x] = a // x 在集合 a 中
if ( belong[x] == belong[y] ) // 判断 x 和 y 是否在同一个集合中

近乎O(1)的时间复杂度之内，快速支持以上操作

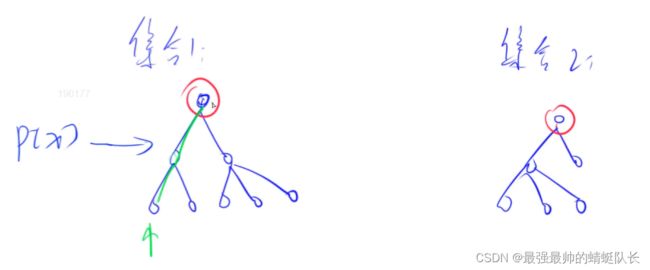
基本原理：
每个集合用一个树来表示，树根的编号就是整个集合的编号。每个节点存储它的父节点，p[x] 表示 x 的父节点。

问题1：如何判断树根：if (p[x] == x)
问题2：如何求 x 的集合编号 ：while(p[x] != x) x = p[x]; // 如果x不是树根，就一直往上走
问题3：如何合并两个集合：p[x] 是 x 的集合编号，p[y] 是 y 的集合编号。p[x] = y;

优化：路径压缩。（按质合并不用）

(1)朴素并查集：

    int p[N]; //存储每个点的祖宗节点

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ ) p[i] = i;

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);


(2)维护size的并查集：

    int p[N], size[N];
    //p[]存储每个点的祖宗节点, size[]只有祖宗节点的有意义，表示祖宗节点所在集合中的点的数量

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        size[i] = 1;
    }

    // 合并a和b所在的两个集合：
    size[find(b)] += size[find(a)];
    p[find(a)] = find(b);


(3)维护到祖宗节点距离的并查集：

    int p[N], d[N];
    //p[]存储每个点的祖宗节点, d[x]存储x到p[x]的距离

    // 返回x的祖宗节点
    int find(int x)
    {
        if (p[x] != x)
        {
            int u = find(p[x]);
            d[x] += d[p[x]];
            p[x] = u;
        }
        return p[x];
    }

    // 初始化，假定节点编号是1~n
    for (int i = 1; i <= n; i ++ )
    {
        p[i] = i;
        d[i] = 0;
    }

    // 合并a和b所在的两个集合：
    p[find(a)] = find(b);
    d[find(a)] = distance; // 根据具体问题，初始化find(a)的偏移量

10、堆

1、插入一个数
2、求集合中的最小值
3、删除最小值
4、删除任意一个元素
5、修改任意一个元素

堆是一个完全二叉树

小根堆：每个点都是 <= 左右儿子的


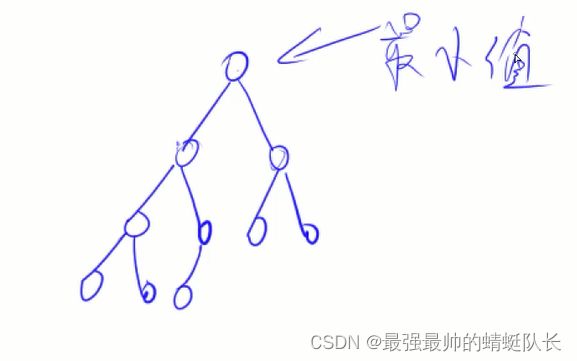
堆排序：时间复杂度为O(1)，详情见视频。

// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;

// 交换两个点，及其映射关系
void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

// O(n)建堆
for (int i = n / 2; i; i -- ) down(i);