八种排序方法(未完待续)
1.冒泡排序(BubbleSort)
是否稳定是指有没有跳转
时间复杂度:O(n^2)
最好:1 2 3 4 5 6 7 8 9 O(n)
最坏:23 45 76 1 6 8 2 O(n^2)
空间复杂度:O(1)
稳定性:稳定排序
从数组的第一个元素开始,如果后一个元素比当前元素小,那么
当前元素往后走,一直重复的遍历这个数组,直至完成
void Bubblesort(int* arr,int len)
{
for(int i=0;iarr[j+1])
{
tmp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=tmp;
swap=true;
}
if(!swap)//说明swap是false;
{
break;
}
}
}
}
1.1图解
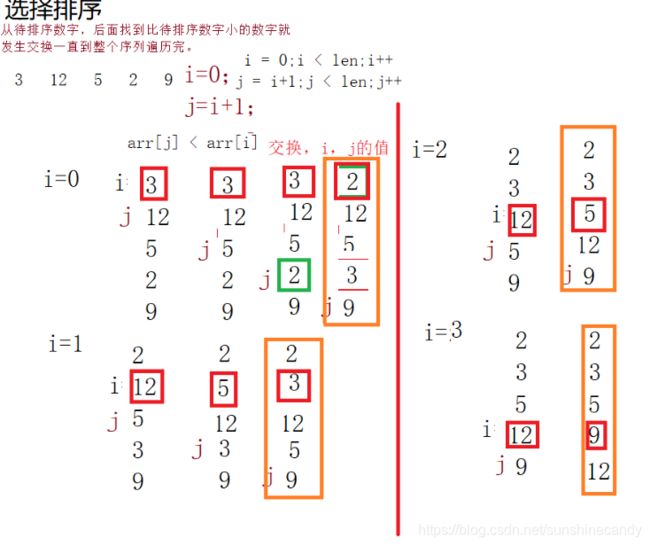
2.选择排序(SelectSort)
选择排序:
从待排序数字,后面找到比待排序数字小的数字就发生交换
一直到整个序列遍历完
时间复杂度: O(n^2)
有序:O(n^2)
无序:O(n^2)
空间复杂度:O(1)
稳定性:不稳定排序
选择排序是一种比较粗暴的方法,首先它有内外两层循环,在每
次的内部循环中都会选定一个数与它后面的每一个数进行比较,将比
它小的与它进行交换,这样就保证了该数是后面所有数中最小的,即
包括该数在内的前面的所有数都是从小到大排列的,在进入第二次循
环时,就选择前一次选择的下一个数,如此循环便可排列。
void SelectSort(int *arr,int len)
{
for(int i = 0;i < len;i++)
{
for(int j = i+1;j < len;j++)
{
if(arr[j] < arr[i])
{
int tmp = arr[j];
arr[j] = arr[i];
arr[i] = tmp;
}
}
}
}
2.2图解
3.插入排序(InsertSort)
直接插入排序:前
时间复杂度: O(n^2)
有序:O(n) 越有序 越快
无序:O(n^2)
空间复杂度:O(1)
稳定性:稳定排序
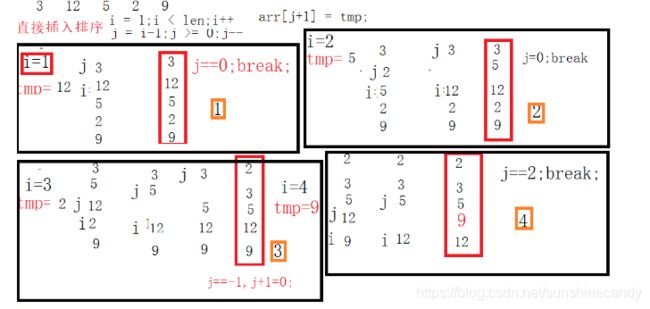
如果有如下一组数字: 4,2,6,5,3 首先当我们在最开始的时候, 4 是
有序的,然后当拿到数据 2 时,我们需要把 2 放到 4 之前,那也就
是说,我们需要让 4 往后移动,然后插入 2 ,以此类推,我们每次
在移动的时候,是比较一个数字,移动一个数字,并且是从后往前移
void InsertSort(int *arr,int len)
{
for(int i = 1;i < len;i++)
{
int tmp = arr[i];
int j = 0;
for(j = i-1;j >= 0;j--)
{
if(arr[j] > tmp)
{
arr[j+1] = arr[j];
}
else
{
break;
}
}
arr[j+1] = tmp;
}
}
3.2图解
4.shell(希尔)排序(ShellSort)
采用分组的思想,先分组,然后在组内插入排序
时间复杂度:有序o(n) 无序(最坏)O(n^2)越有序越快
空间复杂度:O(1)
稳定性:稳定
希尔排序采用分组的思想,把一组数字分为若干的小组,而在分
组的过程当中,并不是几个几个紧挨着的分组,而是采用特定的分租
方式,每一次都让组内有序,这样排序的好处是,每次排序都是将小
的数据尽量往前赶,大的数据尽量往后赶。在这里面,每一组的数字
个数,在一次分组的时候,都会缩小增量,比如第一次每组三个,第
二次每组五个,第三次每组一个这样去分。(最后一次就直接进行一
次插入排序,有点在于,如果不执行前面的分组过程的话,数据的移
动次数更多,更复杂,经过排序之后,数据已经越来越有序了。利用
直接插入排序特性)
好的增量序列的共同特性:
(1)最后一个增量必须为一;
(2)应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。
void Shell(int *arr,int len,int gap)
{
for(int i = gap;i < len;i ++)
{
int tmp = arr[i];
int j = 0;
for(j = i-gap;j >= 0;j = j-gap)
{
if(arr[j] > tmp)
{
arr[j+gap] = arr[j];
}
else
{
break;
}
}
arr[j+gap] = tmp;
}
}
void ShellSort(int *arr,int len)
{
int drr[] = {5,3,1};//每次分的组数
int lend = sizeof(drr)/sizeof(drr[0]);
for(int i = 0;i < lend;i++)
{
Shell(arr,len,drr[i]);
}
}
5.快速排序
快速排序是找出一个元素(理论上可以随便找一个)作为基准
(pivot) ,然后对数组进行分区操作,是基准左边元素的值都不大于基
准,基准右边的元素值都不小于基准,如此作为基准的元素调整到排
序后的真确位置。递归快速排序,将其他 n-1 个元素也调整到排序后
的正确位置。最后每个元素都是在排序后的正确位置,排序完成。所
以快速排序算法的核心算法是分区操作,即如何调整基准的位置以及
调整返回基准的最终位置以便分治递归。
两个变量 int low,int high 分别指向第一个元素和最后一个元素。
再需要一个临时变量,保存每趟基准值。

5.1.固定位置找基准法
5.1.1递归法
时间复杂度:O(nlog2n)最坏O(n^2)最好O(log2n)
空间复杂度:O(log2n)
稳定性:不稳定
int partion(int *arr,int low,int high)//固定位置找基准
{
int tmp=arr[low];
while(lowtmp)//过滤掉比tmp大的数,在后面找比tmp小的数
{
high--;
}
if(low>=high)//说明low到high的后面,退出while(low=high)
{
break;
}
else
{
arr[high]=arr[low];//arr[high]>tmp的挪到后面
//arr [high]=arr[tmp];
}
}
arr [high]=tmp;
return low;
}
void Quick(int *arr,int start,int end)//接着左右两边排序
{
int par = Partion(arr,start,end);//O(n)
//左边
if(par > start+1)
{
Quick(arr,start,par-1);//log2n
}
//右边
if(par < end-1)
{
Quick(arr,par+1,end);
}
}//递归快排
5.1.2.非递归的快速排序!
//非递归实现快速排序
void QuickSort(int *arr,int len)
{
int tmpSize = (int)log((double)len)/log((double)2);
int *stack = (int *)malloc(sizeof(int)*tmpSize*2);//
assert(stack != NULL);
int top = 0;//数组的下标
int low = 0;
int high = len-1;
int par = Partion(arr,low,high);//第一次找完基准
if(par > low +1)
{
stack[top++] = low;
stack[top++] =par-1;
}
if(par < high-1)
{
stack[top++] = par+1;
stack[top++] =high;
}
while(top > 0)//栈不为空
{
high = stack[--top];
low = stack[--top];
par = Partion(arr,low,high);//找完基准
if(par > low +1)
{
stack[top++] = low;
stack[top++] =par-1;
}
if(par < high-1)
{
stack[top++] = par+1;
stack[top++] =high;
}
}
free(stack);
stack = NULL;
}
5.2.随机选取基准法
int partion(int *arr,int low,int high){}//内容见上面的函数
void Swap(int *arr,int start,int end)//交换函数
{
int tmp = arr[start];
arr[start] = arr[end];
arr[end] = tmp;
}//排序方式2:随机选取基准法
void Quick(int *arr, int low, int high)//接着左右两边排序
{
srand((unsigned int)time(NULL));//#include
Swap(arr,low,rand() % (high-low)+low);//rand随机种子
int par = Partion(arr,start,end);//O(n)
//左边
if(par > low+1)
{
Quick(arr,low,par-1);//log2n
}
//右边
if(par < high-1)
{
Quick(arr,par+1,high);
}
}
5.3.三分取中法选取基准
int partion(int *arr,int low,int high){}//内容见上面的函数
void Swap(int *arr,int start,int end){}//交换函数
void SelectPivotMedianOfThree(int *arr,int low,int high) //三分取中法选取基准
{
int mid = (high-low)/2+low;//(high+low)>>1;
//arr[mid]<=arr[low]<=arr[high];
if(arr[mid] > arr[low])
{
Swap(arr,mid,low);
}//arr[mid] <= arr[low]
if(arr[low] > arr[high])
{
Swap(arr,low,high);
}//arr[low] <= arr[high]
if(arr[mid] > arr[high])
{
Swap(arr,mid,high);
}//arr[mid] <= arr[high]
}
void Quick(int *arr, int low, int high)//接着左右两边排序
{
SelectPivotMedianOfThree(arr,low,high);
int par = Partion(arr,start,end);//调用Partion函数
//左边
if(par > low+1)
{
Quick(arr,low,par-1);//log2n
}
//右边
if(par < high-1)
{
Quick(arr,par+1,high);
}
}
5. 4.优化方式(两种)
5.4.1.当待排序的区间中,待排序的个数小于某一个数量级的时候,使用插入排序
int partion(int *arr,int low,int high){}//内容见上面的函数
void InsertSort(int *arr,int low,int high)
{
for(int i = low+1;i <= high;i++)
{
int tmp = arr[i];
int j = 0;
for(j = i-1;j >= low;j--)
{
if(arr[j] > tmp)
{
arr[j+1] = arr[j];
}
else
{
break;
}
}
arr[j+1] = tmp;
}
}
void Quick(int *arr, int low, int high)//接着左右两边排序
{
if((high-low)+1 < 100)
{
InsertSort(arr,low,high);
return;
}
int par = Partion(arr,start,end);//调用Partion函数
//左边
if(par > low+1)
{
Quick(arr,low,par-1);//log2n
}
//右边
if(par < high-1)
{
Quick(arr,par+1,high);
}
}
5.4.2.聚集相同元素基准法
//聚集相同元素基准法
int partion(int *arr,int low,int high){}//内容见上面的函数
void FocusNumPar(int *arr,int low,int par,int high,int *left,
int *right)
{
if(low < high)
{
int parLeft = par-1;
for(int i = par-1;i >= low;i--)
{
if(arr[i] == arr[par])
{
if(i != parLeft)
{
Swap(arr,i,parLeft);
parLeft--;
}
else
{
parLeft--;
}
}
}
*left = parLeft;
int parRight = par+1;
for(int i = par+1;i <= high;i++)
{
if(arr[i] == arr[par])
{
if(i != parRight)
{
Swap(arr,i,parRight);
parRight++;
}
else
{
parRight++;
}
}
}
*right = parRight;
}
}
void Quick(int *arr, int low, int high)
{
int par = Partion(arr,low,high);
int left = 0;
int right = 0;
FocusNumPar(arr,low,par,high,&left,&right);//优化方式2:
if(left >= low+1)//说明左边有两个数据以上
{
Quick(arr,low,left);
}
if(right <= high-1)
{
Quick(arr,right,high);
}
}
6.堆排序
时间复杂度:O(nlog2n)最坏O(nlog2n)最好O(nlog2n)
空间复杂度:O(1)
稳定性:不稳定
void Adjust(int *arr,int start,int end)
{
int tmp = arr[start];
for(int i = 2*start+1;i <= end; i = 2*i+1)
{
//是否有右孩子
if((i < end) && arr[i] < arr[i+1])
{
i++;
}
//i肯定是当前孩子的最大值的下标
if(arr[i] > tmp)
{
arr[start] = arr[i];
start = i;
}
else
{
break;
}
}
arr[start] = tmp;
}
void HeapSort(int *arr,int len)
{
int i = 0;
for(i = (len-1-1)/2;i >= 0;i--)
{
Adjust(arr,i,len-1);
}
//肯定是大根堆
//先交换,后调整(只需要调整0号下标这棵树)
for(i = 0;i < len-1;i++)
{
int tmp = arr[0];
arr[0] = arr[len-1-i];
arr[len-1-i] = tmp;
Adjust(arr,0,len-1-i-1);
}
}
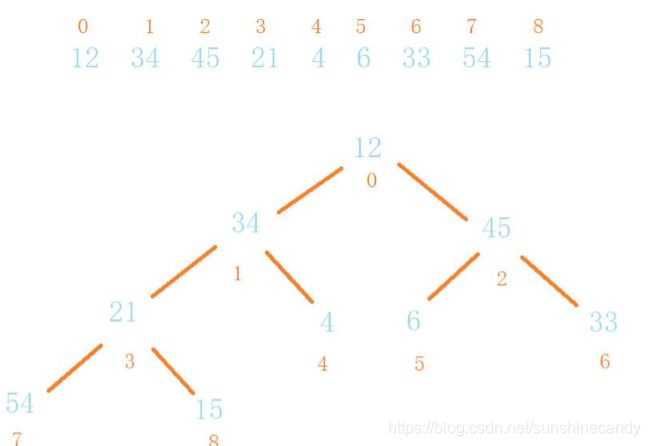
堆是一颗顺序存储的完全二叉树。其中每个节点的关键字都不大
于其孩子节点的关键字,这样的堆称为小根堆(父小于子);其中每
个节点的关键字都不小于其孩子节点的关键字,这样的堆称为大根堆
(父大于子)。因为我们要把数据从小到大排序,所以要建成大根堆。
首先我们需要完成两步:
(1)、调整函数:调整指的是从最后一颗枝丫开始,从上往下调整
(一次调整)。
(2)、然后建立大根堆,而在这个过程当中需要不断的进行调整。
7.归并排序
时间复杂度:O(nlog2n)最坏O(nlog2n)最好O(nlog2n)
空间复杂度:O(n)
稳定性:稳定
void Merge(int *arr,int len ,int gap)
{
int *brr=(int *)malloc(sizeof(int )*len);
assert(brr!=NULL);
int i=0;//i为brr的下标
int start1=0;
int end1=start1+gap-1;
int start2=end1+1;
int end2=start2+gap-1归并排序在八大排序中独占一块,其重要性也是不可小觑的,其
基本思想就是将大块数据分为小块,小块再分小,然后开始排序,其
在实际中也会有应用,例如在面对很庞大数量级的数列进行排序时,
可以将数据分别放入多个文件中,先让各个文件内数据有序,在进行
一次总的排序。
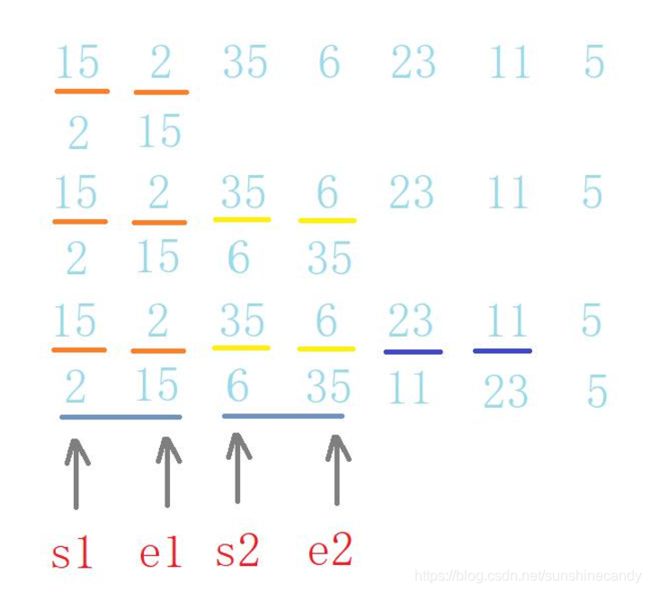
即先使每个子序列有序,再使子序列段间有序。若将两个有序表
合并成一个有序表,称为二路归并。
对于一组数据:15,2,35,6,23,11 其中的每一个数据,单个有序。
然后在进行排序是的两个两个数据有序,以此类推进行排序。
8.基数排序
基数排序:又称“桶子法”排序,他是根据待排序的每一位
上的数字进行入“桶”排序,桶的数量跟当前单个数字的取 值范围有关。当前数字是十进制,单个数字就是 0-9.类似队
列。 如果拿数组实现:那么空间复杂度是 O(rn)//r 桶的数量,n
是数据的个数。
如果把单链表实现:那么没一个桶内的数据,每个数据是一个结点,每个桶都有一个头结点。相对两说更为简单空间复杂度小。
1、单链表的写法
2、确定出桶入桶次数
3、时间复杂度:O(nd),先进先出保证了稳定性
具体操作如下:
第一次入“桶”依据个位的大小进行:
出桶:此时个位已经有序,从桶低开始出
第二次:根据十位进行入“桶”:
出桶:
第三次:根据百位进行入“桶”
出桶:
我们可以看到已经实现了我们从小到大的排序。整个算法实
现,我们用单链表完成。
#include
#include"list.h"
#include
#include
void InitList(List plist)//初始化单链表
{
assert(plist !=NULL );
plist ->data =0;
plist ->next =NULL ;
}
static Node *GetNode(int val)
{
Node* pGet = (Node *)malloc(sizeof(Node));
assert(pGet != NULL);
pGet->data = val;
pGet->next = NULL;
return pGet;
}
bool Insert_tail(List plist,int val)//尾插法
{
Node *cur = plist;//指向头结点 依赖前驱信息的
while(cur->next != NULL)
{
cur = cur->next;
}
Node *pGet = GetNode(val);
cur->next = pGet;
return true;
}
bool IsEmpty(List plist)//是否为空
{
if(plist == NULL || plist->next == NULL)
{
return true;
}
return false;
}
Node *Search_pre(List plist,int key)//查找 key 的前驱
{
if(IsEmpty(plist))
{
return NULL;
}
Node *cur = plist;
while(cur->next != NULL)
{
if(cur->next->data == key)
{
return cur;
}
cur = cur->next;
}
return NULL;
}
bool Delete(List plist,int a)//删除 key 这个结点
{
Node *p = plist ;
if(p == NULL)
{
return false;
}
Node *pDel = p->next;//删除的节点
a=p->data;
p->next = pDel->next;
free(pDel);
pDel = NULL;
return true;
}
bool DeleteFrist(List plist,int *rtv)
{
assert(plist != NULL);
Node *cur = plist->next ;
if(cur == NULL)
{
return false;
}
*rtv = cur ->data ;
plist ->next = cur->next ;
free(cur);
cur = NULL;
return true;
}
int GetMaxBit(int *arr,int len)
{
//1.找到最大值并求出最大值的位数
int max=arr[0];
for(int i=0;imax)
{
max=arr[i];
}
}
int count =0;
while(max!=0)
{
count ++;
max/=10;
}
return count;
}
int GetNum(int num,int figures)//得到figures位是多少
{
for(int i=0;i