通过案例彻底掌握时间复杂度

本篇重点讲解复杂度 以及 常见数据结构的时间复杂度分析，篇幅较长，可以收藏起来慢慢看，感兴趣的跟着小编来一块学习了哈！

1.为什么要进行复杂度分析？

我们先来看下面这个代码，你能评判这个代码的好坏吗？

/**
 * * *求**1~n**的累加和
 * * @param* *n
 * * @return
 */
public int sum(int n) {
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

其实学习算法复杂度的好处就是：

• 指导你编写出性能更优的代码
• 评判别人写的代码的好坏

相信你学完了算法复杂度分析，就有能力评判上面代码的好坏了

关于算法复杂度分析，包含了两个内容，一个是时间复杂度，一个是空间复杂度，通常情况下说复杂度，都是指时间复杂度，我们也会重点讲解时间复杂度

2.时间复杂度

2.1.案例

时间复杂度分析：简单来说就是评估代码的执行耗时的，大家还是看刚才的代码：

/**
 1. * *求**1~n**的累加和
 2. * @param* *n
 3. * @return
 */
public int sum(int n) {
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

分析这个代码的时间复杂度，分析过程如下：

1. 假如每行代码的执行耗时一样：1ms
2. 分析这段代码总执行多少行？3n+3（3n当中的3就是执行一次循环需要执行的代码行数）
3. 代码耗时总时间： T(n) = (3n + 3) * 1ms

T(n):就是代码总耗时

我们现在有了总耗时，需要借助大O表示法来计算这个代码的时间复杂度

2.2.大O表示法

大O表示法：不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势。即字母O代表Order(阶数)。

刚才的代码示例总耗时公式为：T(n) = (3n + 3) * 1ms

其中 (3n + 3) 是代码的总行数，每行执行的时间都一样，所以得出结论：
T(n)与代码的执行次数成正比(代码行数越多，执行时间越长)

不过，大O表示法只需要代码执行时间与数据规模的增长趋势，公式可以简化如下：

T(n) =O(3n + 3)------------> T(n) = O(n)

当n很大时，公式中的低阶，常量，系数三部分并不左右其增长趋势，因此可以忽略，我们只需要记录一个最大的量级就可以了

下图也能表明数据的趋势

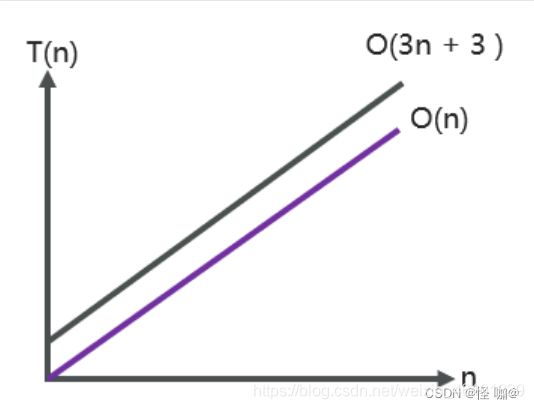
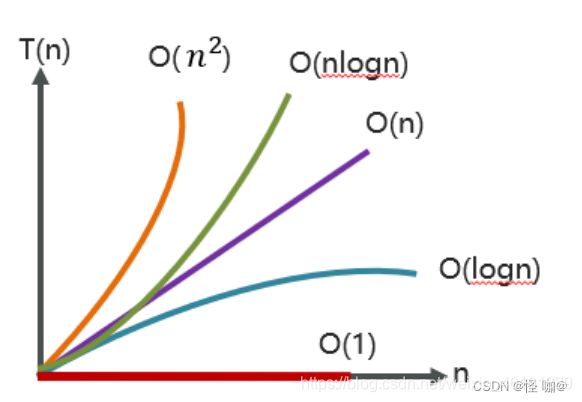
2.3.常见复杂度表示形式

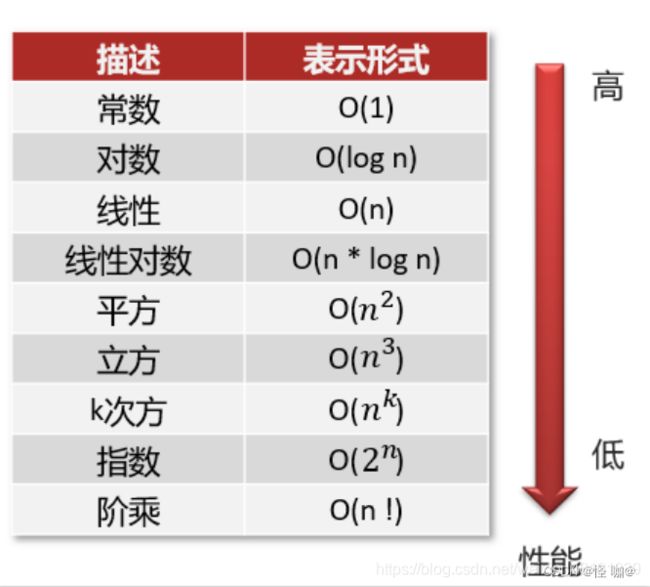
速记口诀：常对幂指阶
越在上面的性能就越高，越往下性能就越低

下图是一些比较常见时间复杂度的时间与数据规模的趋势：

2.4.时间复杂度O(1)

实例代码：

public int test01(int n){
	int i=0;
	int j = 1;
	return i+j;
}

代码只有三行，它的复杂度也是O(1)，而不是O(3)

再看如下代码：

public void test02(int n) {
    int i = 0;
    int sum = 0;
    for (; i < 100; i++) {
        sum = sum + i;
    }
    System.out.println(sum);
}

整个代码中因为循环次数是固定的就是100次，这样的代码复杂度我们认为也是O(1)

一句话总结：只要代码的执行时间不随着n的增大而增大，这样的代码复杂度都是O(1)

2.5.时间复杂度O(n)

实例代码1：

/**
 1. * *求**1~n**的累加和
 2. * @param* *n
 3. * @return
 */
public int sum(int n) {
    int sum = 0;
    for (int i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

一层for循序时间复杂度就是O(n)

实例代码2：

public static int sum2(int n) {
    int sum = 0;
    for (int i = 1; i < n; ++i) {
        for (int j = 1; j < n; ++j) {
            sum = sum + i * j;
        }
    }
    return sum;
}

这个代码的执行行数为：O( 3n^2 + 3n + 3 )，其中3n ^ 2是循环内圈执行行数，3n是循环外圈执行行数，3是循环外的执行行数，不过，依据大O表示的规则：常量、系数、低阶，可以忽略

所以这个代码最终的时间复杂度为：O(n^2)

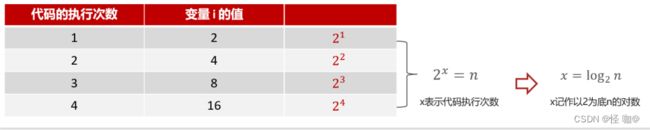
2.6.时间复杂度O(logn)

对数复杂度非常的常见，但相对比较难以分析，实例代码：

public void test04(int n) {
    int i = 1;
    while (i <= n) {
        i = i * 2;
    }
}

分析这个代码的复杂度，我们必须要再强调一个前提：复杂度分析就是要弄清楚代码的执行次数和数据规模n之间的关系

以上代码最关键的一行是： i = i * 2 ，这行代码可以决定这个while循环执行代码的行数， i 的值是可以无限接近 n 的值的。如果 i 一旦大于等于了 n 则循环条件就不满足了。也就说达到了最大的行数。我们可以分析一下 i 这个值变化的过程

分析过程如下：

由此可知，代码的时间复杂度表示为O(log n)

数学常识：

• 阶乘是指从1到给定整数n的所有正整数的乘积，用数学符号表示为n!。例如，5!=1×2×3×4×5=120。
• 平方是一种乘方运算，比如，a的平方表示a×a，简写成a²，电脑上可用^代替，例如x^2就是x²的意思。
• 指数是指一个数的幂，或者说是一个数乘自身的次数。在数学中，a的指数记为a ^ n，其中a叫做底数，n叫做指数。例如，2^3=2×2×2=8。
• 如果a ^ x =N（a>0，且a≠1），那么数x叫做以a为底，N的对数，${\log }_{a}N$ 读作以a为底N的对数，其中a叫做对数的底数，N叫做真数。一般的计算器当中的log计算就是计算的指数，然后底数默认为10，输入的时候输入的是真数。因此计算这类对数时，直接点击计算机的“log”键，再打上数字就可以算出来指数。

2.7.时间复杂度O(n * log n)

分析完O( log n )，那O( n * log n )就很容易理解了，比如下列代码：

public void test05(int n) {
    int i = 0;
    for (; i <= n; i++) {
        test04(n);
    }
}

public void test04(int n) {
    int i = 1;
    while (i <= n) {
        i = i * 2;
    }
}

3.空间复杂度

空间复杂度全称是渐进空间复杂度，表示算法占用的额外存储空间与数据规模之间的增长关系

看下面代码

public void test(int n) {
    int i = 0;
    int sum = 0;
    for (; i < n; i++) {
        sum = sum + i;
    }
    System.out.println(sum);
}

代码执行并不需要占用额外的存储空间，只需要常量级的内存空间大小，因此空间复杂度是O(1)

再来看一个其他例子：

void print(int n) {
   int i = 0;
    int[] a = new int[n];
    for (; i < n; ++i) {
        a[i] = i * i;
    }
    for (i = n - 1; i >= 0; --i) {
        System.out.println(a[i]);
    }
}

传入一个变量n，决定申请多少的int数组空间内存，此段代码的空间复杂度为O(n)

我们常见的空间复杂度就是O(1),O(n),O(n ^2)，其他像对数阶的复杂度几乎用不到，因此空间复杂度比时间复杂度分析要简单的多。

4.数组

4.1.数组寻址公式

数组（Array）是一种用连续的内存空间存储相同数据类型数据的线性数据结构。

int[] array = {22,33,88,66,55,25};

我们定义了这么一个数组之后，在内存的表示是这样的：

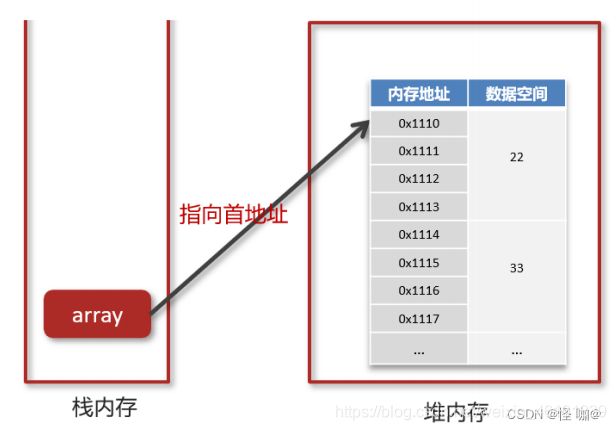
现在假如，我们通过 arrar[1] ，想要获得下标为1这个元素，但是现在栈内存中指向的堆内存数组的首地址，它是如何获取下标为1这个数据的？

为了方便大家理解，我们把数组的内存地址稍微改了一下，都改成了数字，如下图

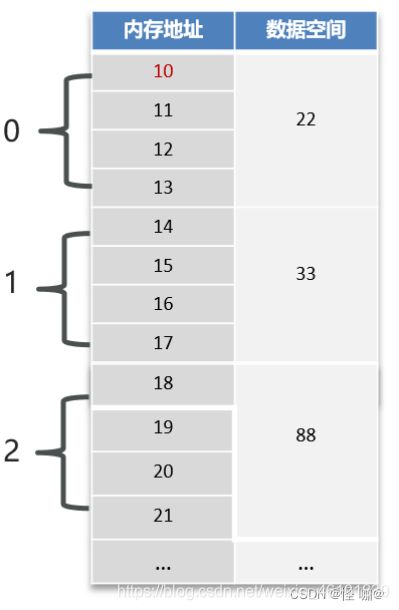
在数组在内存中查找元素的时候，是有一个寻址公式的，如下：

arr[i] = baseAddress + i * dataTypeSize

• baseAddress：数组的首地址，目前是10
• dataTypeSize：代表数组中元素类型的大小，目前数组重存储的是int型的数据，dataTypeSize=4个字节
• arr：指的是数组 i：指的是数组的下标

有了寻址公式以后，我们再来获取一下下标为1的元素，这个是原来的数组

int[] array = {22,33,88,66,55,25};

套入公式：

array[1] =10 + i * 4 = 14

获取到14这个地址，就能获取到下标为1的这个元素了。

4.2.随机查询(根据索引查询)

数组元素的访问是通过下标来访问的，计算机通过数组的首地址和寻址公式能够很快速的找到想要访问的元素

public int test01(int[] a, int i) {
    return a[i];
    // a[i] = baseAddress + i \* dataSize
}

代码的执行次数并不会随着数组的数据规模大小变化而变化，是常数级的，所以查询数据操作的时间复杂度是O(1)

4.3.未知索引查询O(n)或O(log2n)

情况一：查找数组内的元素，查找55号数据，遍历数组时间复杂度为O(n)

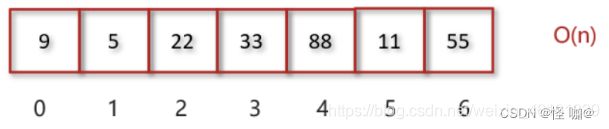
情况二：查找排序后数组内的元素，通过二分查找算法查找55号数据时间复杂度为O(logn)

4.4.插入O(n)

数组是一段连续的内存空间，因此为了保证数组的连续性会使得数组的插入和删除的效率变的很低。

假设数组的长度为 n，现在如果我们需要将一个数据插入到数组中的第 k 个位置。为了把第 k 个位置腾出来给新来的数据，我们需要将第 k～n 这部分的元素都顺序地往后挪一位。如下图所示：

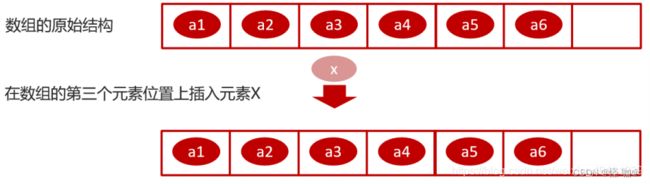
新增之后的数据变化，如下

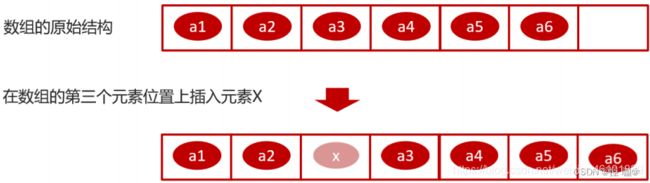
所以：插入操作，最好情况下是O(1)的，最坏情况下是O(n)的，平均情况下的时间复杂度是O(n)。

4.5.删除O(n)

同理可得：如果我们要删除第 k 个位置的数据，为了内存的连续性，也需要搬移数据，不然中间就会出现空洞，内存就不连续了，时间复杂度仍然是O(n)。

5.链表

5.1.单向链表

• 链表中的每一个元素称之为结点（Node）
• 物理存储单元上，非连续、非顺序的存储结构
• 单向链表：每个结点包括两个部分：一个是存储数据元素的数据域，另一个 是存储下一个结点地址的指针域。记录下个结点地址的指针叫作后继指针next

代码实现参考：

链表中的某个节点为B，B的下一个节点为C 表示： B.next==C

5.2.单向链表时间复杂度分析

（1）查询操作

• 只有在查询头节点的时候不需要遍历链表，时间复杂度是O(1)
• 查询其他结点需要遍历链表，时间复杂度是O(n)

（2）插入和删除操作

• 只有在添加和删除头节点的时候不需要遍历链表，时间复杂度是O(1)
• 添加或删除其他结点需要遍历链表找到对应节点后，才能完成新增或删除节点，时间复杂度是O(n)

5.3.双向链表

而双向链表，顾名思义，它支持两个方向

• 每个节点不止有一个后继指针 next 指向后面的结点
• 有一个前驱指针 prev 指向前面的结点

参考代码

对比单链表：

• 双向链表需要额外的两个空间来存储后继结点和前驱结点的地址
• 支持双向遍历，这样也带来了双向链表操作的灵活性

5.4.双向链表时间复杂度分析

（1）查询操作

• 查询头尾结点的时间复杂度是O(1)
• 平均的查询时间复杂度是O(n)
• 给定节点找前驱节点的时间复杂度为O(1)

（2）增删操作

• 头尾结点增删的时间复杂度为O(1)
• 其他部分结点增删的时间复杂度是 O(n)
• 给定节点增删的时间复杂度为O(1)

6.二叉树

6.1.二叉树概述

二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点。

二叉树每个节点的左子树和右子树也分别满足二叉树的定义。

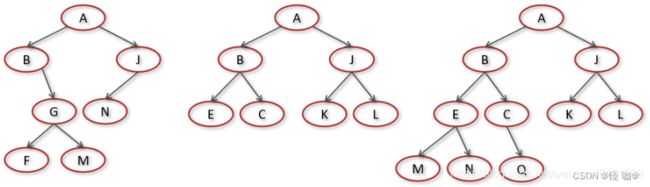
Java中有两个方式实现二叉树：数组存储，链式存储。

基于链式存储的树的节点可定义如下：

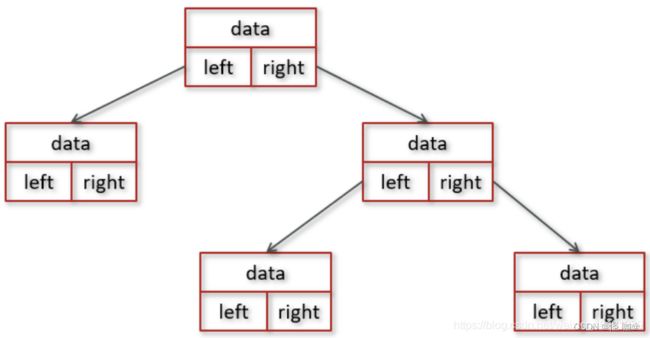
6.2.二叉搜索树

在二叉树中，比较常见的二叉树有：

• 满二叉树
• 完全二叉树
• 二叉搜索树
• 红黑树

我们重点讲解二叉搜索树和红黑树

（1）二叉搜索树概述

二叉搜索树(Binary Search Tree,BST)又名二叉查找树，有序二叉树或者排序二叉树，是二叉树中比较常用的一种类型

二叉查找树要求，在树中的任意一个节点，其左子树中的每个节点的值，都要小于这个节点的值，而右子树节点的值都大于这个节点的值

（2）二叉搜索树-时间复杂度分析

实际上由于二叉查找树的形态各异，时间复杂度也不尽相同，我画了几棵树我们
来看一下插入，查找，删除的时间复杂度

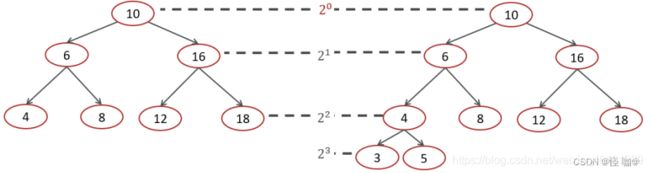
插入，查找，删除的时间复杂度O(logn)

极端情况下二叉搜索的时间复杂度

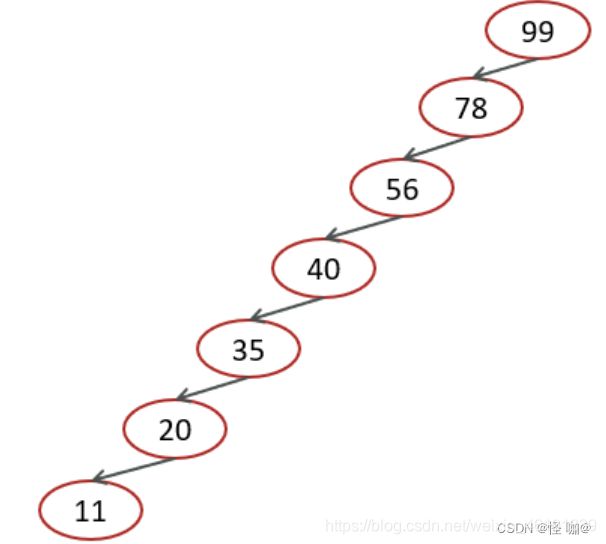
对于图中这种情况属于最坏的情况，二叉查找树已经退化成了链表，左右子树极度不平衡，此时查找的时间复杂度肯定是O(n)。

6.3.红黑树

（1）概述

红黑树（Red Black Tree）：也是一种自平衡的二叉搜索树(BST)，之前叫做平衡二叉B树（Symmetric Binary B-Tree）

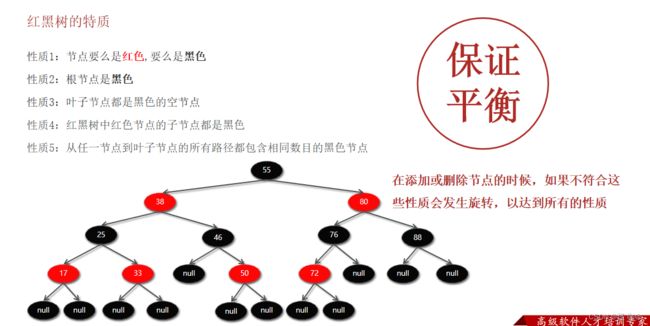
（2）红黑树的特质

（3）红黑树的复杂度

查找：

• 红黑树也是一棵BST（二叉搜索树）树，查找操作的时间复杂度为：O(log n)

添加：

• 添加先要从根节点开始找到元素添加的位置，时间复杂度O(log n)
• 添加完成后涉及到复杂度为O(1)的旋转调整操作
• 故整体复杂度为：O(log n)

删除：

• 首先从根节点开始找到被删除元素的位置，时间复杂度O(log n)
• 删除完成后涉及到复杂度为O(1)的旋转调整操作
• 故整体复杂度为：O(log n)

7.散列表

7.1.散列表（Hash Table）概述

散列表(Hash Table)又名哈希表/Hash表，是根据键（Key）直接访问在内存存储位置值（Value）的数据结构，它是由数组演化而来的，利用了数组支持按照下标进行随机访问数据的特性

举个例子：

假设有100个人参加马拉松，编号是1-100，如果要编程实现根据选手的编号迅速找到选手信息？

可以把选手信息存入数组中，选手编号就是数组的下标，数组的元素就是选手的信息。

当我们查询选手信息的时候，只需要根据选手的编号到数组中查询对应的元素就可以快速找到选手的信息，如下图：

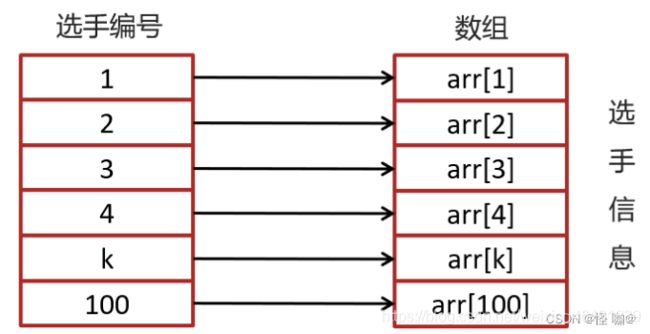
现在需求升级了：

假设有100个人参加马拉松，不采用1-100的自然数对选手进行编号，编号有一定的规则比如：2023ZHBJ001，其中2023代表年份，ZH代表中国，BJ代表北京，001代表原来的编号，那此时的编号2023ZHBJ001不能直接作为数组的下标，此时应该如何实现呢？

我们目前是把选手的信息存入到数组中，不过选手的编号不能直接作为数组的下标，不过，可以把选手的选号进行转换，转换为数值就可以继续作为数组的下标了？

转换可以使用散列函数进行转换

7.2.散列函数和散列冲突

将键(key)映射为数组下标的函数叫做散列函数。可以表示为：hashValue = hash(key)

散列函数的基本要求：

• 散列函数计算得到的散列值必须是大于等于0的正整数，因为hashValue需要作为数组的下标。
• 如果key1==key2，那么经过hash后得到的哈希值也必相同即：hash(key1) ==hash(key2）
• 如果key1 != key2，那么经过hash后得到的哈希值也必不相同即：hash(key1) != hash(key2)

实际的情况下想找一个散列函数能够做到对于不同的key计算得到的散列值都不同几乎是不可能的，即便像著名的MD5,SHA等哈希算法也无法避免这一情况，这就是散列冲突(或者哈希冲突，哈希碰撞，就是指多个key映射到同一个数组下标位置)

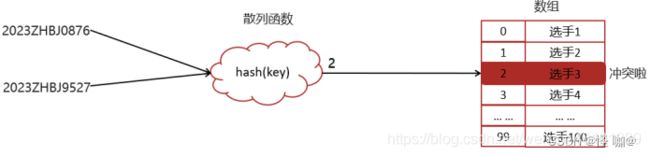
7.3.散列冲突-链表法（拉链）

在散列表中，数组的每个下标位置我们可以称之为桶（bucket）或者槽（slot），每个桶(槽)会对应一条链表，所有散列值相同的元素我们都放到相同槽位对应的链表中。

简单就是，如果有多个key最终的hash值是一样的，就会存入数组的同一个下标中，下标中挂一个链表存入多个数据

7.4.时间复杂度-散列表

（1）插入操作，通过散列函数计算出对应的散列槽位，将其插入到对应链表中即可，插入的时间复杂度是 O(1)

通过计算就可以找到元素

（2）当查找、删除一个元素时，我们同样通过散列函数计算出对应的槽，然后遍历链表查找或者删除

• 平均情况下基于链表法解决冲突时查询的时间复杂度是O(1)
• 散列表可能会退化为链表,查询的时间复杂度就从 O(1) 退化为 O(n)

将链表法中的链表改造为其他高效的动态数据结构，比如红黑树，查询的时间复杂度是 O(logn)

大量的数据项被映射到同一个位置，会导致哈希表的性能急剧下降，容易成为DDoS攻击的目标。红黑树实现哈希表可以提高哈希表的性能，从而增强系统的抗DDoS攻击能力。

DDos 攻击:
分布式拒绝服务攻击(英文意思是Distributed Denial of Service，简称DDoS）指处于不同位置的多个攻击者同时向一个或数个目标发动攻击，或者一个攻击者控制了位于不同位置的多台机器并利用这些机器对受害者同时实施攻击。由于攻击的发出点是分布在不同地方的，这类攻击称为分布式拒绝服务攻击，其中的攻击者可以有多个

8.排序算法复杂度

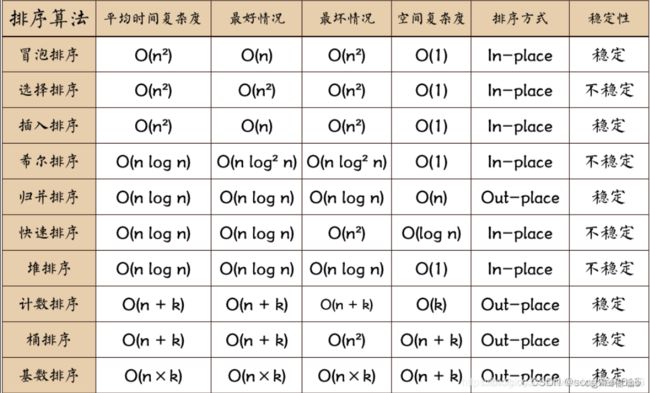
9.总结

（1）数组

• 根据索引查询：O(1)
• 根据元素查询：O(n)
• 根据元素查询，但是数组是有序的可以使用二分查找：O(${\log }_{2}N$)
• 根据索引进行插入，需要移动元素：O(n)
• 根据索引进行删除，需要移动元素：O(n)

（2）链表

• 不论是根据索引还是根据元素查询都需要遍历：O(n)
• 添加或删除其他结点需要遍历链表找到对应节点后，才能完成新增或删除节点，时间复杂度是：O(n)
• 给定节点增删的时间复杂度为：O(1)

（3）有序二叉树

• 插入，查找，删除的时间复杂度O(logn)

（4）散列表

• 插入查询删除操作都是：O(1)
• 散列冲突假如使用链表就是：O(n)
• 散列冲突假如使用红黑树就是：O(${\log }_{2}N$)