六维空间向量表示法公式笔记

目前对机器人动力学还没有一套标准的表示法，比如有3D向量、齐次矩阵、六维空间向量等。其中最有效的是六维空间向量（ Spatial Vector Notation），本文是我看《Handbook of robotics》的笔记，其中看起来弯弯曲曲的字母 $vf$表示3维向量，看起来直直的v f 表示六维空间向量。

1、运动和力

为了区分刚体的运动（motion）和施加在刚体上的力（force），分别用运动六维向量空间$M^6$和力六维向量空间$F^6$来表示。两个空间及其各自的基向量如下图所示

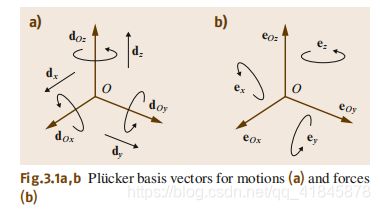
两个空间共有12个基向量，6个用来描述运动，6个用来描述力。

在运动六维空间，对于一个坐标系$O_{xyz}$，三个描述分别绕坐标轴$O_x$，$O_y$，$O_z$进行旋转的基向量$d_{Ox}$，$d_{Oy}$，$d_{Oz}$；三个描述分别沿着坐标轴$O_x$，$O_y$，$O_z$进行平移的基向量$d_x$，$d_y$，$d_z$。

在力六维空间，对于一个坐标系$O_{xyz}$，三个描述分别绕坐标轴$O_x$，$O_y$，$O_z$进行旋转的基向量$e_{Ox}$，$e_{Oy}$，$e_{Oz}$；三个描述分别沿着坐标轴$O_x$，$O_y$，$O_z$进行平移的基向量$e_x$，$e_y$，$e_z$。

2、空间速度和空间力

任意给定一个参考点$O$，刚体的速度可以用一对3维向量来表示：沿三个轴的线速度$v=(v_{Ox},v_{Oy},v_{Oz})$、绕三个轴旋转的角速度$w=(w_x,w_y,w_z)$。那么该运动的六维空间表示法为

相应的其普吕克坐标表示为

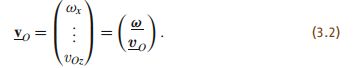
关于力是相似的。刚体受到力$f$和扭矩$n_O$的作用，则该受力情况的六维空间向量表示法为

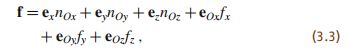
相应的其普吕克坐标表示为

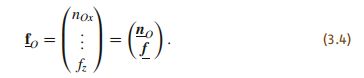
3、加法运算和模乘

如果刚体同时受到两个力f${}_1$和f${}_2$的作用，那么这两个力的合力为f${}_1$+f${}_2$；

如果刚体1的速度为v${}_1$，刚体2的速度为v${}_2$，那么刚体2相对于刚体1的运动速度为v${}_2$-v${}_1$；

如果刚体受到力f${}_1$的作用，其大小为1N，那个$\alpha$f${}_1$表示在该方向上大小为$\alpha$N的力。

4、点积(内积)

六维空间向量的点积定义为该物体的运动m∈M${}^6$和力f∈F${}^6$的点积——f·m或者m·f。

m·m和f·f是无定义的。

如果m和f是用同一坐标系来表示的，那么m·f=m${}^T$f。

5、坐标变换

定义$A$和$B$是两个坐标系，在$A$坐标系下的运动和力分别表示为m${}_A$和f${}_A$；在$B$坐标系下的运动和力分别表示为m${}_B$和f${}_B$。
那么从$A$坐标系下的运动变换到$B$坐标系下的方程为

相应的力的变换为

其中${}^B{X}_A$和${}^B{X}_A^F$分别是从坐标系$A$到坐标系$B$的运动变换矩阵和力变换矩阵。并且二者满足如下关系，也就是从力变换矩阵到运动变换矩阵的变换(或者反过来)是先求逆再转置(求逆和转置可交换)。

假设坐标系$A$相对于坐标系$B$的位置向量为${}^B{p}_A$，旋转变换矩阵为${}^B{R}_A$，那么${}^B{X}_A$可以表示为

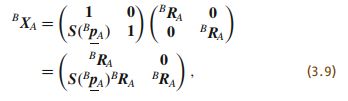
其逆矩阵为

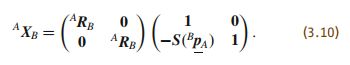
其中$S(p)$为$p$的斜对称矩阵

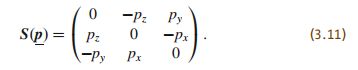
6、叉积(向量积，外积)

六维空间向量的叉积有两种形式，一种是运动和运动做叉积

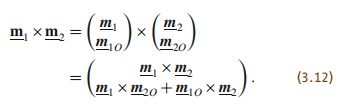
第二种是运动和力做叉积

在此定义一个叉积算子

所以运动和运动的叉积表示为m${}_1$×m${}_2$=S(m${}_1$)m${}_2$

但是运动和力的叉积表示为m×f= - S(m)${}^T$f

可见S(m)将运动向量映射为运动向量，S(m)${}^T$将力向量映射为力向量。

7、微分

六维空间向量的微分定义为

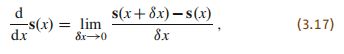
对于一个运动的坐标系$A$，任意的六维空间向量s，该空间向量的微分表示为

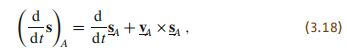
且

8、加速度

六维空间向量的加速度和经典的刚体的加速度是不一样的。

上式中，左式为空间向量的加速度，右式为经典的刚体加速度，两者之间存在如下关系

如果r是某一个刚体相对于任意一个固定点的位置向量，那么存在如下关系

上式中，第一个式子是刚体的速度，第二个式子是刚体的经典加速度，第三个式子是刚体在向量空间的加速度，可见式子(3.21)依然是成立的。
如果刚体$B_1$和刚体$B_2$的速度分别是v${}_1$和v${}_2$，刚体$B_1$相对于刚体$B_2$的速度为v$rel$，那么v${}_2$=v${}_1$+v${}_{rel}$
他们之间的加速度满足如下关系

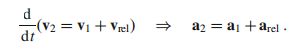
9、空间动量

假设一个刚体的质量为$m$，质心为C，绕过C的直线的转动惯量为$I^{cm}$。如果刚体的空间速度为v${}_c=(w^T{v}_c^T{)}^T$，那么
线动量为$h=m{v}_c$
角动量为$h_C=I^{cm}w$
该刚体绕着某一个点$O$的动量为$h_O=h_C+c\times h$，其中，$c=OC$，即存在如下关系

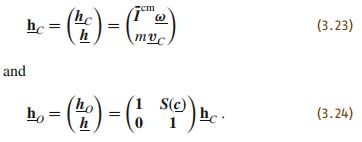
10、空间惯量

刚体的空间动量是其空间惯量和速度的点积h=$Iv$。
用在C处的普吕克坐标来表示为

其中，

上式是对一个质心在C处的刚体的空间惯量的一般表示方式。
但是对于另一点O来说，该刚体的动量表示为

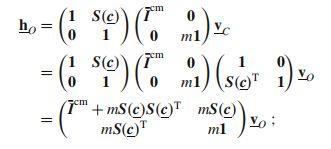
但是该式仍然满足h${}_C$=$I_C{v}_C$的形式，所以可得

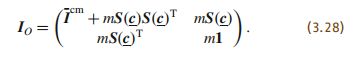
我们继而写成如下形式

其中，

空间惯量矩阵是对称矩阵，也是正定矩阵。要表示空间惯量矩阵需要21个变量，但是刚体的惯量矩阵实际上只有10个参数：质量(1)、质心坐标(3)、$I_O$或者$I^{cm}$的六个独立参数(6)。
对于不同的坐标系$A$和$B$，惯量矩阵之间的变换矩阵为

故而下式也成立。

如果两个刚体的惯量分别是$I_1$和$i_2$，务必注意他俩相对于同一个旋转轴，那么总惯量为$I_{tot}=I_1+I_2$，
其动能为

11、空间运动方程

刚体的受力等于其动量的变化率，故而

再故而