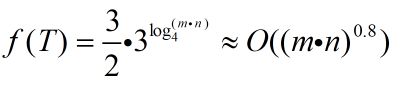LeetCode——240 搜索二维矩阵II

问题描述：

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例:
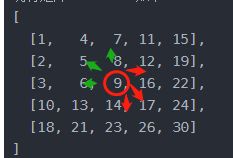
现有矩阵 matrix 如下：
[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]
给定 target = 5，返回 true。

给定 target = 20，返回 false。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/search-a-2d-matrix-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

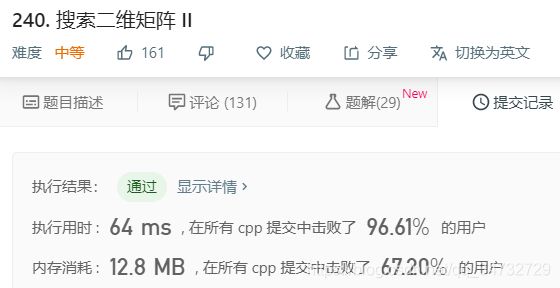
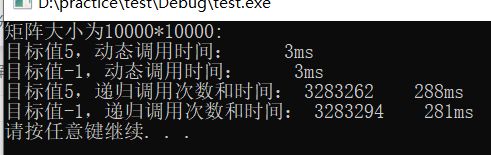
执行结果：

1、递归执行结果：↓

2、更优方案划执行结果：↓

代码描述：

1、递归方式描述：

当取到的中间值，比目标值大或者小时，有三个方向需要进行比较。就像二叉树和三叉树一起的故事。

添加memary，访问过的就不再访问，可以减少递归深度，提高效率。但是，还没有想到办法。

class Solution {
	int m,n;    // 保存矩阵的行数和列数
public:
    bool searchMatrix(vector>& matrix, int target) {
    	if(matrix.size()==0 || matrix[0].size() == 0)
    		return false;
        m = matrix.size(), n =  matrix[0].size();
        int x1 = 0, y1 = 0, x2 = m-1, y2 = n-1;
        bool ans = false;
    	return search(matrix,target,x1,y1,x2,y2,ans);    // 运用递归
    }

    bool search(vector> &matrix, int &target, int x1, int y1, int x2, int y2, bool &ans)    // ans为引用
    {
    	if(ans)
    		return true;
    	if(x1>x2 || y1>y2 || x1<0 || x1>=m || x2>=m || y1<0 || y1>=n || y2>=n)//两头不越界，中间不越界
    		return false;
    	int mx = x1+((x2-x1)>>1);
    	int my = y1+((y2-y1)>>1);
    	if(matrix[mx][my] == target)
        {
            ans = true;
            return ans;
        }
    	if(matrix[mx][my] < target)
    	{
    		search(matrix,target,x1,my+1,mx,y2,ans)
    		    || search(matrix,target,mx+1,y1,x2,my,ans)
    			|| search(matrix,target,mx+1,my+1,x2,y2,ans);//右，下，右下
            return ans;
    	}
    	else
    	{
    		search(matrix,target,x1,my,mx-1,y2,ans)
    			|| search(matrix,target,mx,y1,x2,my-1,ans)
    			|| search(matrix,target,x1,y1,mx-1,my-1,ans);//左，上，左上
            return ans;
    	}
    }
};

2、更优方法描述

将起始位置定位在左下角（右上角也可以），此时，行只能向上，值越来越小，列只能向右，值越来越大，路径沿着一条曲折的线，由左下角，走向右上角。

// 从概率的角度来算，在查找到目标值之前，一定会先处理很多大于、小于的判断。
// 所以，把==的判断放在最后。经过几次程序对比，果然这种方式用时最小。
class Solution {
	int m,n;
public:
    bool searchMatrix(vector>& matrix, int target) {
        if(matrix.size() == 0 || matrix[0].size() == 0) return false;
        int row, col;
        row = matrix.size();
        col = matrix[0].size();
        int x = row-1;
        int y = 0;
        while(x >= 0 && y < col)
        {
            if(matrix[x][y] target)
                --x;
            else
                return true;
        }
        return false;
    }
};

3、两种方法的测试：

调用主函数：

#include
#include
#include
using namespace std;
int main()
{
    vector> test;
	vector temp;
	int NUM = 10001;
	int k = 1;
	for (int i = 1; i < NUM; ++i,++k)
	{
		for (int j = 1; j < NUM; ++j)
		{
			temp.push_back(j+k);
		}
		test.push_back(temp);
		temp.clear();
	}

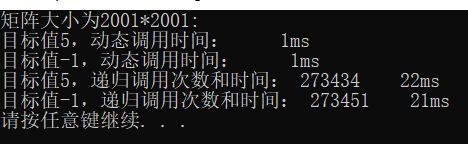
	cout << "矩阵大小为"<

结果对比：

可以看出第二种方案的优越性！！！差距如此之大！

递归的时间复杂度：摘录自：Michael阿明