K-means聚类算法实现鸢尾花聚类
1.实验目的:
了解K-means算法原理并运用K-means算法实现鸢尾花聚类。
2.K-means算法简介
聚类是一个将数据集中在某些方面相似的数据成员进行分类组织的过程,聚类就是一种发现这种内在结构的技术,聚类技术经常被称为无监督学习。k均值聚类是最著名的划分聚类算法,由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k,k由用户指定,k均值算法根据某个距离函数反复把数据分入k个聚类中。
3.K-means算法原理与步骤
K-means算法是典型的基于距离(欧式距离、曼哈顿距离)的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。该算法认为簇是由距离靠近的对象组成的,因此把得到紧凑且独立的簇作为最终目标。
算法步骤:
- 先定义总共有多少个簇类,随机选取K个样本为簇中心。
- 分别计算所有样本到随机选取的K个簇中心的距离。
- 样本离哪个中心近就被分配到哪个簇中心。
- 计算各个中心样本的均值(最简单的方法就是求样本每个点的平均值)作为新的簇心。
- 重复2、3、4直到新的中心和原来的中心基本不变化的时候,算法结束。
算法结束条件:
当每个簇的质心,不再改变时就可以停止k-menas。当循环次数达到事先规定的次数时,停止k-means
原理示意图:
K-means流程图:
欧式距离计算公式:点x= (x_1,x_2,…,x_n)和y= (y_1,y_2,…,y_n)之间的欧式距离为:
曼哈顿距离:点 x= (x_1,x_2,…,x_n)和y= (y_1,y_2,…,y_n)之间的曼哈顿距离为:
簇中心更新公式:在每次迭代过程中,我们需要更新每个簇的中心。假设簇C包含的数据点为x(1),x(2)….x(m),那么簇C的中心可以通过计算簇内所有数据点的均值来得到:
4.鸢尾花数据分析
1)包含3种数据类型,共150条数据
2)包含4个特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度。
5.实验工具
Windows 11、Pycharm.
6.代码实现
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn import datasets
# 直接从sklearn中获取数据集
iris = datasets.load_iris()
X = iris.data[:, :4] # 表示我们取特征空间中的4个维度
print(X.shape)
# 取前两个维度(萼片长度、萼片宽度),绘制数据分布图
plt.scatter(X[:, 0], X[:, 1], c="red", marker='o', label='see')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
def Model(n_clusters):
estimator = KMeans(n_clusters=n_clusters)# 构造聚类器
return estimator
def train(estimator):
estimator.fit(X) # 聚类
# 初始化实例,并开启训练拟合
estimator=Model(3)
train(estimator)
label_pred = estimator.labels_ # 获取聚类标签
# 绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
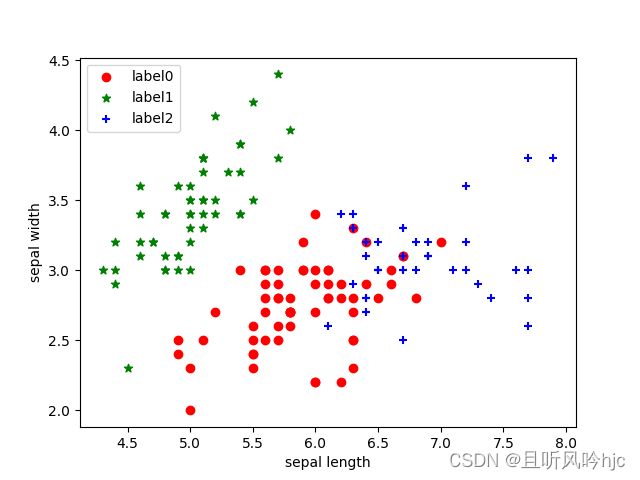
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
# 欧氏距离计算
def distEclud(x, y):
return np.sqrt(np.sum((x - y) ** 2)) # 计算欧氏距离
# 为给定数据集构建一个包含K个随机质心centroids的集合
def randCent(dataSet, k):
m, n = dataSet.shape # m=150,n=4
centroids = np.zeros((k, n)) # 4*4
for i in range(k): # 执行四次
index = int(np.random.uniform(0, m)) # 产生0到150的随机数(在数据集中随机挑一个向量做为质心的初值)
centroids[i, :] = dataSet[index, :] # 把对应行的四个维度传给质心的集合
return centroids
# k均值聚类算法
def KMeans(dataSet, k):
m = np.shape(dataSet)[0] # 行数150
# 第一列存每个样本属于哪一簇(四个簇) 第二列存每个样本的到簇的中心点的误差
clusterAssment = np.mat(np.zeros((m, 2))) # .mat()创建150*2的矩阵
clusterChange = True
# 1.初始化质心centroids
centroids = randCent(dataSet, k) # 4*4
while clusterChange:
# 样本所属簇不再更新时停止迭代
clusterChange = False
# 遍历所有的样本(行数150)
for i in range(m):
minDist = 100000.0
minIndex = -1
# 遍历所有的质心
# 2.找出最近的质心
for j in range(k):
# 计算该样本到4个质心的欧式距离,找到距离最近的那个质心minIndex
distance = distEclud(centroids[j, :], dataSet[i, :])
if distance < minDist:
minDist = distance
minIndex = j
# 3.更新该行样本所属的簇
if clusterAssment[i, 0] != minIndex:
clusterChange = True
clusterAssment[i, :] = minIndex, minDist ** 2
# 4.更新质心
for j in range(k):
# np.nonzero(x)返回值不为零的元素的下标,它的返回值是一个长度为x.ndim(x的轴数)的元组
# 元组的每个元素都是一个整数数组,其值为非零元素的下标在对应轴上的值。
# 矩阵名.A 代表将 矩阵转化为array数组类型
# 这里取矩阵clusterAssment所有行的第一列,转为一个array数组,与j(簇类标签值)比较,返回true or false
# 通过np.nonzero产生一个array,其中是对应簇类所有的点的下标值(x个)
# 再用这些下标值求出dataSet数据集中的对应行,保存为pointsInCluster(x*4)
pointsInCluster = dataSet[np.nonzero(clusterAssment[:, 0].A == j)[0]] # 获取对应簇类所有的点(x*4)
centroids[j, :] = np.mean(pointsInCluster, axis=0) # 求均值,产生新的质心
# axis=0,那么输出是1行4列,求的是pointsInCluster每一列的平均值,即axis是几,那就表明哪一维度被压缩成1
print("cluster complete")
return centroids, clusterAssment
def draw(data, center, assment):
length = len(center)
fig = plt.figure
data1 = data[np.nonzero(assment[:, 0].A == 0)[0]]
data2 = data[np.nonzero(assment[:, 0].A == 1)[0]]
data3 = data[np.nonzero(assment[:, 0].A == 2)[0]]
# 选取前两个维度绘制原始数据的散点图
plt.scatter(data1[:, 0], data1[:, 1], c="red", marker='o', label='label0')
plt.scatter(data2[:, 0], data2[:, 1], c="green", marker='*', label='label1')
plt.scatter(data3[:, 0], data3[:, 1], c="blue", marker='+', label='label2')
# 绘制簇的质心点
for i in range(length):
plt.annotate('center', xy=(center[i, 0], center[i, 1]), xytext= \
(center[i, 0] + 1, center[i, 1] + 1), arrowprops=dict(facecolor='yellow'))
# plt.annotate('center',xy=(center[i,0],center[i,1]),xytext=\
# (center[i,0]+1,center[i,1]+1),arrowprops=dict(facecolor='red'))
plt.show()
# 选取后两个维度绘制原始数据的散点图
plt.scatter(data1[:, 2], data1[:, 3], c="red", marker='o', label='label0')
plt.scatter(data2[:, 2], data2[:, 3], c="green", marker='*', label='label1')
plt.scatter(data3[:, 2], data3[:, 3], c="blue", marker='+', label='label2')
# 绘制簇的质心点
for i in range(length):
plt.annotate('center', xy=(center[i, 2], center[i, 3]), xytext= \
(center[i, 2] + 1, center[i, 3] + 1), arrowprops=dict(facecolor='yellow'))
plt.show()
dataSet = X
k = 3
centroids, clusterAssment = KMeans(dataSet, k)
draw(dataSet, centroids, clusterAssment)
绘图结果展示如下:
7.实验总结
K-means优点:
简单,易于理解和实现;收敛快,一般仅需5-10次迭代即可,高效
缺点:
- 对K值得选取把握不同对结果有很大的不同.
- 对于初始点的选取敏感,不同的随机初始点得到的聚类结果可能完全不同.
- 对于不是凸的数据集比较难收敛.
- 对噪点过于敏感,因为算法是根据基于均值的。
- 结果不一定是全局最优,只能保证局部最优。
- 对球形簇分组效果较好,而对非簇、不同尺寸和不同密度的簇分组效果不好。