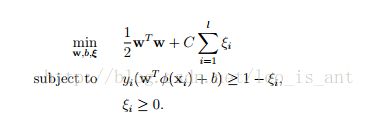初探NO.4—SVM_guide教你直接用支持向量机

写在前面：

  之前学习向量机，理论太多，公式太多。我觉得我这水平不一定能搞明白，更别提写明白。所以我翻译了一片台湾大学的LIBSVM的guide，这个guide介绍了一下SVM，更加注重如何用LIBSVM去让初学者真正体会这个模型。这篇文章的地址是：http://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf

大家可以参考这一篇文章去LIBSVM网站下载其中的代码包和数据集亲自去体验学习，我觉得效果会更好。

PS：英语水平有限，将就的看吧，哈哈~

                          支持向量机的实用初学指南

 

摘要

 

支持向量计算法（SVM）是一种流行的分类技术。然而，这一种技术对于一个初学者而言可能会感到陌生，进而忽略这个算法简单却至关重要的步骤以至于得不到满意的结果。在这个指南中，我们会介绍一种使用算法过程，利用这个过程希望能达到满意的结果。

 

1 介绍

支持向量机（SVMs）是一种优秀的数据分类技术。尽管人们认为支持向量机比神经网路（Neural Networks）要简单，但是初学者利用这一种技术往往一开始也是得不到满意的结果。在这里，我们网上po出一个利用这种技术得到和理解结果的使用之道。

 

请注意，这个使用指南是给SVM的初学者看的，资深SVM研究人员就不需要看了。并且，我们也不能保证你能用这个得到最理想的结果。因此，我们不准备在这一篇文章里解决一些学术上的问题，我们旨在让大家利用SVM得到问题合理的结果。

 

尽管读者没有必要了解SVM背后的复杂理论，但是我们会简要的说一下SVM中重要的知识作为介绍我们使用过程的铺垫。一个分类的任务一般来说分为训练过程和测试过程，每一个训练集合的实例都会包含一个“目标值”（分类的标签）和一些“属性”（特征）。而SVM的目标是创造一个基于训练集模型。这个模型可以当在测试集合只给出“属性”的时候也能计算出实例的“目标值”。

 

一旦给予我们“属性—类别”序列对（训练集）表示成（xi,yi）,i=1,2,3....n, x取值Rn，y取值为±1，这时支持向量机会以下面公式的形式给出问题的最佳解：

                                                    

这里，我们的训练数据向量Xi会被一个函数 ϕ 映射到更高的维度空间。SVM会从高维度空间里找到一个线性的分离超平面将数据以最大的间隔中分离出来。

上述公式中提到的C>0是指一个纠正错误的惩罚因子。

另外呢，有一种叫做核函数的东西，表达式如下图：

                                                               

 

我们可以从介绍有关SVM的书籍里找到4中基本的核函数：

                                       

 

 

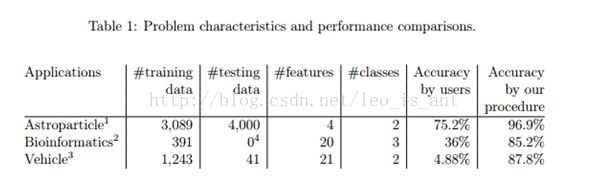
1.1现实中的例子

                            

上面的表格给出了一些应用到了现实世界的案例。这一些案例一开始新手可能得不出很好的分类结果。运用这一个指南，我们可以帮助他们得到更为合理且理想的结果，案例具体解决方案附录A中给出。

关于这一些数据也可以从以下网址获得

www.csie.ntu.edu.tw/~cjlin/papers/guide/data/

 

1.2流程介绍

 

很多的初学者用SVM技术的流程是这样的：

 

1 将数据转换成SVM计算包需的数据形式。

2 随机的运用几个核函数和参数

3 用测试集测试

 

然而我们希望初学者在运用SVM技术的时候采用以下的流程：

 

1 将数据转换成SVM计算包需的数据形式

2 简单的数据缩放

3 考虑用RBF核方法

 

4 用交叉验证去寻求最佳的参数C和γ

5 用步骤4中最佳的参数C和γ去训练整个训练集合

6 测试

我们接下来会讨论这个流程的详细信息。

 

2 数据预处理

2.1 分类的特征

SVM要求每一个数据实例由一组实数向量组成。因此，如果存在一些表示类别的特征，我们首先需要把他们转换成数字形式的数据。我们建议运用m 数字去表示m-类别的属性。只有m类别中的一种是1剩下的把他们归零。与一个例子，假设一个三属性的类别{红，绿，蓝}，这样的分类我们可以把他表示称（0,0,1），（0,1,0）,（1,0,0）.实验显示，属性值如果不是很大计算的代码可能会相对于单一的数字更加稳定。

2.2关于数据缩放

在运用SVM之前对数据进行合理的缩放是必要的

www.faqs.org/faqs/ai-faq/neural-nets

这一篇文章解释了其重要性和运用SVM时的一些考虑要点。对数据进行缩放最大的好处防止不同属性值在过大或者过小的数值域里。另外一个好处是为计算带来便利。因为核函数产生的值一般取决于特征向量的内部值，因为一般说来，线性核函数和多项式核函数对比较大的属性值会造成计算上的困扰。因此，我们推荐线性核函数的值域范围在[-1，+1]，或者[0,1]

  当然我们需要用相同的方法去对训练集合数据集进行同等程度的缩放。比如，我们把训练集的数据从[-10,+10]缩放到了[-1,+1]。如果训练集的属性值域是[-11,+8]我们必须把他们所方法哦[-1.1,+0.8]。在附录B中会介绍一些真实的案例。

3 模型的选择

尽管在前面的章节中只介绍了4种常见的核方法，我们也要决定先选择一种去尝试。之后才能选择最佳的惩罚因子C

3.1 RBF核（径向基函数）

一般说来，RBF核实一种合理的首选。它可以把实例中的特征映射更高层的维度，从而，能解决一些线性核函数解决不了的非线性的问题。其实，当两者惩罚因子作用相同时线性的核是RBF核的特殊的形式。另外sigmoid核和RBF核在一定参数条件下也是类似的。

第二个原因，就是构成的超平面影响着模型选择的复杂程度。例如多项式核就比RBF核的超平面多。

最后，RBF核的计算困难相对小。当层次多的时候RBF核也许是0

不过呢，有一些场景下RBF和也并不是很适合。尤其是当特征数目比较多的时候。有的时候还真得用线性核函数，我们会在附录C中讨论这一些细节。

3.2交叉验证和网格搜索

对于RBF核来说，有两个参数：C和γ。在一开始的时候我们是不知道这个问题的最佳的参数的，但是这个模型还需要这两个参数。所以我们的目标就是找到一组合适的参数（C，γ）

让这个模型去更好的预测位置的信息。请注意，这并不是意味着对于训练集的数据并不是最高的预测正率（拿模型将训练集的数据重新预测一遍）。综上所述，一个常见的策略是将着一些数据分成两组，（虽然都知道标签）我们把一组看成测试集合。那么测试集合的预测正率就更加能反映这个分类器的分类能力。基于这个思想，它的延伸版本就被称作交叉验证。

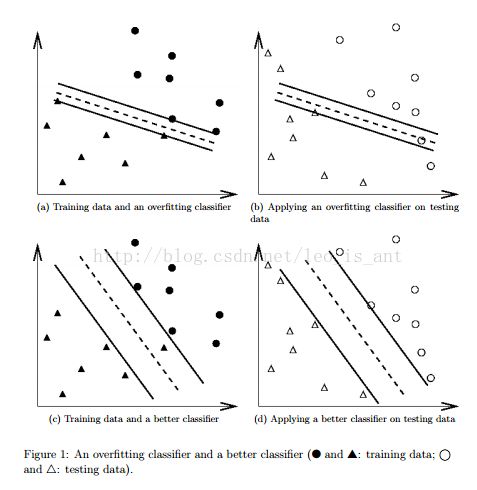
在v折交叉验证中，我们首先把训练集等分成v份。然后我们用一份去作为真正的训练集去验证v-1份训练出来的分类器。这样在整个训练集中的每一个实例都可以被预测一次。所以交叉验证的结果基本上是测试集预测的结果了。

                                              

上面的图就是使用价差验证的原因。防止过拟合。

 

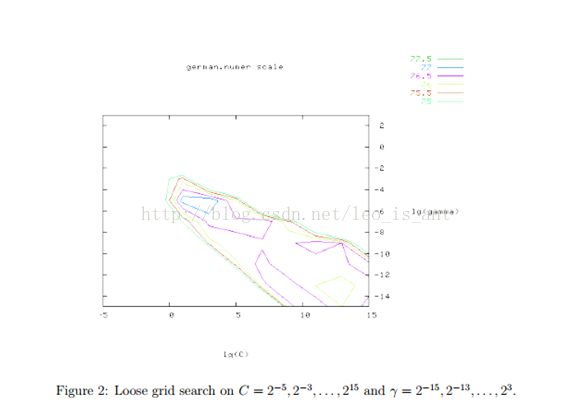
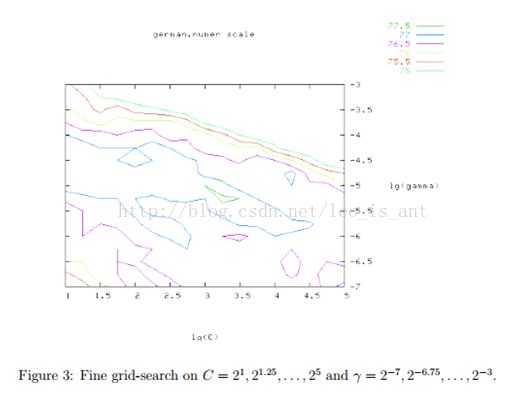
我们推荐在交叉验证中时使用网格搜索找寻参数C和γ。不同的（C，γ）组合将会被尝试然后最佳的交叉验证正确率就会被发现。我们发现指数增长的序列理论上寻找的最好。 比如下图：

                                                                

                                                                                         

                                                                    

  网格搜索看似笨拙却是直截了当。实际上，还有几种先进的方法。但是两个原因使我们选择网格搜索。一是心理上我们懒得用启发式的方法找一个本来就不是很精确地参数。第二，反正就两个参数网格搜索省时省力。而且，这两个参数之间互相独立，也好找。别的先进方法还要详尽细算太麻烦。

  虽然网格搜索很方便，但它也很费时间。所以我们我们建议先粗略地画一个网格。然后从这个网格里找到表现比较良好的一块将它放大。例如下图的例子，在粗略地网隔里最佳的参数是（C，γ）=（）它的交叉验证正确率是77.5%，然后我们在最佳点的附近再找找到的点为（C，γ）=（）。当找到最佳的参数集合的时候，我们训练出来的模型会称为最佳的分类器。

 上述的方法，在千条或者以上数量级时候表现良好。如果数据量大的时候可以进行随机抽取一个子集。然后做一个网格搜索，再用这个延伸到整个训练集合。

 

4额外的讨论

在一些场合下，这一套过程也不是很好。所以像特征选取之类的方法将会被应用。不过这一些问题的范畴已经超过了这个指南。我们通过实验证明这一套路在没有很多特征的时候还是不错的。如果特征数量级达到10^3我们就不得不在使用SVM上面抽取一部分子集了。

 

致谢：略 233333

 

附录 A 一个关于这一套流程的案例

在这一个附录里，我们对比了一下用推荐方法与新手利用SVM的正确率。这三个问题在上面的表格里已经有所体现。每一个问题，我们第一次会直接去训练和测试。之后，我们会po一些经过缩放或者为经过缩放的正确率。这印证了在2.2中讨论的缩放过程。在之后，我们把我们推荐方法的正确率作出记录。最后我们用LIBSVM这一套工具去进行证明。

请注意，下面讨论的参数寻找的工具grid.py会在R-LIBSVM 的接口里。

A.1 天体物理：

未经过任何的处理，用的缺省的参数：

 

PS：上面是LIBSVM工具包的参数命令，这个工具包在LINUX，WIN都能用。而且还给与python matlab等接口，是一个好东西，过后介绍给大家。

 

经过了缩放，仍沿用缺省的参数：

 

用grid.py进行参数&模型选择之后的结果：

 

用Python自动化脚本得出的结果：

 

 

A.2 生物信息学：

未经过任何的处理，用的缺省的参数：

 

经过了缩放，仍沿用缺省的参数：

 

 

用grid.py进行参数&模型选择之后的结果：

 

 

A.3 机动车辆：

未经过任何的处理，用的缺省的参数：

 

经过了缩放，仍沿用缺省的参数：

 

 

用grid.py进行参数&模型选择之后的结果：

 

附录B 缩放数据是经常犯的错误汇总

2.2章节解释了对数据进行缩放的重要性。我们在这一期附录中给出一个具体的交通信号灯的案例。大家可以在下面网址中找到其中的数据集

网址：http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/

如果将训练集合测试集数据分别缩放到[0,1]。正确率会低于70%，如图：

 

 

如果用将他们一起缩放，我们会得到更高的正确率（Leo看了半天没看懂，等着自己试验看一看）：

 

 

在正确的设置之后，在svmguide4.t.scale中的10和特征有以下的最大值：

 

可见，一开始的缩放技术会导致一个错误的结果。

 

附录C 什么时候使用线性核而不是RBF核

如果特征数目太大，也许不需要将特征映射高维。这样，非线性的映射也不会有太多的改善。

用线性核已经很好了，只需要找C就可以了。在讨论了3.1中的线性核之后，我们发现它的表现如果找到合适的参数之后也很不错。

之后，我们将分成三种情况进行讨论：

C.1 实例数目远小于特征数目

在生物信息学中什么情况上属于这一种类型，我们讨论Leukemia的数据。训练集合测试机分别是38条和34条。特征数目是7129个，符合实例数目远小于特征数目。我们将两个文件分开，对比了RBF核和线性核的准确率：

 

感觉，两者差别不大。不过特征数目很大时候，高维映射没有必要。

 

C.2 实例数目&特征数目都很大

这种情况是文件分类所常见的，LIBSVM对这种问题不是很擅长。所幸的是，liblinear对这一类的数据表现的很好我们这用两种工具进行了测试，实例数目和特征数目为20242和47236。结果如图：

 

在交叉验证环节，LIBSVM用了350秒，而liblinear用了3秒。此外，LIBSVM更加消耗内存当用核函数的时候，LIBLINEAR能用快又好的做到分类这一点。

 

而且，请注意读数据占据了大部分时间。

 

 

C.3实例数目远大于特征数目

当特生数目小的时候，一般来说需要进行高维度映射。我们给出一个拥有581k数据实例而只有54个特征的案例，分别运用了线性核和RBF核的结果：

 

 

参考文献：略

= = 终于翻译完了。