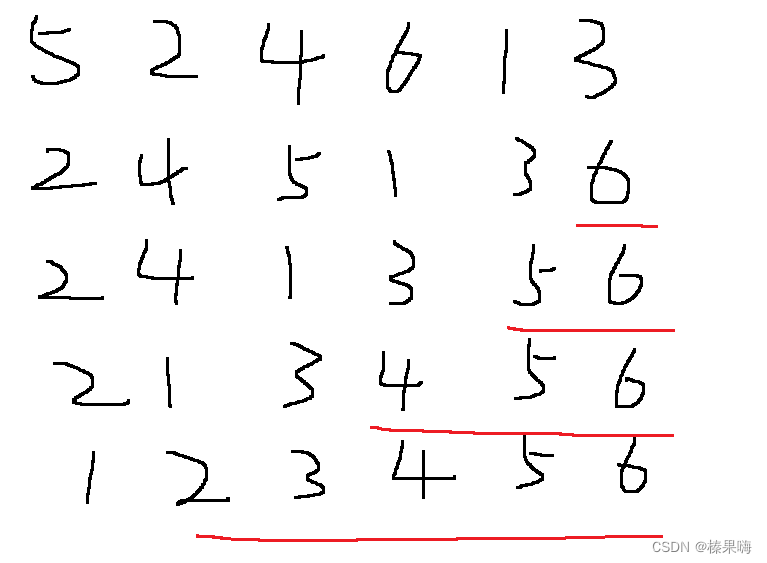六大排序算法：插入、选择、冒泡、快排、希尔、归并

1、插入排序

解析：第一个元素设定为已经排好序，依次选择后续的元素插入到已经排好序的组内进行排序。

图示：

代码：

public static void insertionSort(int[] arr) {
        int n = arr.length;
        
        for (int i = 1; i < n; i++) {
            int key = arr[i];
            int j = i - 1;
            
            // 将比当前元素大的元素向右移动
            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j--;
            }
            
            // 插入当前元素到正确的位置
            arr[j + 1] = key;
        }
    }

时间复杂度：最坏情况下为O(N^2)，此时待排序列为逆序，或者说接近逆序
      最好情况下为O(N)，此时待排序列为升序，或者说接近升序。
空间复杂度：O(1)

2、选择（比较）排序：

解析：每次从待排序列中选出一个最小值，然后放在序列的起始位置，直到全部待排数据排完。

图示：

代码：

public static void selectionSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            int minIndex = i;
            
            // 寻找未排序部分的最小元素的索引
            for (int j = i + 1; j < n; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            
            // 将找到的最小元素与未排序部分的第一个元素交换
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }

时间复杂度：最坏情况：O(N^2)
      最好情况：O(N^2)
空间复杂度：O(1)

3、冒泡排序

解析：左边大于右边交换，一趟排下来最大的在右边

图示：

代码：

public static void bubbleSort(int[] arr) {
        int n = arr.length;
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    // 交换arr[j]和arr[j + 1]
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

时间复杂度：最坏情况：O(N^2)
      最好情况：O(N)
空间复杂度：O(1)

4、快排

解析：

• 1．先从数列中取出一个数作为基准数。
• 2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
• 3．再对左右区间重复第二步，直到各区间只有一个数或者这个区间不存在。

图示：

代码：

public static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            // 划分数组，返回分区点的索引
            int pivotIndex = partition(arr, low, high);
            
            // 递归排序分区左侧和右侧的子数组
            quickSort(arr, low, pivotIndex - 1);
            quickSort(arr, pivotIndex + 1, high);
        }
    }

    public static int partition(int[] arr, int low, int high) {
        int pivot = arr[high]; // 选择最后一个元素作为基准元素
        int i = low - 1;
        
        for (int j = low; j < high; j++) {
            if (arr[j] < pivot) {
                i++;
                // 交换arr[i]和arr[j]
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        
        // 将基准元素放到正确的位置
        int temp = arr[i + 1];
        arr[i + 1] = arr[high];
        arr[high] = temp;
        
        return i + 1;
    }

时间复杂度：O(NlogN)
空间复杂度：O(1)

5、希尔排序

解析：

1.先选定一个小于N的整数gap作为第一增量，然后将所有距离为gap的元素分在同一组，并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量，重复上述操作…
2.当增量的大小减到1时，就相当于整个序列被分到一组，进行一次直接插入排序，排序完成。

图示：

代码：

public static void shellSort(int[] arr) {
        int n = arr.length;
        
        // 初始间隔设为数组长度的一半，然后逐渐缩小间隔
        for (int gap = n / 2; gap > 0; gap /= 2) {
            for (int i = gap; i < n; i++) {
                int temp = arr[i];
                int j;
                for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                    arr[j] = arr[j - gap];
                }
                arr[j] = temp;
            }
        }
    }

时间复杂度平均：O(N)
空间复杂度：O(1)

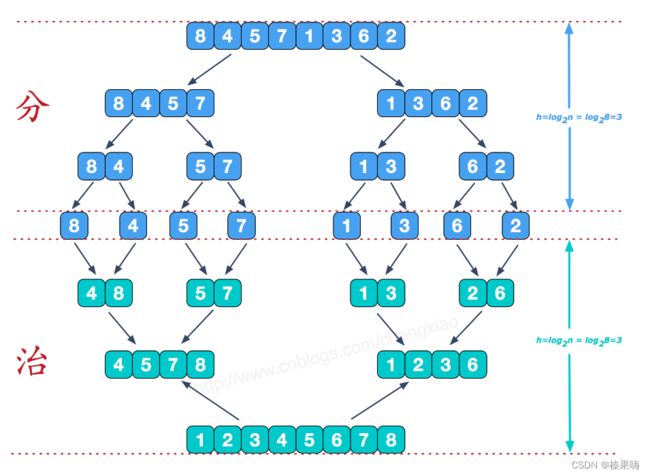
6、归并排序

解析：

1. 将待排序的线性表不断地切分成若干个子表，直到每个子表只包含一个元素，这时，可以认为只包含一个元素的子表是有序表。
2. 将子表两两合并，每合并一次，就会产生一个新的且更长的有序表，重复这一步骤，直到最后只剩下一个子表，这个子表就是排好序的线性表

图示：

代码：

public static void mergeSort(int[] arr) {
        int n = arr.length;
        if (n <= 1) {
            return; // 如果数组长度小于等于1，无需排序
        }
        
        // 将数组分成两个子数组
        int mid = n / 2;
        int[] left = new int[mid];
        int[] right = new int[n - mid];
        
        System.arraycopy(arr, 0, left, 0, mid);
        System.arraycopy(arr, mid, right, 0, n - mid);
        
        // 递归排序左右子数组
        mergeSort(left);
        mergeSort(right);
        
        // 合并两个有序子数组
        merge(arr, left, right);
    }

    public static void merge(int[] arr, int[] left, int[] right) {
        int n1 = left.length;
        int n2 = right.length;
        int i = 0, j = 0, k = 0;
        
        while (i < n1 && j < n2) {
            if (left[i] <= right[j]) {
                arr[k] = left[i];
                i++;
            } else {
                arr[k] = right[j];
                j++;
            }
            k++;
        }
        
        while (i < n1) {
            arr[k] = left[i];
            i++;
            k++;
        }
        
        while (j < n2) {
            arr[k] = right[j];
            j++;
            k++;
        }
    }

时间复杂度平均：O(N)
空间复杂度：O(N)