编译原理——LL1分析程序实验(C#)
LL(1)分析程序实验目的与要求
编制一个能识别由词法分析给出的单词符号序列是否是给定文法的正确句子(程序),输出对输入符号串的分析过程。
实验内容
对于这个实验,核心内容是Process类。该类是一个带有三个参数的构造函数。将初始分析栈,输入的句子,预测分析表作为参数注入该类,调用BeginAnalyze()函数进行分析,同时Process本身属性在函数的循环中发生迭代变化,其自身的属性代表了每一分析步骤的结果,打印即可。
实验步骤
- 主函数内容:先打印出给定文法,预测分析表,然后对用户输入,构造Process类,进行分析。
- 获取推导所用的产生式或匹配:GetProductionRule()
需要调用GetRowIndex(StackTop)和 GetColIndex(Terminal)根据分析栈的栈顶元素与输入字符串首字符来获取预测分析表的内容。 - 反转字符串函数 Reverse(string s):该函数用于将产生式元素逆序入栈
private string Reverse(string s)
{
char[] cs= s.ToCharArray();
Array.Reverse(cs);
return new string(cs);
}
值得一提的是本程序并没有使用Stack数据结构来完成,而是使用了对字符串的操作来代替Stack。
using System;
using System.Collections.Generic;
using static System.Console;
namespace LL1
{
class Program
{
///
/// 文法
///
static List Grammar = new List()
{
"E->TB","B->+TB|ε",
"T->FY","Y->*FY|ε",
"F->i|(E)"
};
///
/// 预测分析表
///
///
static string[,] predictTab =
{
{" ", "i", "+", "*", "(", ")", "#" },
{"E" , "TB", "NULL", "NULL", "TB", "NULL", "NULL" },
{"B" , "NULL", "+TB", "NULL", "NULL", "ε", "ε"},
{"T" , "FY", "NULL", "NULL", "FY", "NULL", "NULL" },
{"Y" , "NULL", "ε", "*FY", "NULL", "ε", "ε" },
{"F" , "i", "NULL", "NULL", "(E)", "NULL", "NULL" }
};
static void Main(string[] args)
{
DisplayG();
DisplayTab();
WriteLine("请输入要分析的串:");
string inputString = ReadLine();
WriteLine("--------------------------------------------------------------------------");
string symbolStack = "#E";
Process process = new Process(symbolStack, inputString, predictTab);
process.BeginAnalyze();
}
///
/// 打印文法列表
///
static void DisplayG()
{
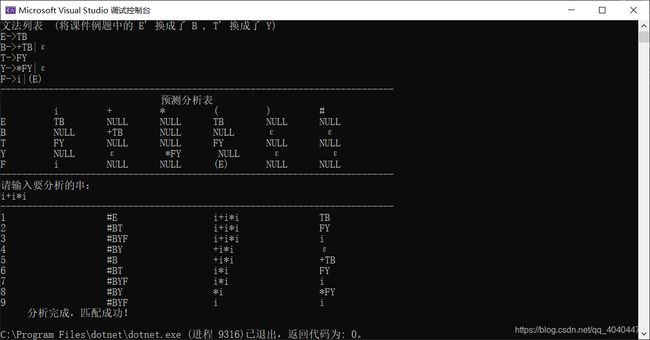
WriteLine("文法列表 (将课件例题中的 E' 换成了 B , T' 换成了 Y)");
foreach (string s in Grammar)
{
WriteLine(s);
}
WriteLine("--------------------------------------------------------------------------");
}
///
/// 打印预测分析表
///
static void DisplayTab()
{
WriteLine("{0,35}", "预测分析表");
for (int i = 0; i < predictTab.GetLength(0); i++)
{
for (int j = 0; j < predictTab.GetLength(1); j++)
{
Write($"{predictTab[i, j],-10}");
}
WriteLine();
}
WriteLine("--------------------------------------------------------------------------");
}
class Process
{
public int index;//步骤
public string symbolStack;//分析栈
public string residueString;//剩余串
public string productionRule;//产生式或匹配
public string[,] predictTab;//预测表
public Process(string symbolStack, string inputString, string[,] predictTab)
{
this.index = 1;
this.symbolStack = symbolStack;
this.residueString = inputString;
this.predictTab = predictTab;
}
//当前输入符号
public string Terminal
{
get
{
return residueString.Substring(0, 1);
}
}
//分析栈栈顶元素
public string StackTop
{
get
{
return symbolStack.Substring(symbolStack.Length - 1, 1);
}
}
//产生式首字符
public string ruleTop
{
get
{
return productionRule.Substring(0,1);
}
}
///
/// LL(1) 分析
///
public void BeginAnalyze()
{
while (true)
{
productionRule = GetProductionRule();
Display();
symbolStack = symbolStack.Substring(0, symbolStack.Length - 1);
if (productionRule== "ε")
{
index++;
continue;
}
if (ruleTop == Terminal)
{
if (residueString.Length == 1)
{
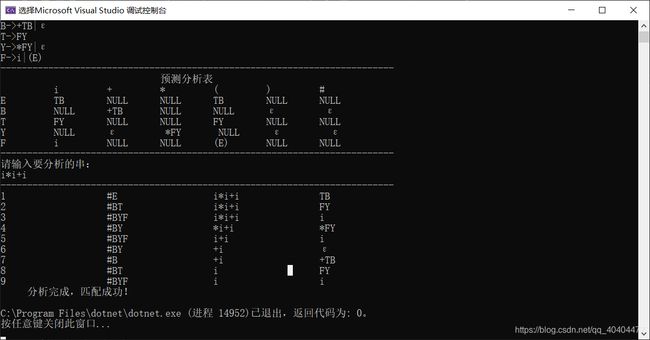
WriteLine(" 分析完成,匹配成功!");
return;
}
else
{
residueString = residueString.Substring(1, residueString.Length-1);
if (productionRule.Length > 1)
{
symbolStack += Reverse(productionRule.Substring(1, productionRule.Length - 1));
}
}
}
else
{
residueString = residueString.Substring(0, residueString.Length);
symbolStack += Reverse(productionRule);
}
index++;
}
}
///
/// 获取推导所用的产生式或匹配
///
///
/// 根据栈顶元素获取行号
///
///
///
/// 根据当前终结符获取列号
///
///
///
/// 反转字符串
///
///
///
/// 打印当前步骤
///
private void Display()
{
WriteLine($"{index,-20}{symbolStack,-20}{residueString,-20}{productionRule,-20}");
}
///
/// 出错处理程序
///
private void Error()
{
WriteLine("!!!!!!!!!!!!!! 语句非法 !!!!!!!!!!!!!!");
Environment.Exit(0);
}
}
}
}