代码随想录算法训练营第五十一天| LeetCode309. 最佳买卖股票时机含冷冻期、LeetCode714. 买卖股票的最佳时机含手续费

一、LeetCode309. 最佳买卖股票时机含冷冻期

        1：题目描述（309. 最佳买卖股票时机含冷冻期）

        给定一个整数数组prices，其中第  prices[i] 表示第 i 天的股票价格 。​

        设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

• 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

        注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

        2：解题思路

        1：确定dp数组以及下标的含义

        dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。

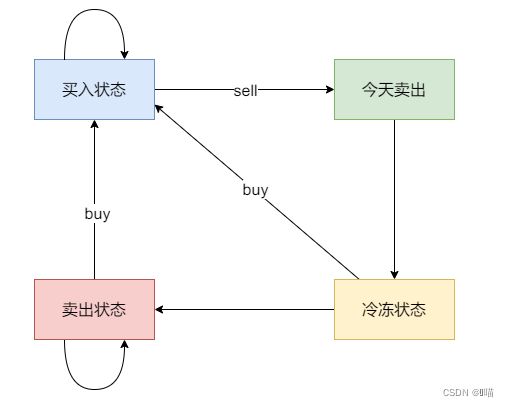
        出现冷冻期之后，状态其实是比较复杂度，例如今天买入股票、今天卖出股票、今天是冷冻期，都是不能操作股票的。 具体可以区分出如下四个状态：

• 状态一：买入股票状态（今天买入股票，或者是之前就买入了股票然后没有操作）
• 卖出股票状态，这里就有两种卖出股票状态
  • 状态二：两天前就卖出了股票，度过了冷冻期，一直没操作，今天保持卖出股票状态
  • 状态三：今天卖出了股票
• 状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

        j的状态为：

• 0：状态一
• 1：状态二
• 2：状态三
• 3：状态四

        注意这里的每一个状态，例如状态一，是买入股票状态并不是说今天已经就买入股票，而是说保存买入股票的状态即：可能是前几天买入的，之后一直没操作，所以保持买入股票的状态。

        2：确定递推公式

        达到买入股票状态（状态一）即：dp[i][0]，有两个具体操作：

• 操作一：前一天就是持有股票状态（状态一），dp[i][0] = dp[i - 1][0]
• 操作二：今天买入了，有两种情况
  • 前一天是冷冻期（状态四），dp[i - 1][3] - prices[i]
  • 前一天是保持卖出股票状态（状态二），dp[i - 1][1] - prices[i]

        所以操作二取最大值，即：max(dp[i - 1][3], dp[i - 1][1]) - prices[i]

        那么dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);

        达到保持卖出股票状态（状态二）即：dp[i][1]，有两个具体操作：

• 操作一：前一天就是状态二
• 操作二：前一天是冷冻期（状态四）

        dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

        达到今天就卖出股票状态（状态三），即：dp[i][2] ，只有一个操作：

• 操作一：昨天一定是买入股票状态（状态一），今天卖出

        即：dp[i][2] = dp[i - 1][0] + prices[i];

        达到冷冻期状态（状态四），即：dp[i][3]，只有一个操作：

• 操作一：昨天卖出了股票（状态三）

        dp[i][3] = dp[i - 1][2];

综上分析，递推代码如下：

dp[i][0] = max(dp[i-1][0], max(dp[i-1][3],dp[i-1][1])-prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][3])
dp[i][2] = dp[i-1][0]+prices[i]
dp[i][3] = dp[i-1][2]

         3：dp数组如何初始化

        这里主要讨论一下第0天如何初始化。

        如果是持有股票状态（状态一）那么：dp[0][0] = -prices[0]，买入股票所剩现金为负数。

        保持卖出股票状态（状态二），第0天没有卖出dp[0][1]初始化为0就行，

        今天卖出了股票（状态三），同样dp[0][2]初始化为0，因为最少收益就是0，绝不会是负数。

        同理dp[0][3]也初始为0。

        4：确定遍历顺序

        从递归公式上可以看出，dp[i] 依赖于 dp[i-1]，所以是从前向后遍历。

代码展示：

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        # 确认dp数组的含义：
        # 分为四个状态：0-买入股票，1-保持卖出股票状态，2-今天卖出股票，3-今天是冷冻期
        # dp[i][j],第i天状态为j，所剩的最多现金为dp[i][j]
        # 确认递推公式
        # 0-买入股票
        # 操作一：前一天就是买入股票的状态，dp[i][0] = dp[i-1][0]
        # 操作二：今天买入股票，两种情况
        # 1：前一天是冷冻期，前一天冷冻期所得最多现金减去今天股票价格就是，所得现金dp[i][0] = dp[i-1][3] - prices[i]
        # 2：前一天是保持卖出状态，前一天保持卖出股票所得最多现金减去今天股票价格就是，所得现金dp[i][0] = dp[i-1][3] - prices[i]
        # 因此：dp[i][0] = max(dp[i-1][0], max(dp[i-1][3],dp[i-1][1])-prices[i])
        # 1-保持卖出股票状态
        # 操作一：前一天就是卖出股票状态，dp[i][1] = dp[i-1][1]
        # 操作二：前一天是冷冻期，dp[i][1] = dp[i-1][3]
        # 因此：dp[i][1] = max(dp[i-1][1], dp[i-1][3])
        # 2-今天卖出股票
        # 前一天就是买入股票的状态，前一天买入股票所得最多现金加上今天股票价格，就是今天卖出股票所得现金，dp[i][2] = dp[i-1][0] + prices[i]
        # 3-今天是冷冻期
        # 前一天就是卖出股票，前一天卖出股票所得最多现金就是今天冷冻期所得最多现金，dp[i][3] = dp[i-1][2]
        # 初始化
        # 根据递推公式，dp[i]都是由dp[i-1]推出来的，所以初始化，dp[0]
        # dp[0][0]=-prices[0],dp[0][1]=0,dp[0][2]=0,dp[o][3]=0
        # 遍历顺序
        # 根据递推公式，dp[i]都是由dp[i-1]推出来的，所以从前向后遍历
        prices_len = len(prices)
        if prices_len == 0:
            return 0
        dp = [[0]*4 for _ in range(prices_len)]
        dp[0][0] = -prices[0]
        for i in range(1, prices_len):
            dp[i][0] = max(dp[i-1][0], max(dp[i-1][3],dp[i-1][1])-prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][3])
            dp[i][2] = dp[i-1][0]+prices[i]
            dp[i][3] = dp[i-1][2]
        # 最后结果是取状态二，状态三，和状态四的最大值，状态四是冷冻期，最后一天如果是冷冻期也可能是最大值。
        return max(dp[-1][1], dp[-1][2], dp[-1][3])

二、LeetCode714. 买卖股票的最佳时机含手续费

        1：题目描述（714. 买卖股票的最佳时机含手续费）

        给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

        你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

        返回获得利润的最大值。

        注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

        2：解题思路

        主要的区别在于：

        卖出股票后，所得最多现金，需要减去手续费

        第i天卖出股票，第i-1买入股票所得最多现金+第i天股票价格再减去手续费就是第i天卖出股票所得最多现金
        dp[i][1] = dp[i-1][0]+prices[i]-fee

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        # 分为两个状态，0-买入股票和1-卖出股票
        # 确认dp数组的含义
        # dp[i][j]，表示第i天状态为j，所得的最多现金是dp[i][j]
        # 确认递推公式
        # 0-买入股票
        # 1：第i-1天已经买入股票，保持现状，dp[i][0] = dp[i-1][0]
        # 2：第i天买入股票，第i-1天卖出股票所得最多现金减去第i天的股票价格就是第i天买入股票所得最多现金
        # dp[i][0] = dp[i-1][1]-prices[i]
        # 因此：dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i])
        # 1-卖出股票
        # 1：第i-1天就卖出股票，保持现状，dp[i][1] = dp[i-1][1]
        # 2：第i天卖出股票，第i-1买入股票所得最多现金+第i天股票价格再减去手续费就是第i天卖出股票所得最多现金
        # dp[i][1] = dp[i-1][0]+prices[i]-fee
        # 因此：dp[i][1] = max(dp[i-1][1], dp[i-1][0]+prices[i]-fee)
        # 初始化
        # 由递推公式得出，dp[i]由dp[i-1]推出的，所以初始化dp[0]
        # dp[0][0] = -prices[0]，dp[0][1] = 0
        # 遍历顺序
        # 由递推公式得出，dp[i]由dp[i-1]推出的，所以从前往后进行遍历
        prices_len = len(prices)
        if prices_len == 0:
            return 0
        dp = [[0]*2 for _ in range(prices_len)]
        dp[0][0] = -prices[0]
        for i in range(1, prices_len):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][0]+prices[i]-fee)
        # 最后返回最后一天卖出股票所得现金，就是获得的最大利润
        return dp[-1][1]