Flutter CustomPaint 绘制声音波动曲线

目标效果：

Part 1

曲线绘制的实现

无论原生，Flutter还是前端， 曲线的绘制在不同平台实现都大同小异。 通过确定不同点的位置坐标（x1, y1）（x2,y2）... ，然后用过贝塞尔曲线或者 系统方法拟合两点之间的曲线，最后把 曲线path给到画布绘制，这样曲线就出来了。

小插曲

• 最终效果是 开始和末尾振幅为0 向中间位置递增的曲线。
• 我们从基础开始，我们先画条振幅相同的曲线，并波动。
• 写代码要循循渐进，一步步的来。。。

这简单啊~

• 画条两倍容器view宽的波纹曲线
• 重复从左到右滑动，视觉效果就是曲线波动的效果

搞定后，设计说上面这个是当时偷懒给错了图，当时内心的想法

平复下情绪，那我们就把 振幅相同 和 振幅不同 的曲线都分享下。

绘制振幅相同的曲线

class VoiceWavePainter extends CustomPainter {
  @override
  void paint(Canvas canvas, Size size) {
    Paint paint = Paint()
      ..color = Colors.red
      ..style = PaintingStyle.stroke
      ..strokeWidth = 2;
    Path path = Path();
    // 
    path.quadraticBezierTo(50, -80, 100, 0);
    path.quadraticBezierTo(150, 80, 200, 0);

    canvas.drawPath(path, paint);
  }

  @override
  bool shouldRepaint(VoiceWavePainter oldDelegate) => false;
}

path.quadraticBezierTo 定义P1和P2位置 一个类似正弦的曲线绘制完成，P0是路径起始点。

path.quadraticBezierTo(50, -80, 100, 0);
    P0（0，0）
    P1 (50,-80)
    p2 (100,0)
    path.quadraticBezierTo(150, 80, 200, 0);
    P0（100，0）
    P1 (150,80)
    p2 (200,0)

以此类推，就出现需要的类正弦曲线。

振幅相同的曲线的波动

原理已经说过不再重复，图示更直观, 重复的左滑动， 矩形框左右两侧波形 左滑的开始和结束时完全一样的，视觉效果就产生曲线一直波动的效果。

最终实现

  @override
  void paint(Canvas canvas, Size size) {
    int waveNum = 4;
    double waveWidth = this.painterWidth / waveNum;
    
    canvas.clipRect((Rect.fromCenter(
        center: Offset(0, size.height / 2),
        width: painterWidth * 2,
        height: 120)));
    canvas.translate(0, size.height / 2);
    Paint paint = Paint()
      ..color = Colors.red
      ..style = PaintingStyle.stroke
      ..strokeWidth = 2;

    Path path = Path();
   
    for (var i = 0; i < waveNum * 2; i++) {
      path.quadraticBezierTo(waveWidth / 2 + waveWidth * i,
          waveHeight * (i.isOdd ? 1 : -1), waveWidth * (i + 1), 0);
    }
    canvas.translate(-painterWidth * repaint.value, 0);
    canvas.drawPath(path, paint);
  }
}

  class _VoiceWaveState extends State
    with SingleTickerProviderStateMixin {
  AnimationController _waveController;
  @override
  void initState() {
    _waveController =
        AnimationController(vsync: this, duration: Duration(seconds: 1))..repeat();
  }

  @override
  void dispose() {
    _waveController.dispose();
    super.dispose();
  }

• 定义 AnimationController 并传入 自定义的 CustomPainter。
• painterWidth 曲线的长度 waveNum 可见波动的个数。
• waveWidth = this.painterWidth / waveNum，waveWidth 是半个波长的长度。

    for (var i = 0; i < waveNum * 2; i++) {
       path.quadraticBezierTo(waveWidth / 2 + waveWidth * i,
          waveHeight * (i.isOdd ? 1 : -1), waveWidth * (i + 1), 0);
    }

• 循环定义点位的位置，假如要看到4个上下波峰长的曲线，我们需要绘制8的上下波峰的曲线，共16 个坐标点，简化后通过循环确定点的位置。
• 通过 canvas.translate(-painterWidth * repaint.value, 0) 实现canvas的重复移动。

总结

• 优点
  • 能够快速实现曲线波动的效果。
• 缺点
  • 波动个数必须是半个的正弦周期的整数倍，奇数的话 重复动画的开始和奇数的点y值正好相反，无所出现连贯的动效。
  • 无法使用渐变色效果。

---

Part 2

效果图所示曲线的实现原理以及代码实现过程是什么呢？

首先要对需求有着确切的分析后，明确需求的大概实现思路，那么需求就已经实现了一半。

分析

1. 明确动画是不是有规律的？

• 确定是一个 振幅有规律递增递减的正弦函数，如果无规律则无法实现。

2. 曲线的函数表达式是什么？

• 正弦函数的表达式 y=A sin(ωx+φ)， 振幅有规律递增递减的正弦函数是什么？需要明确函数表达式。

思路

1. 通过确定曲线函数表达式，绘制递增递减的静态曲线

2. 通过改变静态曲线的函数某些参数，实现曲线的波动

工欲善其事，必先利其器

推荐个工具,不仅更直观函数的图像表达，还可以设置参数调试动画效果

• Desmos | 图形计算器

 实在是居家旅行、杀 * 灭 *、必备良药

曲线的表达式

可惜数学都留在了校园，但曲线的形状感觉在哪里见到过，感觉像是信号与系统里的载波信号，经过上述工具的推算，最终表达式其实是两个正弦函数的乘积。

• f(x) = A * sin(b * x) * sin(c * x)

曲线的绘制

void paint(Canvas canvas, Size size) {
    // 获取采样点
    initPoints();
    // 画笔
    Paint paint = Paint()
      ..color = Colors.red
      ..strokeWidth = 2
      ..style = PaintingStyle.stroke;
    // 路径
    Path path = Path();
    canvas.translate(0, size.height / 2);
    // 通过点确定曲线路径
    for (var i = 1; i < xAliax.length - 1; i++) {
      double x1 = xAliax[i];
      double y1 = funcSquaredSinx(x1);
      double x2 = (xAliax[i] + xAliax[i + 1]) / 2;
      double y2 = (y1 + funcSquaredSinx(xAliax[i + 1])) / 2;
      path.quadraticBezierTo(x1, y1, x2, y2);
    }
    // 画布绘制
    canvas.drawPath(path, paint);
  }

   //曲线函数表达式
   double funcSquaredSinx(double x) {
    double p = 30 * sin(3 * pi * x / 400) * sin(x * pi / 400);
    return p;
  }

• 采样点 [x1,x2,x3,....] 经过funcSquaredSinx 计算出y值。
• 通过path.quadraticBezierTo(x1, y1, x2, y2) 采样点相连接，最终绘制出曲线。

曲线波动效果

 首先需要思考一个问题，我们如何让曲线实现波动效果？

- 振幅相同曲线通过canvas移动 实现曲线波动，在这里肯定不适应

• 我们是采样点链接绘制路径，只有改变采样点的y值，需要从函数funcSquaredSinx入手。

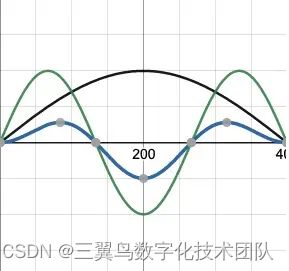
正弦函数 y=A sin(ωx+φ) 的平移 是由φ决定, 所以只需要控制funcSquaredSinx 中 sin(3 * pi * x / 400 + φ) 中 φ 便可以可以平移曲线。用工具演示如下：

曲线波动的代码实现

只需要我们传入 Animation *repaint 更改函数表达式

   Tween(begin: 0.0, end: 1.0).animate(_controller)

   //曲线函数表达式
   double funcSquaredSinx(double x) {
    double p = 
    30 * sin(3 * pi * x / 400 - 100 * repaint.value) * sin(x * pi / 400);
    return p;

  }

• 动画不断重绘，采样点的y值不断改变，路径不断改变，每一帧的路径渐变，产生动画
• Canvas 可以绘制多条曲线，三条曲线初始相位不同和振幅不同，自定义每条线的粗细和颜色，便产生了首图的效果

 三条曲线并加入渐进色

 三条曲线并加入渐进色

 总结

• 优点
  • 任意曲线动效都能实现
  • 支持渐变色
• 缺点
  • 不断重绘path，相对canvas移动更消耗性能，但在接受范围之内

两种曲线的绘制方式

1. 固定点的位置，固定路径绘制，移动画板canvas
2. 刷新点的位置，不断重绘路径，生成动画

公式总结：