【C++】AVL树插入过程详解
学习导航
-
-
- (1)AVL树的性质
- (2)AVL树的结点定义
- (3)AVL树的插入
-
- 1. 基本步骤
- 2. 插入新结点
- 3. 更新平衡因子
- (4)AVL树的旋转
-
- 1.基本认识
- 2.左单旋
- 3.右单旋
- 4.左右双旋
- 5.右左双旋
-
(1)AVL树的性质
二叉搜索树虽然可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家 G.M.Adelson-Velskii 和 E.M.Landis 在1962年发明了一种解决上述问题的方法:
当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度 。
总而言之,AVL树具有如下的性质:
- 它的所有子树都是AVL树
- 左右子树之间的高度差(平衡因子)的绝对值不能超过1
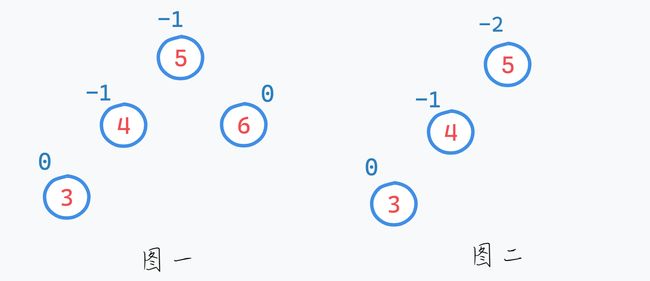
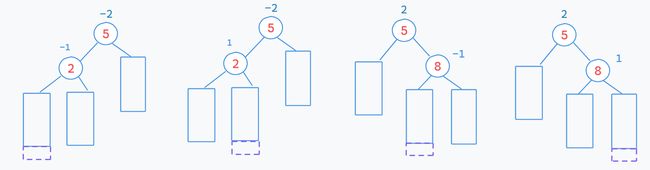
我们定义 平衡因子 = 右子树高度 - 左子树高度。各个结点的平衡因子大小如上,根据 AVL 树的定义易得,图一为 AVL 树, 图二不是AVL树。
(2)AVL树的结点定义
我们模拟实现KV模型的AVL树,K模型的同理易得
template<class K, class V> struct AVLTreeNode { AVLTreeNode<K, V>* _left; AVLTreeNode<K, V>* _right; AVLTreeNode<K, V>* _parent; // 键值对 pair<K, V> _kv; // 平衡因子:balance factor int _bf; AVLTreeNode(const pair<K, V>& kv) :_kv(kv) ,_left(nullptr) ,_right(nullptr) ,_parent(nullptr) ,_bf(0) {} };[注意]:AVL树并没有要求一定要实现平衡因子,在操作时也可以通过高度函数来计算,只不过相对麻烦。
(3)AVL树的插入
1. 基本步骤
AVL树的插入过程可以大致分为以下三步:
- 按照二叉搜索树的的规则插入新节点
- 更新相关结点的平衡因子
- 对于不满足平衡因子小于2的子树进行旋转
接下来就这三个步骤分别加以叙述
2. 插入新结点
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也是二叉搜索树的一种,其插入过程与二叉搜索树别无二致:
- 若待插入结点的k值小于当前父结点,则与左孩子继续比较
- 若待插入结点的k值大于当前父节点,则与右孩子继续比较
- 若待插入结点的k值与父节点相同,则插入失败,返回false,因为键(K)不允许重复
重复上述过程直至为空,在空节点位置处进行插入。参考代码如下:
template<class K, class V> class AVLTree { public: typedef AVLTreeNode<K, V> Node; bool Insert(const pair<K, V>& kv) { // (1) 按照二叉搜索树的方式插入新结点 Node* newnode = new Node (kv); // _root为空时直接插入即可,不需要调节平衡因子 if (_root == nullptr) { _root = newnode; return true; } Node* parent = nullptr; Node* cur = _root; while (cur) { parent = cur; if (cur->_kv.first > kv.first) { cur = cur->_left; } else if (cur->_kv.first < kv.first) { cur = cur->_right; } else { return false; // 键相同的情况 } } if (parent->_kv.first > kv.first) { parent->_left = newnode; newnode->_parent = parent; } else { parent->_right = newnode; newnode->_parent = parent; } cur = newnode; // (2) 调节平衡因子 // …… 代码见下 return true; } private: Node* _root = nullptr; };
3. 更新平衡因子
因为平衡因子 = 右子树高度 - 左子树高度,所以我们容易建立以下认识:
- 在右子树插入结点,父节点平衡因子一定会
+ 1- 在左子树插入结点,父节点平衡因子一定会
- 1- 新插入的结点可能会影响父节点的平衡因子,但一定不会影响兄弟结点的平衡因子
- 父节点平衡因子的变化可能会进一步引起祖父结点平衡因子的变化
基于上面的认识,很显然,当我们插入一个新结点时,父节点平衡因子的变化是确定的,有以下三种可能:(平衡因子都指的是父节点的)
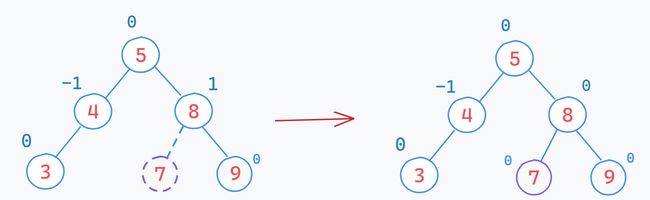
【情况一】:平衡因子变为
0【处理】:更新结束
【分析】:原平衡因子只可能为
-1或1,插入新结点后变为0,说明对于祖父结点来说,其子树的高度没有发生变化,因而不需要向上调整。【案例】:
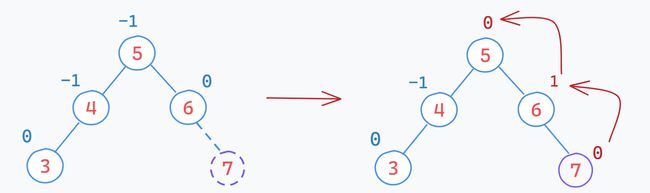
【情况二】:平衡因子变为
-1 或 1【处理】:继续往上更新
【分析】:原平衡因子只可能为
0,插入新结点后变为-1 或 1,说明子树的高度变了,会影响祖父结点的平衡因子,所以需要往上更新。【案例】:
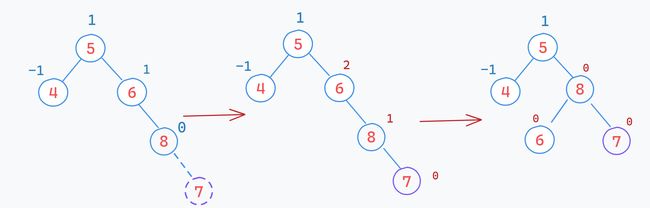
【情况三】:平衡因子变为
2 或 -2【处理】:旋转(具体操作见下文分解)
【分析】:不满足AVL树的特性,需要通过旋转保证平衡因子不超过1
【案例】:
参考代码如下:
template<class K, class V> class AVLTree { public: typedef AVLTreeNode<K, V> Node; bool Insert(const pair<K, V>& kv) { Node* newnode = new Node (kv); // (1) 按照二叉搜索树的方式插入新结点 // …… 代码见上 // (2) 调节平衡因子 cur = newnode; while (parent) { if (cur == parent->_right) { parent->_bf++; } else { parent->_bf--; } // 检测是否需要继续调节 // 说明子树没有变长,不会影响父节点 if (parent->_bf == 0) { break; } // 说明子树变长,继续调整 else if (abs(parent->_bf) == 1) { parent = parent->_parent; cur = cur->_parent; } // 不平衡,则需要旋转处理 else if (abs(parent->_bf) == 2) { // 不理解没关系,见下面分解 if (parent->_bf == -2 && cur->_bf == -1) { RotateR(parent); } else if (parent->_bf == 2 && cur->_bf == 1) { RotateL(parent); } else if (parent->_bf == -2 && cur->_bf == 1) { RotateLR(parent); } else if (parent->_bf == 2 && cur->_bf == -1) { RotateRL(parent); } break; } else // 说明在插入前就出现了问题 { assert(false); } } return true; } private: Node* _root = nullptr; };
(4)AVL树的旋转
1.基本认识
关于旋转,我们首先要建立起如下的基本认识:
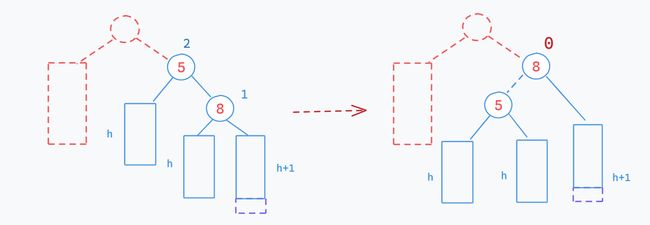
2.左单旋
[适用情况]:
parent→_bf = 2 ; subR→_bf = 1[如何旋转]:
所谓左旋就是以sub结点为轴,将parent结点向左旋转,以此来降低子树高度,从而维持平衡
- 需要调整pparent,parent、subR、subRL之间的链接关系
- 旋转后更新平衡因子
[链接注意点]:
- 如果子树的高度 h = 0,那么subRL即为空树。因此你不需要使
subRL->parent = parent,因为你不能解引用空指针- 如果parent为根节点,那么pparent为空指针,因此你不能解引用空指针pparent,所以直接使得
_root = subR即可
[平衡因子的更新]:
- 旋转只会影响parent和subR子树的高度,所以我们只需要调整这两个结点的平衡因子即可
- 从图中不难发现,旋转和parent和subR的平衡因子都变成0
如果上面的讲解不太理解,就再看看代码吧:
template<class K, class V> class AVLTree { public: typedef AVLTreeNode<K, V> Node; private: void RotateL(Node* parent) { Node* pparent = parent->_parent; Node* subR = parent->_right; Node* subRL = subR->_left; parent->_right = subRL; // 注意点1:小心subRL为空的情况 if (subRL) { subRL->_parent = parent; } parent->_parent = subR; subR->_left = parent; // 注意点2:小心parent的头结点为空的情况 if (parent == _root) { _root = subR; subR->_parent = nullptr; } else { subR->_parent = pparent; // 判断是插在pparent的左子树还是右子树 if (parent == pparent->_left) { pparent->_left = subR; } else { pparent->_right = subR; } } // 平衡因子的调节 parent->_bf = 0; subR->_bf = 0; } }
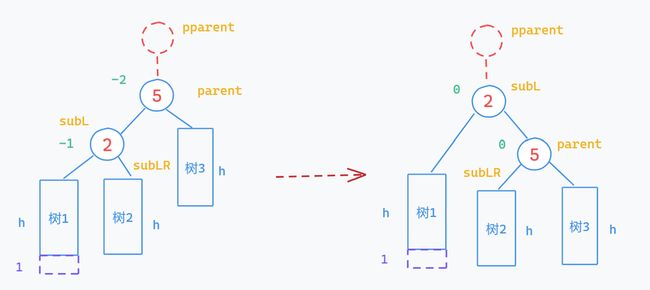
3.右单旋
[适用情况]:
parent→_bf = -2 subR→_bf = -1[如何旋转]:
所谓右旋就是以sub结点为轴,将parent结点向左旋转,以此来降低子树高度,从而维持平衡处理过程与注意点与左旋转基本相同,这里直接呈现参考代码:
template<class K, class V> class AVLTree { public: typedef AVLTreeNode<K, V> Node; private: void RotateR(Node* parent) { Node* pparent = parent->_parent; Node* subL = parent->_left; Node* subLR = subL->_right; parent->_left = subLR; // 注意点1;小心subLR为空树 if (subLR) { subLR->_parent = parent; } subL->_right = parent; parent->_parent = subL; // 注意点2:小心parent的头结点为空的情况 if (parent == _root) { _root = subL; subL->_parent = nullptr; } else { subL->_parent = pparent; if (parent == pparent->_left) { pparent->_left = subL; } else { pparent->_right = subL; } } // 平衡因子的调节 parent->_bf = 0; subL->_bf = 0; } }
4.左右双旋
[适用情况]:
parent→_bf = -2 subR→_bf = 1[如何旋转]:顾名思义,就是先左旋再右旋
- 左右双旋的实现很简单,直接调用我们已经实现的
RotateL()和RotateR()函数即可- 唯一需要做的是更新两次旋转后的平衡因子
[平衡因子的更新]:
平衡因子的更新有三种情况,可以用旋转前subLR的平衡因子bf做区分
新插入结点在树2后,即bf = -1(如上图所示)
subL->_bf = 0; subLR->_bf = 0; parent->_bf = 1;新插入的结点在树3后,即bf = 1
subL->_bf = -1; subLR->_bf = 0; parent->_bf = 0;当 h = 0时,如下图所示
subL->_bf = 0; subLR->_bf = 0; parent->_bf = 0;
参考代码如下:
void RotateLR(Node* parent) { Node* subL = parent->_left; Node* subLR = subL->_right; int bf = subLR->_bf; // 先左旋,再右旋 RotateL(subL); RotateR(parent); // 重新调节平衡因子 if (bf == 0) { subL->_bf = 0; subLR->_bf = 0; parent->_bf = 0; } else if (bf == 1) { subL->_bf = -1; subLR->_bf = 0; parent->_bf = 0; } else if (bf == -1) { subL->_bf = 0; subLR->_bf = 0; parent->_bf = 1; } else // 说明之前就出现错误 { assert(false); } }
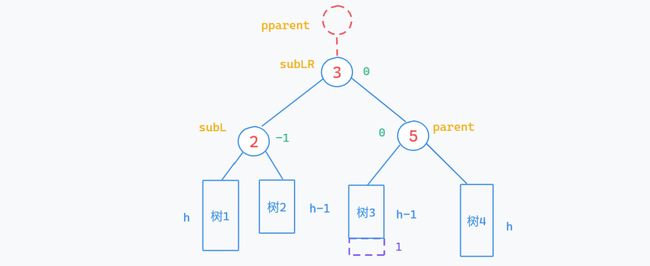
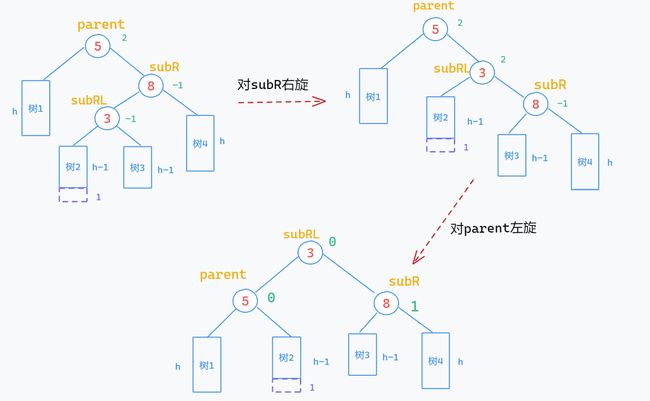
5.右左双旋
[适用情况]:
parent→_bf = 2 subR→_bf = -1[如何旋转]:顾名思义,就是先右旋再左旋
[平衡因子的更新]:
平衡因子的更新有三种情况,可以用旋转前subLR的平衡因子bf做区分:
新插入结点在树2后,即 bf = -1(如上图所示)
subR->_bf = 1; subRL->_bf = 0; parent->_bf = 0;新插入结点在树3后,即 bf = 1
subL->_bf = 1; subRL->_bf = 0; parent->_bf = -1;h = 0时,如下图所示
subR->_bf = 0; subRL->_bf = 0; parent->_bf = 0;参考代码:
void RotateRL(Node* parent) { Node* subR = parent->_right; Node* subRL = subR->_left; int bf = subRL->_bf; RotateR(subR); RotateL(parent); // 重新调节平衡因子 if (bf == 0) { subR->_bf = 0; subRL->_bf = 0; parent->_bf = 0; } else if (bf == 1) { subR->_bf = 0; subRL->_bf = 0; parent->_bf = -1; } else if (bf == -1) { subR->_bf = -1; subRL->_bf = 0; parent->_bf = 0; } else { assert(false); } }