【软件测试】自动化测试战零基础教程——Python自动化从入门到实战(完结)

整理不易，希望对各位学习软件测试能带来帮助

第十章 行为驱动开发 BDD 框架 lettuce 入门

看到 TDD/BDD 一定会感觉高端大气上档次，不是我们普通吊民玩的，最的近在一直在摸索自动化测试。也想体验并引入 BDD 低调奢华的内涵。于是，在网络上搜索资料；话说这玩艺儿真的不太好理解，尤其对于没有丰富编程的经验的同学。
学习 BDD ruby 的 cucumber 是个不错的选择，但我是 python 流的，自然找了来它的兄弟 lettuce ，从官方版本（v0.1rc11）来看确实够年轻的，不过由 ruby 的 cucumber 在前面开路，lettuce 应该会发展的很顺利。
lettuce 除了官方文档外，几乎找不到其它资料，为了理解 lettuce ，我们不妨多去看看 cucumber的资料。
lettuce 是一个非常有用的和迷人的 BDD（行为驱动开发）工具。Python 项目的自动化测试，它可以执行纯文本的功能描述，就像 ruby 语言的 cucumber。
lettuce，使开发和测试过程变得很容易，可扩展性，可读性和-什么是最好的-它允许我们用自然语言去描述个一个系统的行为，你不能想象这些描述可以自动测试你的系统。

第一节、安装与例子

lettuce 官方网址：http://lettuce.it/

安装

请确认你已经安装了 python 以及 pip 安装包管理工具。
不管是 windows 还是 linux 环境，进入 pip 目录，只需下面一个命令就可以安装 lettuce .
user@machine:~$ [sudo] pip install lettuce
安装好 lettuce 后，如果在终端直接执行 lettuce 命令，得到以下输出：

哎呀！不能发现 features ，lettuce 期望在当前目录下创建 features 子目录

例子（阶乘）

下面就通过官网的例子来领略 lettuce 的风骚。
什么阶乘？
0！=1
1！=1
2！=2×1=2
3！=3×2×1=6
…
10!=10×9×8×7×6×5×4×3×2×1=3628800
…
下面是用 python 语言的两种阶乘实现：

#coding=utf-8
#循环实现
def f(n):
c = 1
for i in range(n):
i=i+1
c=c*i
return c
#递归实现
def f2(n):
if n > 1:
return n*f2(n-1)
else:
return 1
#调用方法
print f(10)
print f2(10)

OK！介于我们理解上面阶乘的基础上，来看看 BDD 是如何实现的。

第二节、lettuce 解析

创建以下目录结构：
…/tests/features/zero.feature
/steps.py
现在我们来编写 zero.feature 文件的内容

Feature: Compute factorial
In order to play with Lettuce
As beginners
We'll implement factorial
Scenario: Factorial of 0
Given I have the number 0
When I compute its factorial
Then I see the number 1

我这里对上面的内容做个翻译：

功能： 计算阶乘
为了使用 lettuce
作为初学者
我们将实现阶乘
场景： 0的阶乘
假定我有数字0
当我计算它的阶乘
然后，我看到了1

是不是很自然的描述？！第一段功能介绍，我要实现什么功能；第二段场景，也可以看做是一条测试用例，当我输入什么数据时，程序应该返回给我什么数据。

虽然是自然语言，但还是有语法规则的，不然一千个人有一千中描述，程序以什么样的规则去匹配呢？

其实它的语法规则非常简单就几个关键字，记住他们的含义及作用即可。

---

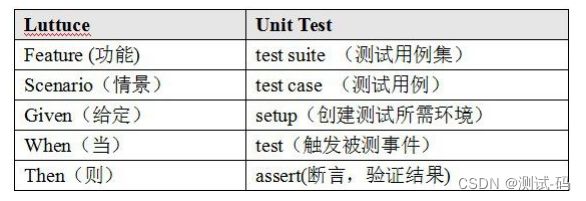
• Feature（功能）
• Scenario（情景）
• Given（给定）
• And（和）
• When（当）
• Then（则）

---

他们的含义与原有自动化测试框架的概念相似，类比如下：

关于 feature 文件的作用，执行以及语法规则将在下一节中详细介绍，这一节主要先来体验 luttuce的风骚。
有了上面 zero.feature 文件的行为做指导，下面打开 steps.py 文件来编写我们的程序。

from lettuce import *
@step('I have the number (\d+)')
def have_the_number(step, number):
world.number = int(number)
@step('I compute its factorial')
def compute_its_fatorial(step):
world.number = factorial(world.number)
@step('I see the number (\d+)')
def check_number(step, expected):
expected = int(expected)
assert world.number == expected, \
"Got %d" % world.number
def factorial(number):
number = int(number)
if (number == 0) or (number == 1):
return 1
else:
return number

咋一看怎么跟我上面实现阶乘的代码相差甚远呀！不知道你和你的小伙伴有没有惊呆！？好吧，以我拙劣的 python 语言水平试着来分析一下，这是啥？这是啥？这又是啥？

from lettuce import *
引入 lettuce 下面的所有包

@step(‘I have the number (\d+)’)
@step 字面意思是步骤
I have the number (\d+) 对应的就是 zero.feature 文件中的第六句：Given I have the number 0
(\d+) 是一个正则表达式，\d 表示匹配一个数字，+ 表示匹配的数字至少有一个或多个。关于这个可以参考其他 python 正则表达式的资料。

第一步：

@step('I have the number (\d+)')
def have_the_number(step, number):
world.number = int(number)

定义一个方法 have_the_number，把假设的输入（0）转换成整型放入 world.number 中。

第二步：

@step('I compute its factorial')
def compute_its_fatorial(step):
world.number = factorial(world.number)

把 have_the_number 方法中 world.number 的变量值（0）放入 factorial() 方法中，并把结果返再赋值给 world.number 变量。
I compute its factorial 对应的就是 zero.feature 文件中的第七句：When I compute its factorial

第三步：

def factorial(number):
number = int(number)
if (number == 0) or (number == 1):
return 1
else:
return number

这个是 factorial()方法被调用时的处理过程，对参数的内容转换成整数，判断如果等于0或1的话就直接
返回1，否则返回具体的数。（处理结果给了第三步的 world.number）

第四步：

@step('I see the number (\d+)')
def check_number(step, expected):
expected = int(expected)
assert world.number == expected, \
"Got %d" % world.number

expected 获取的是 zero.feature 文件中预期结果， 与第三步处理的实际结果（world.number）进行比较；assert 函数进行断言结果是否正确。
I see the number (\d+)对应的就是 zero.feature 文件中的第八句：Then I see the number 1

运行
切换到 tests 目录下，运行 lettuce 命令：
fnngj@fnngj-H24X:~/python/lettuce/tests$ lettuce
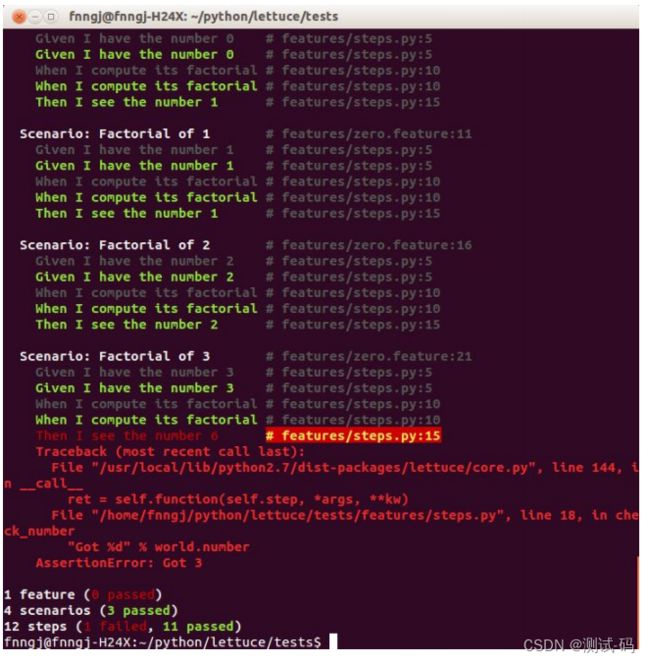
运行结果如下：

运行结果很清晰，首先是 zero.feature 文件里功能描述（feature），然后场景（scenario）每一步所对应steps.py 文件里的哪一行代码。

最后给出运行结果：
Feature(1 passed) 一个功能通过
Scenario(1 passed) 一个场景通过
Steps(3 passed) 三个步骤通过

第三节、添加测试场景

下面我们可以在 zero.feature 中多加几个场景（测试用例）：

Feature: Compute factorial
In order to play with Lettuce
As beginners
We'll implement factorial
Scenario: Factorial of 0
Given I have the number 0
When I compute its factorial
Then I see the number 1
Scenario: Factorial of 1
Given I have the number 1
When I compute its factorial
Then I see the number 1
Scenario: Factorial of 2
Given I have the number 2
When I compute its factorial
Then I see the number 2
Scenario: Factorial of 3
Given I have the number 3
When I compute its factorial
Then I see the number 6

运行结果：

嗯？?第四场景没通过，3！=321=6 这个预期结果肯定是正确的，那就是代码的逻辑有问题吧！如果你细心的话一定发现了 setup.py 中的代码并未真正实现阶乘，我们需要对它进行修改：