精选力扣500题 第38题 LeetCode 300.长递增子序列【c++/java详细题解】

1、题目

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7]是数组 [0,3,1,6,2,2,7]的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

进阶：

• 你可以设计时间复杂度为 $O(n2)$ 的解决方案吗？
• 你能将算法的时间复杂度降低到 $O(n\ast log(n))$ 吗?

2、思路1

(动态规划) $O(n^2)$

状态表示：f[i]表示以nums[i]为结尾的严格递增子序列的最大长度。

集合划分： 以nums[i]为结尾的严格递增子序列前一个数是nums[0]，nums[1],nums[i-1]，，，

状态计算： f[i] = max(f[i],f[j] + 1) (j

图示说明：

3、c++代码1

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int>f(n);
        int res = 0;
        for(int i = 0; i < n; i++)
        {
            f[i] = 1;
            for(int j = 0; j < i ; j++)
            {
                if(nums[j] < nums[i])
                {
                    f[i] = max(f[i],f[j] + 1);
                }
            }
            res = max(res,f[i]);
        }
        return res;
    }
};

4、java代码1

class Solution {
    public int lengthOfLIS(int[] nums) {
        int n = nums.length;
        int[] f = new int[n];
        int res = 0;
        for(int i = 0; i < n; i++)
        {
            f[i] = 1;
            for(int j = 0; j < i ; j++)
            {
                if(nums[j] < nums[i])
                {
                    f[i] = Math.max(f[i],f[j] + 1);
                }
            }
            res = Math.max(res,f[i]);
        }
        return res;
    }
}

5、思路2

(贪心+二分) $O(n\ast logn)$

如果我们要使上升子序列尽可能的长，则我们需要让序列上升得尽可能慢，因此我们希望每次在上升子序列最后加上的那个数尽可能的小。

因此我们维护一个数组q，让q[0]表示长度为1的最长上升子序列的末尾元素的最小值，q[1]表示长度为2的最长上升子序列的末尾元素的最小值，q[2]表示长度为3的最长上升子序列的末尾元素的最小值，，，，，

q数组一定是单调递增的，并且q数组中的值随着在q中的下标单调递增，那么所能维护的q数组的最大长度就是我们的答案。

我们遍历nums数组：

• 如果nums[i] > q.back(),直接将nums[i]插到q数组的末尾。

• 如果nums[i] <= q.back()并且 nums[i] <= q[0] ，说明nums[i]此时是最小的，让q[0] = x

• 如果nums[i] <= q.back()并且 nums[i] > q[0] ，我们在q数组中二分查找 < nums[i]的最大值，让nums[i]插到其后边。

  这样我们就可以让上升子序列最后加上的那个数尽可能的小。

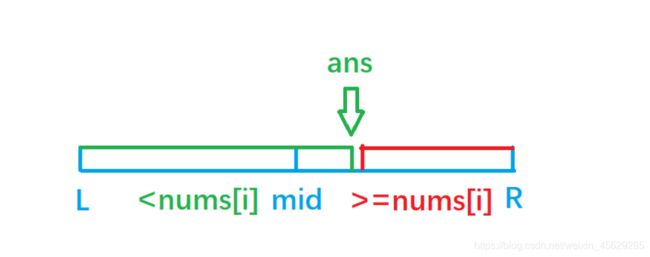
在[l,r]区间中，q[i]数组具有单调性，因此可以通过二分的最右边界找到< nums[i]的最大值的位置:

• q[mid] < nums[i]，往右半区域查找，l = mid
• q[mid] >= nums[i]，往左半区域查找，r = mid-1

图示：

6、c++代码2

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> q;
        for (auto x: nums) {
            if (q.empty() || x > q.back()) q.push_back(x);
            else {
                if (x <= q[0]) q[0] = x;
                else {
                    int l = 0, r = q.size() - 1;
                    while (l < r) {
                        int mid = l + r + 1 >> 1;
                        if (q[mid] < x) l = mid;
                        else r = mid - 1;
                    }
                    q[r + 1] = x;
                }
            }
        }
        return q.size();
    }
};

原题链接： 300.长递增子序列