计算机图形学基础2——光栅化

光栅化

视口变换之后，将三维空间中的多边形（多边形的顶点）变换到了屏幕空间，在屏幕上得到一个个网格（meshes）区间，接下来就要对网格进行光栅化，也就是将多边形拆成不同的像素，最终实现将图像绘制在屏幕上。

一般选择三角形作为计算机图形学中的基本图像形状，

MVP变换+视口变换之后就可以得到每个三角形网格在屏幕上的顶点坐标 ，接下来的操作就是将三角形变成真正的像素。

一、如何将三角形网格转变成真正的像素实现填充（光栅化）？

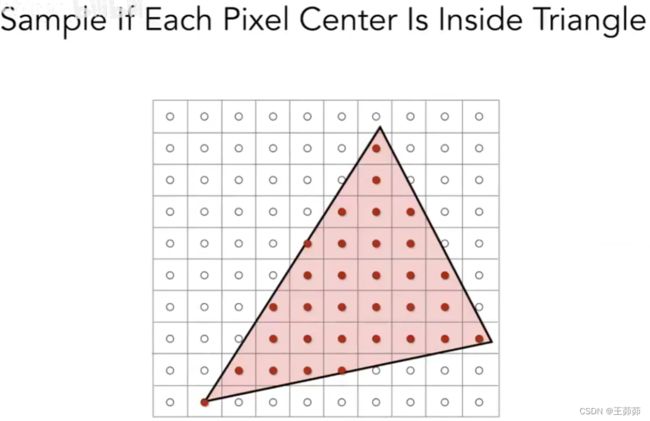
1、首先，要判断每个像素点（确切的说是像素中心点）与三角形和之间的位置关系

最简单的方法——采样Sampling

采样的概念：
给定一个连续函数，对其在某点处求值这个操作就是采样。采样相当于把一个函数离散化的过程。

具体操作：
在屏幕空间中定义一个inside函数，用像素中心坐标对该函数进行采样，用于判断像素点的中心是否在三角形内部。

（1）定义二元函数 inside (tri,x,y) ：tri表示要进行判断的三角形，x,y可以不是整型（2）采样方式： 对于屏幕上的每个像素点的中心进行inside函数计算，对每个像素点得到一个0,1值用于表示像素是否在三角形内部。

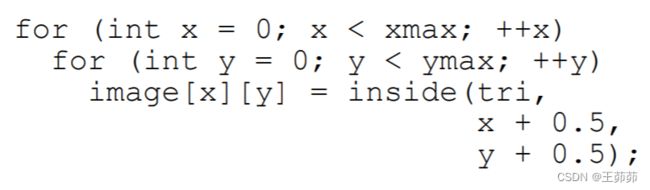
（3）采样函数的实现：
利用差积cross product判断一个点是否在三角形内部。具体数学知识见下面的参考链接。
参考链接：叉积的计算以及点是否在三角形内的判断方法

对在三角形边界上的特殊点可以自己定义规则，用于判断其是否归属于三角形。

（4）加速改进：
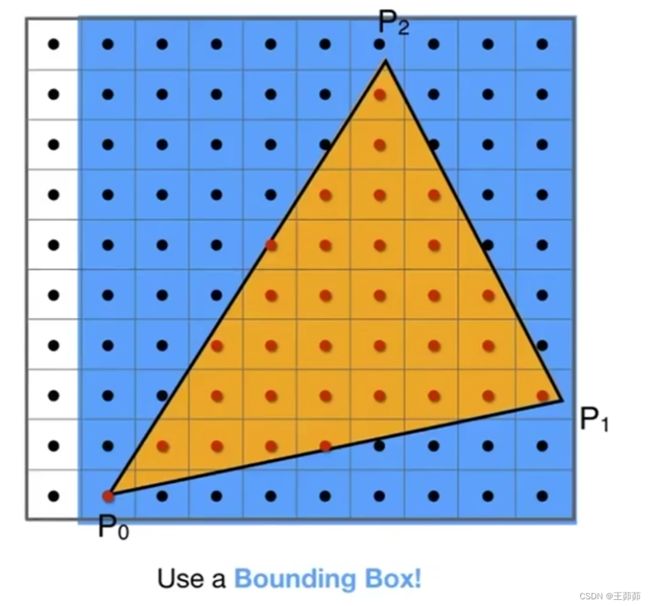
在前面第二步骤中，是对屏幕上的所有像素点判断其是否位于三角形内部从而进行采样计算，但是，试想一下，其实一个三角形可以覆盖的范围是有限的，有些屏幕上的像素点距离三角形较远无需进行额外的采样判断。

因此，定义一个概念——三角形“包围盒bounding box”。三角形包围盒非常好计算：屏幕空间中的每个三角形，三个顶点的坐标已知，对其x坐标取最小最大值，纵坐标取最小最大值即可得到该三角形的bbx。

对于不在该区域的像素点就无须对该三角形进行采样计算。

实际的屏幕光栅化的方法

在计算机图形学中我们就假设像素是一个个小方块，并且其颜色不可分割。
上述最简单的采样光栅化方法处理完之后，得到如下图所示的结果，可以发现因为像素是小方块，所以最终光栅化的结果并不是我们希望的三角形，而是存在很多锯齿（Jaggies）的形状。

二、抗锯齿（Antialiasing）和深度缓冲（Z-Buffering）

概念：锯齿（Jaggies）的学名叫做走样（Aliasing），解决锯齿问题就叫做反走样（Antialiasing）。

采样错误（Sampling Artifacts）

所有采样操作带来的问题统称采样Artifacts。列举几个采样错误如下：

• 锯齿Jaggies
• 摩尔纹Moire Patterns
• 车轮效应Wagon Wheel Illusion

采样错误出现的本质是：信号的变化太快，但是采样的速度相对较慢。

反走样 （Antialiasing）

如何实现反走样（也就是解决锯齿问题）？
在采样之前先进行一个模糊化操作Blurring，也就是先对图像进行滤波（Pre-Filtering），然后在模糊化之后的栅格化三角形的边缘的点的像素值取中间值。

从频率的角度如何理解？

涉及知识介绍：

频域Frequency Domain

上述图中，f称为频率，频率控制函数值变化的快慢。f越大，函数值变的越快。
周期T与频率f互为倒数。

傅里叶变换fourier Transform
傅里叶级数展开： 任何一个周期函数都可以写成sin，cos以及一个常数项的组合。
如下图所示，坐标轴中的黑色的折线表示的函数可以使用cos函数的组合近似表示。当cos项逐渐增加时，可以无限接近原函数曲线。

傅里叶变换： 傅里叶变换从傅里叶级数展开发展而来，但是傅里叶级数展开仅限于周期函数，傅里叶变换的应用不仅限于周期函数，也适用于非周期函数。给定一个函数都可以通过一个变换变成另一种由sin和cos函数组合的形式（空间域—>频域），并且可以通过另一个变换函数实现逆变换。

\
傅里叶变换可以实现将一个函数变成不同的频率的段。
\

高频率的函数需要更高频率的采样。 如下图所示，函数5的频率很高，但是如果使用低频的采样，则无法很好的复原原始函数图像。

使用相同的采样方法采样两种不同频率的函数的到的结果相同，这种情况就叫“走样aliases”。

傅里叶变换可以实现将一个函数从时域变换到频域。

Filtering

在频率角度理解，Filtering就是去掉一些特定的频率的内容。

图像的频率又称为空间频率，它反映了图像的像素灰度在空间中变化的情况。例如，一面墙壁的图像，由于灰度值分布平坦，其低频成分就较强，而高频成分较弱；而对于国际象棋棋盘或者沟壑纵横的卫星图片这类具有快速空间变化的图像来说，其高频成分会相对较强，低频则较弱。

利用傅里叶变换将一张图从时域（图像空间）转换到频域进行展示：

位于中心位置的是低频数据，周围是高频区域，由中心到四边频率越来越高。
亮度用于表示该区域的信息量。如下图所示，中心位置（低频区域）亮度更亮，也就是说图像中存在更多的低频信息。


对图像进行一些频率滤波之后的结果进行展示：
左上角可以看到，过滤掉频率图中的大部分低频信息之后，逆傅里叶变换之后得到的图像中仅存在一些边缘信息，这是因为物体边缘的图像灰度值变化较大，对应的频率越高。

换一种角度，可以将Filtering理解为Convolution（Average）。
如下图所示，（定理：时域的卷积等于频域的乘积）

Sampling

从频率的角度理解采样：Sampling=Repeating Frequency Contents。采样就是重复原始信号的频谱。

如下图所示，利用b对a进行采样得到c，可以看到，信号c的频率分布式信号a的频率在采样点进行复制之后的结果。

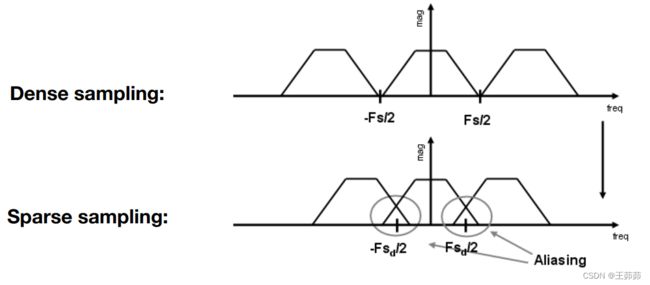
Aliasing

从频率的角度理解走样：Aliasing = Mixed Frequency Contents，走样就是采样过于稀疏时导致频率重叠。

Antialiasing

1、如何降低走样错误（Aliasing Error）？

• Option1：提高采样率

  • 直接增加了在频域中的频率副本之间的距离。
  • 需要更高分辨率的显示器，传感器，帧缓冲…
  • 代价：昂贵&可能需要非常高的分辨率；并不算是解决走样错误的方法。

• Option2：反走样Antialiasing

  • 先把高频信息去掉然后再进行采样
  • 先做模糊操作-然后再采样
    

2、反走样具体实现？

（1）实际如何使用滤波器进行Filtering（如何将三角形变成模糊三角形）？

在原始图像上进行卷积操作，

最简单的，使用一个1 pixel-width 的滤波核，一个像素的滤波核比较小因此属于低通滤波器，可以起到模糊操作。
Antialiasing By Averaging Values in Pixel Area，对于每个像素单位，利用该像素点中的三角形的覆盖面对该像素区域求一个颜色的平均作为该像素点滤波之后的像素值，如下图所示：

（2）如何实现上述1 pixel filter？
利用Supersampling（MSAA）方法。

对像素点进行划分，