数据结构与算法—冒泡排序&快速排序
目录
一、交换排序
二、冒泡排序
时间复杂度
三、快速排序
1、三种一次划分操作
Hoare法
挖洞法
前后指针法
三种方法总结:
2、改进划分效率
3、递归实现快速排序
4、非递归实现快速排序
栈的函数:
非递归排序函数:
5、时间复杂度
完整代码:
声明头文件:
排序函数:
测试函数:
一、交换排序
基本思想:所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。主要包括:冒泡排序和快速排序
二、冒泡排序
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; ++j)
{
bool exchange = false;
for (int i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
int tmp = a[i];
a[i] = a[i - 1];
a[i - 1] = tmp;
exchange = true;
}
}
if (exchange == false)
{
break;
}
}
}冒泡排序使用了两个循环,外层循环控制排序的轮数,内层循环控制每轮排序的次数。每轮排序都会将未排序部分的最大值交换到未排序部分的最后面,因此每轮排序都会将未排序部分的长度减1
- 代码中的变量 j 表示已排序部分的长度,初始值为0,每轮排序结束后 j 的值加1。
- 内层循环从第一个元素开始,依次比较相邻的两个元素,如果它们的顺序错误就交换它们的位置。
- 如果在一轮排序中没有发生任何交换,说明已经排好序了,可以直接退出循环。
时间复杂度
这个算法的时间复杂度是O(n^2),因为它需要进行n轮排序,每轮排序需要比较n-j-1次相邻的元素,因此总共需要比较(n-1)+(n-2)+...+1=n*(n-1)/2次。
三、快速排序
快速排序是一种交换排序方法,由Hoare于1962年提出。它使用二叉树结构来进行排序,
基本思想:
- 从待排序元素序列中任选一个元素作为基准值,按照该元素的排序码将待排序集合分割成两个子序列。
- 左子序列中的所有元素都小于基准值,右子序列中的所有元素都大于基准值。
- 然后,对左右子序列分别重复该过程,直到所有元素都排列在相应位置上为止。
我们以数组第一个元素6为基准值key,通过动图来体会一下划分一次的过程。
在每次分割过程中,选择一个基准值,将序列中的元素按照基准值的大小分割成两个子序列。然后,对这两个子序列分别进行递归排序,最终将它们合并起来,就可以得到一个有序的序列。
1、三种一次划分操作
接下来我们对三种快排的方法进行讲解:
Hoare法
通过动图来体会一下Hoare法划分一次的过程。
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
int PartSort1(int* a, int left, int right)
{
int keyi = left;
while (left < right) {
//右边找小
while (left < right && a[right] >= a[keyi]) {
right--;
}
//左边找大
while (left < right && a[left] <= a[keyi]) {
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
return left;
}
- 函数中使用了两个指针 left 和 right,它们分别指向区间的左右两端。
- 首先将基准值keyi赋值为left。
代码首先判断left是否小于right,如果不是,则说明当前子序列已经比较完毕,可以退出循环。
接着,代码判断a[right]是否大于等于a[keyi],如果是,则说明a[right]比关键元素大或者相等,需要继续向左查找比关键元素小的元素。因此,right指针向左移动一位,继续比较下一个元素。
- 在内层循环中,首先从右侧开始,代码先判断left是否小于right,如果不是,则说明当前子序列已经比较完毕,可以退出循环。接着,代码判断a[right]是否大于等于a[keyi],如果是,则说明a[right]比关键元素大或者相等,需要继续向左查找比关键元素小的元素。
- 如果找到第一个小于基准值 a[keyi] 的元素,从左侧开始,继续找到第一个大于基准值的元素。接着,交换这两个元素的位置,使得左侧元素小于等于基准值,右侧元素大于等于基准值。重复这个过程,直到 left 和 right 指针相遇。
- 如果left和right相遇,则退出循环,将关键元素 a[keyi] 与 left 指针所指向的元素交换位置,使得基准值位于分区的中间位置。这样,分区函数 PartSort1 就完成了它的任务。
- 最后,交换a[keyi]和a[left]的值,返回基准值 a[keyi] 排序后的位置 left 。
- 需要注意的是,函数 PartSort1 返回了 left 指针的值,这个值表示基准值在分区后的位置。在快速排序算法中,这个值会被用来确定下一次分区的区间范围。
- 另外,函数中使用了一个 Swap 函数,用于交换两个指针所指向的元素的值。这个函数的作用是使代码更加简洁和易读,避免了重复的代码。
挖洞法
通过动图来体会一下挖洞法划分一次的过程。
int PartSort2(int* a, int left, int right)
{
int key = a[left];
int hole = left;
while (left < right) {
while (left < right && a[right] >= key) {
right--;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= key) {
left++;
}
a[hole] = a[left];
hole = right;
}
a[hole] = key;
return hole;
}
- 首先,定义了一个名为PartSort2的函数,该函数接受三个参数:一个整型数组a,以及左右两个下标left和right,表示要排序的数组a的左右边界。
- 定义了一个名为key的变量,用于存储左边界位置的元素值,即a[left]的值。定义了一个名为hole的变量,用于记录当前空缺的位置,初始值为left。
- 进入while循环,当left小于right时,执行以下操作:
- 在循环中,先从右边开始找到第一个小于key的元素,将其下标赋值给right。将a[right]的值赋值给a[hole],即将右边界位置的元素放到空缺的位置上。将hole的值更新为right,即将空缺位置的下标更新为右边界位置的下标。
- 接着,从左边开始找到第一个大于key的元素,将其下标赋值给left。将a[left]的值赋值给a[hole],即将左边界位置的元素放到空缺的位置上。将hole的值更新为left,即将空缺位置的下标更新为左边界位置的下标。
- 循环结束后,将key的值赋值给a[hole],即将key放到空缺的位置上。
- 最后,返回hole的值,即返回key在数组a中的位置。
前后指针法
通过动图来体会一下前后指针法划分一次的过程。
思路:
- 最开始prev和cur相邻的,
- 当cur遇到比key的大的值以后,cur移动prev不动,他们之间的值都是比key大的值
- cur找小,找到小的以后,跟prev位置的值交换,然后prev后移一位。
- 相当于把大翻滚式往右边推,同时把小的换到左边
int PartSort3(int* a, int left, int right)
{
int prev = left;
int cur = left + 1;
int keyi = left;
while (cur <= right){
if (a[cur] < a[keyi] && ++prev != cur){
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
- 首先,定义了一个名为PartSort3的函数,该函数接受三个参数:一个整型数组a,以及左右两个下标left和right,表示要排序的数组a的左右边界。
- 定义了三个变量:prev、cur和keyi,分别表示当前处理的位置、当前遍历的位置和关键元素的位置,初始值均为left。
- 进入while循环,当cur小于等于right时,执行以下操作:
- 如果a[cur]小于a[keyi],则将prev的值加1,并将a[prev]和a[cur]交换位置,即将小于关键元素的元素放到前面。
- 将cur的值加1,继续遍历数组。
- 循环结束后,将a[prev]和a[keyi]交换位置,即将关键元素放到正确的位置上。
- 将keyi的值更新为prev,即将关键元素的位置更新为当前的位置。
- 最后,返回keyi的值,即返回关键元素在数组a中的位置。
三种方法总结:
-
PartSort1函数:该函数采用的是左右指针法,即从左右两端开始遍历数组,将小于关键元素的元素放到左边,大于关键元素的元素放到右边,最后将关键元素放到正确的位置上。该函数的时间复杂度为O(nlogn)。
-
PartSort2函数:该函数采用的是挖坑填数法,即先将关键元素挖出来,然后从右边开始找到第一个小于关键元素的元素,将其放到左边的空位上,再从左边开始找到第一个大于关键元素的元素,将其放到右边的空位上,最后将关键元素放到正确的位置上。该函数的时间复杂度为O(nlogn)。
-
PartSort3函数:该函数采用的是前后指针法,即从左到右遍历数组,将小于关键元素的元素放到前面,大于关键元素的元素放到后面,最后将关键元素放到正确的位置上。该函数的时间复杂度为O(n)。
总体来说,这三种函数都是快速排序算法中的重要组成部分,它们的实现方式不同,但本质上都是通过将小于关键元素的元素放到前面,大于关键元素的元素放到后面,来实现对数组的排序。在实际应用中,可以根据具体情况选择不同的函数来实现快速排序算法。
2、改进划分效率
但是这样每次都已区间最左位置的元素为基准值 ,可能会导致排序效率很低。
这是因为在某些情况下,选择的基准值可能会导致划分后的两个子序列长度差别很大,从而使得快速排序算法的时间复杂度退化为O(n^2)。
例如:如果待排序的数组已经是有序而且是升序的,而每次选择的基准值都是区间最左位置的元素,那么每次划分后的左子序列都为空,右子序列都包含了原数组中的所有元素,这样就会导致快速排序算法的时间复杂度退化为O(n^2)。
为了避免这种情况,可以采用一些优化策略,如三数取中法、随机化等。
- 三数取中法是指在区间的左、中、右三个位置分别取出一个数,然后将它们排序,取中间值作为基准值。这样可以避免选择到极端值作为基准值,从而提高快速排序算法的效率。
- 随机化则是指在待排序的数组中随机选择一个元素作为基准值,这样可以使得每次划分后的两个子序列长度差别更小,从而提高快速排序算法的效率。
实际中我们更推荐三数取中法,它的效率会更好一点。
通过该代码实现找到区间中的中位数, 代码如下:
int GetMidIndex(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if (a[left] < a[right])
{
return right;
}
else
{
return left;
}
}
else // a[left] > a[mid]
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[left] > a[right])
{
return right;
}
else
{
return left;
}
}
}接下来将中位数运用到Hoare法函数PartSort3中:(挖洞和Hoare方法操作相同)
int PartSort3(int* a, int left, int right)
{
//获取中位数
int midi = GetMidIndex(a, left, right);
//将中位数的值与left交换
Swap(&a[left], &a[midi]);
int prev = left;
int cur = left + 1;
int keyi = left;
while (cur <= right){
if (a[cur] < a[keyi] && ++prev != cur){
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}3、递归实现快速排序
排序一个区间的函数PartSort1我们写完后,应该将它运用起来,通过递归思想对每个划分区间进行排序,从而实现快速排序。
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = PartSort1(a, begin, end);
//每次划分范围 [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
- QuickSort函数是快速排序算法的入口函数,它接受一个整型数组a、数组的起始下标begin和结束下标end作为参数。
- 在函数内部,首先判断递归结束条件—begin和end的大小关系,如果begin大于等于end,分别代表“区间不存在”和”区间只有一个值“,则直接结束当前递归,
- 否则调用PartSort1函数对数组进行一次划分操作,将数组a中的元素分为两部分,一部分小于等于a[keyi],另一部分大于a[keyi],并返回a[keyi]在排序后的位置。
- 然后,递归调用QuickSort函数对左半部分和右半部分进行排序,直到整个数组有序。
这个递归版本的快速排序算法。与非递归版本相比,它的实现更加简单,但是可能会因为递归调用的深度过大而导致栈溢出的问题。
接下来我们来看看非递归如何实现快速排序:
4、非递归实现快速排序
我们将待排序数组的起始位置和结束位置入栈,然后不断地从栈中取出两个位置,对这两个位置之间的元素进行分区操作,得到基准元素的位置,然后将基准元素左右两边的子数组的起始位置和结束位置入栈,以便后续处理。这样就可以避免递归调用带来的额外开销,提高了快速排序的效率。
栈的函数:
#include
#include
#include
typedef int STDataType;
typedef struct Stack
{
STDataType* a;
int top;
int capacity;
}ST;
void STInit(ST* pst);
void STDestroy(ST* pst);
void STPush(ST* pst, STDataType x);
void STPop(ST* pst);
STDataType STTop(ST* pst);
bool STEmpty(ST* pst);
int STSize(ST* pst);
void STInit(ST* pst)
{
assert(pst);
pst->a = NULL;
pst->top = 0;
pst->capacity = 0;
}
void STDestroy(ST* pst)
{
assert(pst);
free(pst->a);
pst->a = NULL;
pst->top = pst->capacity = 0;
}
void STPush(ST* pst, STDataType x)
{
if (pst->top == pst->capacity)
{
int newCapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDataType* tmp = (STDataType*)realloc(pst->a, newCapacity * sizeof(STDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
pst->a = tmp;
pst->capacity = newCapacity;
}
pst->a[pst->top] = x;
pst->top++;
}
void STPop(ST* pst)
{
assert(pst);
assert(!STEmpty(pst));
pst->top--;
}
STDataType STTop(ST* pst)
{
assert(pst);
assert(!STEmpty(pst));
return pst->a[pst->top - 1];
}
bool STEmpty(ST* pst)
{
assert(pst);
return pst->top == 0;
}
int STSize(ST* pst)
{
assert(pst);
return pst->top;
} 非递归排序函数:
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
STInit(&st);
STPush(&st, end);
STPush(&st, begin);
while (!STEmpty(&st))
{
int left = STTop(&st);
STPop(&st);
int right = STTop(&st);
STPop(&st);
//PartSort3也可以,讲解基于PartSort1
//int keyi = PartSort3(a, left, right);
int keyi = PartSort1(a, left, right);
if (keyi + 1 < right)
{
STPush(&st, right);
STPush(&st, keyi + 1);
}
if (left < keyi-1)
{
STPush(&st, keyi-1);
STPush(&st, left);
}
}
STDestroy(&st);
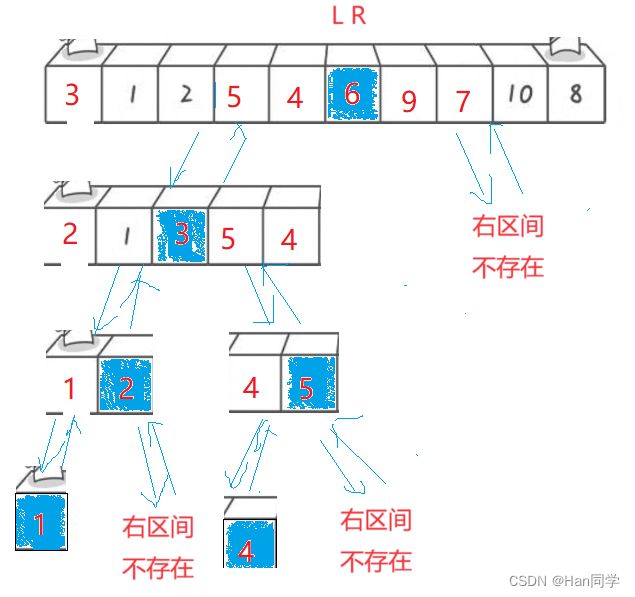
}下面是对left到key部分(即第一个基准值key的左部分)进行操作的过程:
ST是一个栈的结构体,STInit、STPush、STPop和STEmpty分别是初始化栈、入栈、出栈和判断栈是否为空的函数。PartSort1是快速排序中的分区函数,用于将数组分成两个部分。具体来说,PartSort1函数选择数组的最后一个元素作为基准元素,然后将小于基准元素的元素放在数组的左边,大于基准元素的元素放在数组的右边,最后返回基准元素的位置。
- 初始化一个空栈,将待排序数组的开始和结束位置入栈。
- 进入一个循环,条件是栈不为空。在每次循环中:
- 从栈顶取出一个元素,作为当前子数组的开始位置,再从栈顶取出一个元素,作为当前子数组的结束位置。
- 调用
PartSort1函数,对当前子数组进行一次快速排序的划分,返回划分元素的位置。这个函数的作用是找到一个元素(划分元素),使得它左边的所有元素都小于它,它右边的所有元素都大于它。- 如果划分元素的右边还有元素(即
keyi + 1 < right),则将右边子数组的开始和结束位置入栈。- 如果划分元素的左边还有元素(即
left < keyi-1),则将左边子数组的开始和结束位置入栈。- 当栈为空时,所有子数组都已经排序完成,算法结束,销毁栈。
5、时间复杂度
递归和非递归版本的快速排序算法的时间复杂度是一样的,都是在平均情况下O(n log n),在最坏情况下O(n^2)。
这是因为每次划分都将数组分成了两个部分,每个部分的长度大约是原数组长度的一半,因此需要进行log n次划分才能完成排序。在每次划分中,需要遍历整个数组,时间复杂度是O(n)。因此,快速排序的平均时间复杂度是O(n log n)。
完整代码:
声明头文件:
#include
#include
#include
void PrintArray(int* a, int n);
void BubbleSort(int* a, int n);
void QuickSort(int* a, int begin, int end);
void QuickSortNonR(int* a, int begin, int end);
排序函数:
#include "sort.h"
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; i++) {
printf("%d ", a[i]);
}
printf("\n");
}
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; ++j)
{
bool exchange = false;
for (int i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
int tmp = a[i];
a[i] = a[i - 1];
a[i - 1] = tmp;
exchange = true;
}
}
if (exchange == false)
{
break;
}
}
}
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
int GetMidIndex(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid]) {
if (a[mid] < a[right]) {
return mid;
}
else if (a[left] < a[right]) {
return right;
}
else {
return left;
}
}
else {//a[left]>a[mid]
if (a[mid] > a[right]) {
return mid;
}
else if (a[left] < a[right]) {
return left;
}
else {
return right;
}
}
}
// hoare
// [left, right]
int PartSort1(int* a, int left, int right)
{
int midi = GetMidIndex(a, left, right);
Swap(&a[left], &a[midi]);
int keyi = left;
while (left < right) {
//右边找小
while (left < right && a[right] >= a[keyi]) {
right--;
}
while (left < right && a[left] <= a[keyi]) {
left++;
}
Swap(&a[left], &a[right]);
}
Swap(&a[keyi], &a[left]);
return left;
}
// 挖坑法
// [left, right]
int PartSort2(int* a, int left, int right)
{
int midi = GetMidIndex(a, left, right);
Swap(&a[left], &a[midi]);
int key = a[left];
int hole = left;
while (left < right) {
while (left < right && a[right] >= key) {
right--;
}
a[hole] = a[right];
hole = right;
while (left < right && a[left] <= key) {
left++;
}
a[hole] = a[left];
hole = right;
}
a[hole] = key;
return hole;
}
// 前后指针法
// [left, right]
int PartSort3(int* a, int left, int right)
{
int midi = GetMidIndex(a, left, right);
Swap(&a[left], &a[midi]);
int prev = left;
int cur = left + 1;
int keyi = left;
while (cur <= right){
if (a[cur] < a[keyi] && ++prev != cur){
Swap(&a[prev], &a[cur]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
return keyi;
}
// 时间复杂度: O(logN*N)
// 空间复杂度:O(logN)
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return;
int keyi = PartSort3(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
QuickSort(a, begin, keyi - 1);
QuickSort(a, keyi + 1, end);
}
测试函数:
#include"Sort.h"
#include
//测试排序
void TestBubbleSort()
{
int a[] = { 4,7,1,9,3,6,5,8,3,2,0 };
PrintArray(a, sizeof(a) / sizeof(int));
BubbleSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
void TestQuickSort()
{
//int a[] = { 4,7,1,9,3,6,5,8,3,2,0 };
int a[] = { 6,1,2,7,9,3,4,5,10,8 };
PrintArray(a, sizeof(a) / sizeof(int));
QuickSort(a, 0, sizeof(a) / sizeof(int) - 1);
PrintArray(a, sizeof(a) / sizeof(int));
}
//测试运行效率
void TestOP()
{
srand(time(0));
const int N = 1000000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
int begin1 = clock();
BubbleSort(a1, N);
int end1 = clock();
int begin2 = clock();
QuickSort(a2, 0, N - 1);
int end2 = clock();
printf("BubbleSort:%d\n", end1 - begin1);
printf("QuickSort:%d\n", end2 - begin2);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
}
int main()
{
//TestBubbleSort();
//TestQuickSort();
//estOP();
return 0;
}