Openssl 1024bit RSA算法---公私钥获取和处理（一）

1.简介

使用OpenSSL生成公私钥文件，然后再将文件中的信息读出的操作。

由于要对设备升级，需要用到RSA算法对一部分验证信息进行加密.

2.使用OpenSSL获取公私钥

我在window系统尝试安装OpenSSL，但是安装不上，我们可以使用linux自带的OpenSSL自动生成公私钥（我这里使用的Ubuntu）

打开终端，依次输入一下命令就可以生成我们想要的文件（生成文本文件，是为了便于查看文件内容；生成bin文件是为了接下来的文件操作）

//生成1024位的私钥
openssl genrsa -out private.pem 1024
 
//将生成的文件转换为文本
openssl rsa -in private.pem -text -out private.txt
 
//将BASE64编码的文件转换为bin文件
openssl   base64  -d  -in private.pem -out private.bin

详细关于私钥（PEM格式）参考：OPENSSL中RSA私钥文件（PEM格式）解析【一】 - 走看看

3.文件处理

3.1秘钥信息获取

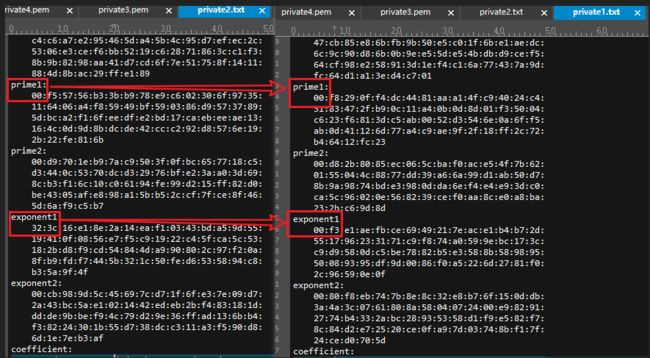
通过查看生成的文本文件发现，不同的文件生成的文件长度不一样，有些会在头部自动添加一个“00”

为了解决不同文件的差异，消除“00”的影响，文件处理流程如下：

 上面的步骤还有uint32_t bits的位还没有设定，由于我们生成的1024bit的秘钥，所以我们将bits的值设为1024.如下所示的结构体，就是RSA私钥断开

//上面的流程主要是将生成的秘钥按格式填入
typedef struct
{
    uint32_t bits;                   /* length in bits of modulus */
    uint8_t  modulus[256];           /* modulus */
    uint8_t  publicExponent[4];      /* public exponent */
    uint8_t  exponent[256];          /* private exponent */
    uint8_t  prime[2][128];          /* prime factors */
    uint8_t  primeExponent[2][128];  /* exponents for CRT */
    uint8_t  coefficient[128];       /* CRT coefficient */ 
} R_RSA_PRIVATE_KEY;

3.2公钥信息获取 

typedef struct
{
    uint32_t bits;                   /* length in bits of modulus */
    uint8_t  modulus[256];           /* modulus */
    uint8_t  exponent[4];            /* public exponent */ 
} R_RSA_PUBLIC_KEY;

4.读取文件公私钥信息

#ifndef READ_PEM_FILE_H
#define READ_PEM_FILE_H
#include "file.h"
#include "s_rsa.h"
 
 
void generate_private_and_public_key(R_RSA_PRIVATE_KEY* privat_key, R_RSA_PUBLIC_KEY* public_key);
 
#endif

#include "read_pem_file.h"
 
 
 
static int is_private_pem_exist(void)//判断当前文件下有没有private.pem
{
    if(fopen("private.bin", "r"))
    {
        return 1;
    }
    else
    {
        printf("\n当前文件未找到private.bin这个文件，请用openssl工具生成\n\n");
        return 0;
    }
}
 
//从文件中读取私钥信息
static void read_private_pem(R_RSA_PRIVATE_KEY* privat_key)
{
    int i = 0;
    long long file_size = 0;
    char* flie_buffer;
    if(is_private_pem_exist() == 1)
    {
        flie_buffer = copyFile("private.bin", &file_size);
    }
    else
    {
        system("pause");
        exit(0);
    }
 
    //printf("%02x\n\n", file_size);
 
    //for(i = 1; i<= file_size; i++)
    //{
    //  printf("%02x ", (unsigned char)flie_buffer[i - 1]);
    //  if(i % 16 == 0)
    //  {
    //      printf("\n");
    //  }
    //}
 
 
 
    flie_buffer += 10;
    if(*flie_buffer == 0)
    {
        flie_buffer += 1;
    }
    for(i = 0; i < 128; i++)
    {
        privat_key->modulus[i] = flie_buffer[i];
    }
    flie_buffer += 127;
 
    flie_buffer += 3;
    if(*flie_buffer == 0)
    {
        flie_buffer += 1;
    }
    for(i = 0; i < 3; i++)
    {
        privat_key->publicExponent[i + 1] = flie_buffer[i];
    }
    flie_buffer += 2;
 
    flie_buffer += 4;
    if(*flie_buffer == 0)
    {
        flie_buffer += 1;
    }
    for(i = 0; i < 128; i++)
    {
        privat_key->exponent[i] = flie_buffer[i];
    }
    flie_buffer += 127;
 
    flie_buffer += 3;
    if(*flie_buffer == 0)
    {
        flie_buffer += 1;
    }
    for(i = 0; i < 64; i++)
    {
        privat_key->prime[0][i] = flie_buffer[i];
    }
    flie_buffer += 63;
 
    flie_buffer += 3;
    if(*flie_buffer == 0)
    {
        flie_buffer += 1;
    }
    for(i = 0; i < 64; i++)
    {
        privat_key->prime[1][i] = flie_buffer[i];
    }
    flie_buffer += 63;
 
    flie_buffer += 3;
    if(*flie_buffer == 0)
    {
        flie_buffer += 1;
    }
    for(i = 0; i < 64; i++)
    {
        privat_key->primeExponent[0][i] = flie_buffer[i];
    }
    flie_buffer += 63;
 
    flie_buffer += 3;
    if(*flie_buffer == 0)
    {
        flie_buffer += 1;
    }
    for(i = 0; i < 64; i++)
    {
        privat_key->primeExponent[1][i] = flie_buffer[i];
    }
    flie_buffer += 63;
 
    flie_buffer += 3;
    if(*flie_buffer == 0)
    {
        flie_buffer += 1;
    }
    for(i = 0; i < 64; i++)
    {
        privat_key->coefficient[i] = flie_buffer[i];
    }
}
 
//打印私钥信息
static void prinf_privat_key(R_RSA_PRIVATE_KEY* privat_key)
{
    int i = 0;
    printf("\nmoduls:\n");
    for(i = 1; i <= 128; i++)
    {
        printf("%02x ",privat_key->modulus[i - 1]);
        if(i % 16 == 0)
        {
            printf("\n");
        }
    }
 
    printf("\npubicExpinent:\n");
    for(i = 0; i < 4; i++)
    {
        printf("%02x ",privat_key->publicExponent[i]);
    }
 
    printf("\nprivateExponent:\n");
    for(i = 1; i <= 128; i++)
    {
        printf("%02x ",privat_key->exponent[i - 1]);
        if(i % 16 == 0)
        {
            printf("\n");
        }
    }
 
    printf("\nprime1:\n");
    for(i = 1; i <= 64; i++)
    {
        printf("%02x ",privat_key->prime[0][i - 1]);
        if(i % 16 == 0)
        {
            printf("\n");
        }
    }
 
    printf("\nprime2:\n");
    for(i = 1; i <= 64; i++)
    {
        printf("%02x ",privat_key->prime[1][i - 1]);
        if(i % 16 == 0)
        {
            printf("\n");
        }
    }
 
    printf("\nexponent1:\n");
    for(i = 1; i <= 64; i++)
    {
        printf("%02x ",privat_key->primeExponent[0][i - 1]);
        if(i % 16 == 0)
        {
            printf("\n");
        }
    }
 
    printf("\nexponent2:\n");
    for(i = 1; i <= 64; i++)
    {
        printf("%02x ",privat_key->primeExponent[1][i - 1]);
        if(i % 16 == 0)
        {
            printf("\n");
        }
    }
 
    printf("\ncoefficient:\n");
    for(i = 1; i <= 64; i++)
    {
        printf("%02x ",privat_key->coefficient[i - 1]);
        if(i % 16 == 0)
        {
            printf("\n");
        }
    }
     
}
 
//填充bits以及给公钥赋值
//生成公钥，私钥
void generate_private_and_public_key(R_RSA_PRIVATE_KEY* privat_key, R_RSA_PUBLIC_KEY* public_key)
{
    public_key->bits = 1024;
    privat_key->bits = 1024;
 
    read_private_pem(privat_key);
    prinf_privat_key(privat_key);//读出私钥信息
 
    for(int i = 0; i < 4; i++)
    {
        public_key->exponent[i] = privat_key->publicExponent[i];
    }
    for(int i = 0; i < 256; i++)
    {
        public_key->modulus[i] = privat_key->modulus[i];
    }
}

 5. RSA标准算法

#ifndef S_RSA_H_
#define S_RSA_H_
 
typedef unsigned char uint8_t;
typedef unsigned int  uint32_t;
// ����ֵ����
#define RE_DATA 0x0401
#define RE_LEN  0x0406
 
/* RSA key lengths.
 */
#define MIN_RSA_MODULUS_BITS 508
/* #define MAX_RSA_MODULUS_BITS 1024 ** linq modify ->>2048 ***/
#define MAX_RSA_MODULUS_BITS 2048
#define MAX_RSA_MODULUS_LEN ((MAX_RSA_MODULUS_BITS + 7) / 8)
#define MAX_RSA_PRIME_BITS ((MAX_RSA_MODULUS_BITS + 1) / 2)
#define MAX_RSA_PRIME_LEN ((MAX_RSA_PRIME_BITS + 7) / 8)
 
/* Length of digit in bits */
#define NN_DIGIT_BITS 32
#define NN_HALF_DIGIT_BITS 16
/* Length of digit in bytes */
#define NN_DIGIT_LEN (NN_DIGIT_BITS / 8)
/* Maximum length in digits */
#define MAX_NN_DIGITS \
  ((MAX_RSA_MODULUS_LEN + NN_DIGIT_LEN - 1) / NN_DIGIT_LEN + 1)
/* Maximum digits */
#define MAX_NN_DIGIT 0xffffffff
#define MAX_NN_HALF_DIGIT 0xffff
 
/* Macros.
 */
#define LOW_HALF(x) ((x) & MAX_NN_HALF_DIGIT)
#define HIGH_HALF(x) (((x) >> NN_HALF_DIGIT_BITS) & MAX_NN_HALF_DIGIT)
#define TO_HIGH_HALF(x) (((NN_DIGIT)(x)) << NN_HALF_DIGIT_BITS)
#define DIGIT_MSB(x) (uint32_t)(((x) >> (NN_DIGIT_BITS - 1)) & 1)
#define DIGIT_2MSB(x) (uint32_t)(((x) >> (NN_DIGIT_BITS - 2)) & 3)
 
#define NN_ASSIGN_DIGIT(a, b, digits) {NN_AssignZero (a, digits); a[0] = b;}
#define NN_EQUAL(a, b, digits) (! NN_Cmp (a, b, digits))
#define NN_EVEN(a, digits) (((digits) == 0) || ! (a[0] & 1))
 
 
typedef struct     // ��Կ�ṹ
{
    uint32_t bits;                   /* length in bits of modulus */
    uint8_t  modulus[256];           /* modulus */
    uint8_t  exponent[4];            /* public exponent */ 
} R_RSA_PUBLIC_KEY;
 
typedef struct    // ˽Կ�ṹ
{
    uint32_t bits;                   /* length in bits of modulus */
    uint8_t  modulus[256];           /* modulus */
    uint8_t  publicExponent[4];      /* public exponent */
    uint8_t  exponent[256];          /* private exponent */
    uint8_t  prime[2][128];          /* prime factors */
    uint8_t  primeExponent[2][128];  /* exponents for CRT */
    uint8_t  coefficient[128];       /* CRT coefficient */ 
} R_RSA_PRIVATE_KEY;
 
 
int  rsa_public(void *outbuf, int *outlen, const void *inbuf, int inlen, const R_RSA_PUBLIC_KEY *pubkey);
int  rsa_private(void *outbuf, int *outlen, const void *inbuf, int inlen, const R_RSA_PRIVATE_KEY *prikey);
 
#endif

#include 
#include 
#include 
#include "s_rsa.h"
 
typedef uint32_t NN_DIGIT;
typedef uint16_t NN_HALF_DIGIT;
 
/****************************************************************************
  ??????     :  void dmult(uint32_t a, uint32_t b, uint32_t *cHigh, uint32_t *cLow)
  ????       :  32λ???????????
****************************************************************************/
void dmult(uint32_t a, uint32_t b, uint32_t *cHigh, uint32_t *cLow)
{
    uint64_t temp1,temp2,temp3;
 
    temp1 = a;
    temp2 = b;
 
    temp3 = temp1*temp2;
 
    *cHigh = temp3>>32;
    *cLow = temp3;
}
 
/****************************************************************************
  ??????     :
  ????       :
  ???????   :
  ???????   :
  ?????     :
  ??????   :
      ?????     ??????    ???汾??   ??????
  1??
****************************************************************************/
NN_DIGIT subdigitmult(NN_DIGIT *a, NN_DIGIT *b, NN_DIGIT c, NN_DIGIT *d, NN_DIGIT digits)
{
    NN_DIGIT borrow, thigh, tlow;
    NN_DIGIT i;
 
    borrow = 0;
 
    if(c != 0)
    {
        for(i = 0; i < digits; i++)
        {
            dmult(c, d[i], &thigh, &tlow);
            if((a[i] = b[i] - borrow) > (MAX_NN_DIGIT - borrow))
                borrow = 1;
            else
                borrow = 0;
            if((a[i] -= tlow) > (MAX_NN_DIGIT - tlow))
                borrow++;
            borrow += thigh;
        }
    }
    return (borrow);
}
 
/* Decodes character string b into a, where character string is ordered
   from most to least significant.
 
   Lengths: a[digits], b[len].
   Assumes b[i] = 0 for i < len - digits * NN_DIGIT_LEN. (Otherwise most
   significant bytes are truncated.)
 */
void NN_Decode (NN_DIGIT *a, uint32_t digits, uint8_t *b, uint32_t len)
{
    NN_DIGIT t;
    int32_t j;
    uint32_t i, u;
 
    for (i = 0, j = len - 1; i < digits && j >= 0; i++)
    {
        t = 0;
        for (u = 0; j >= 0 && u < NN_DIGIT_BITS; j--, u += 8)
        {
            t |= ((NN_DIGIT)b[j]) << u;
        }
        a[i] = t;
    }
 
    for (; i < digits; i++)
        a[i] = 0;
}
 
/* Encodes b into character string a, where character string is ordered
   from most to least significant.
 
   Lengths: a[len], b[digits].
   Assumes NN_Bits (b, digits) <= 8 * len. (Otherwise most significant
   digits are truncated.)
 */
void NN_Encode (uint8_t *a, uint32_t len, NN_DIGIT *b, uint32_t digits)
{
    NN_DIGIT t;
    int32_t j;
    uint32_t i, u;
 
    for (i = 0, j = len - 1; i < digits && j >= 0; i++)
    {
        t = b[i];
        for (u = 0; j >= 0 && u < NN_DIGIT_BITS; j--, u += 8)
            a[j] = (uint8_t)(t >> u);
    }
 
    for (; j >= 0; j--)
        a[j] = 0;
}
 
/* Assigns a = b.
 
   Lengths: a[digits], b[digits].
 */
void NN_Assign (NN_DIGIT *a, NN_DIGIT *b, uint32_t digits)
{
    if(digits)
    {
        do
        {
            *a++ = *b++;
        }while(--digits);
    }
}
 
/* Assigns a = 0.
 
   Lengths: a[digits].
 */
void NN_AssignZero (NN_DIGIT *a, uint32_t digits)
{
    if(digits)
    {
        do
        {
            *a++ = 0;
        }while(--digits);
    }
}
 
/* Returns the significant length of a in bits, where a is a digit.
 */
static uint32_t NN_DigitBits (NN_DIGIT a)
{
    uint32_t i;
 
    for (i = 0; i < NN_DIGIT_BITS; i++, a >>= 1)
    {
        if (a == 0)
            break;
    }
 
    return (i);
}
 
/* Returns the significant length of a in digits.
 
   Lengths: a[digits].
 */
uint32_t NN_Digits (NN_DIGIT *a, uint32_t digits)
{
    int32_t i;
 
    for (i = digits - 1; i >= 0; i--)
    {
        if (a[i])
            break;
    }
 
    return (i + 1);
}
 
/* Returns sign of a - b.
   Lengths: a[digits], b[digits].
 */
int32_t NN_Cmp (NN_DIGIT *a, NN_DIGIT *b, uint32_t digits)
{
    int32_t i;
 
    for (i = digits - 1; i >= 0; i--)
    {
        if (a[i] > b[i])
            return (1);
        if (a[i] < b[i])
            return (-1);
    }
 
    return (0);
}
 
/* Computes a = b + c. Returns carry.
 
   Lengths: a[digits], b[digits], c[digits].
 */
NN_DIGIT NN_Add (NN_DIGIT *a, NN_DIGIT *b, NN_DIGIT *c, uint32_t digits)
{
    NN_DIGIT ai, carry;
    uint32_t i;
 
    carry = 0;
 
    for (i = 0; i < digits; i++)
    {
        if ((ai = b[i] + carry) < carry)
            ai = c[i];
        else if ((ai += c[i]) < c[i])
            carry = 1;
        else
            carry = 0;
        a[i] = ai;
    }
 
    return (carry);
}
 
 
/* Computes a = b - c. Returns borrow.
 
   Lengths: a[digits], b[digits], c[digits].
 */
NN_DIGIT NN_Sub (NN_DIGIT *a, NN_DIGIT *b, NN_DIGIT *c, uint32_t digits)
{
    NN_DIGIT ai, borrow;
    uint32_t i;
 
    borrow = 0;
 
    for (i = 0; i < digits; i++)
    {
        if ((ai = b[i] - borrow) > (MAX_NN_DIGIT - borrow))
            ai = MAX_NN_DIGIT - c[i];
        else if ((ai -= c[i]) > (MAX_NN_DIGIT - c[i]))
            borrow = 1;
        else
            borrow = 0;
        a[i] = ai;
    }
 
    return (borrow);
}
 
/* Computes a = b * 2^c (i.e., shifts left c bits), returning carry.
 
   Lengths: a[digits], b[digits].
   Requires c < NN_DIGIT_BITS.
 */
NN_DIGIT NN_LShift (NN_DIGIT *a, NN_DIGIT *b, uint32_t c, uint32_t digits)
{
    NN_DIGIT bi, carry;
    uint32_t i, t;
 
    if (c >= NN_DIGIT_BITS)
        return (0);
 
    t = NN_DIGIT_BITS - c;
 
    carry = 0;
 
    for (i = 0; i < digits; i++)
    {
        bi = b[i];
        a[i] = (bi << c) | carry;
        carry = c ? (bi >> t) : 0;
    }
 
    return (carry);
}
 
/* Computes a = c div 2^c (i.e., shifts right c bits), returning carry.
 
   Lengths: a[digits], b[digits].
   Requires: c < NN_DIGIT_BITS.
 */
NN_DIGIT NN_RShift (NN_DIGIT *a, NN_DIGIT *b, uint32_t c, uint32_t digits)
{
    NN_DIGIT bi, carry;
    int32_t i;
    uint32_t t;
 
    if (c >= NN_DIGIT_BITS)
        return (0);
 
    t = NN_DIGIT_BITS - c;
 
    carry = 0;
 
    for (i = digits - 1; i >= 0; i--)
    {
        bi = b[i];
        a[i] = (bi >> c) | carry;
        carry = c ? (bi << t) : 0;
    }
 
    return (carry);
}
 
 
/* Computes a = b * c.
 
   Lengths: a[2*digits], b[digits], c[digits].
   Assumes digits < MAX_NN_DIGITS.
 */
void NN_Mult (NN_DIGIT *a, NN_DIGIT *b, NN_DIGIT *c, uint32_t digits)
{
    NN_DIGIT dhigh, dlow, carry;
    NN_DIGIT bDigits, cDigits, i, j;
    NN_DIGIT mt[2*MAX_NN_DIGITS];
 
    NN_AssignZero (mt, 2 * digits);
 
    bDigits = NN_Digits (b, digits);
    cDigits = NN_Digits (c, digits);
 
    for (i = 0; i < bDigits; i++)
    {
        carry = 0;
        if(*(b+i) != 0)
        {
            for(j = 0; j < cDigits; j++)
            {              
                dmult(*(b+i), *(c+j), &dhigh, &dlow);              
                if((*(mt+(i+j)) = *(mt+(i+j)) + carry) < carry)
                    carry = 1;
                else
                    carry = 0;
                if((*(mt+(i+j)) += dlow) < dlow)
                    carry++;
                carry += dhigh;
            }
        }
        *(mt+(i+cDigits)) += carry;
    }
     
    NN_Assign (a, mt, 2 * digits); 
 
    /* Zeroize potentially sensitive information.
    */
    memset ((uint8_t *)mt, 0, sizeof (mt));
}
 
/* Computes a = c div d and b = c mod d.
 
   Lengths: a[cDigits], b[dDigits], c[cDigits], d[dDigits].
   Assumes d > 0, cDigits < 2 * MAX_NN_DIGITS,
           dDigits < MAX_NN_DIGITS.
 */
void NN_Div (NN_DIGIT *a, NN_DIGIT *b, NN_DIGIT *c, uint32_t cDigits, NN_DIGIT *d, uint32_t dDigits)
{
    NN_DIGIT ai;
    int32_t i;
    uint32_t ddDigits, shift;
    NN_DIGIT div_cc[2*MAX_NN_DIGITS+1], div_dd[MAX_NN_DIGITS]; // ?????????м????
 
    NN_DIGIT s;
    NN_DIGIT t[2], u, v, *ccptr;
    NN_HALF_DIGIT aHigh, aLow, cHigh, cLow;
 
    ddDigits = NN_Digits (d, dDigits);
    if (ddDigits == 0)
        return;
 
    /* Normalize operands.
    */
    shift = NN_DIGIT_BITS - NN_DigitBits (d[ddDigits-1]);
    NN_AssignZero (div_cc, ddDigits);
    div_cc[cDigits] = NN_LShift (div_cc, c, shift, cDigits);
    NN_LShift (div_dd, d, shift, ddDigits);
 
    s = div_dd[ddDigits-1];
 
    NN_AssignZero (a, cDigits);
 
    for (i = cDigits-ddDigits; i >= 0; i--)
    {
        if (s == MAX_NN_DIGIT)
        {
            ai = div_cc[i+ddDigits];
        }
        else
        {
            ccptr = &div_cc[i+ddDigits-1];
 
            s++;
            cHigh = (NN_HALF_DIGIT)HIGH_HALF(s);
            cLow = (NN_HALF_DIGIT)LOW_HALF(s);
 
            *t = *ccptr;
            *(t+1) = *(ccptr+1);
 
            if (cHigh == MAX_NN_HALF_DIGIT)
            {
                aHigh = (NN_HALF_DIGIT)HIGH_HALF(*(t+1));
            }
            else
            {
                aHigh = (NN_HALF_DIGIT)(*(t+1) / (cHigh + 1));
            }
            u = (NN_DIGIT)aHigh * (NN_DIGIT)cLow;
            v = (NN_DIGIT)aHigh * (NN_DIGIT)cHigh;
            if ((*t -= TO_HIGH_HALF(u)) > (MAX_NN_DIGIT - TO_HIGH_HALF(u)))
            {
                t[1]--;
            }
            *(t+1) -= HIGH_HALF(u);
            *(t+1) -= v;
 
            while ((*(t+1) > cHigh) ||   ((*(t+1) == cHigh) && (*t >= TO_HIGH_HALF(cLow))))
            {
                if ((*t -= TO_HIGH_HALF(cLow)) > MAX_NN_DIGIT - TO_HIGH_HALF(cLow))
                    t[1]--;
                *(t+1) -= cHigh;
                aHigh++;
            }
 
            if (cHigh == MAX_NN_HALF_DIGIT)
            {
                aLow = (NN_HALF_DIGIT)LOW_HALF(*(t+1));
            }
            else
            {
                aLow = (NN_HALF_DIGIT)((TO_HIGH_HALF(*(t+1)) + HIGH_HALF(*t)) / (cHigh + 1));
            }
            u = (NN_DIGIT)aLow * (NN_DIGIT)cLow;
            v = (NN_DIGIT)aLow * (NN_DIGIT)cHigh;
            if ((*t -= u) > (MAX_NN_DIGIT - u))
                t[1]--;
            if ((*t -= TO_HIGH_HALF(v)) > (MAX_NN_DIGIT - TO_HIGH_HALF(v)))
                t[1]--;
            *(t+1) -= HIGH_HALF(v);
 
            while ((*(t+1) > 0) || ((*(t+1) == 0) && *t >= s))
            {
                if ((*t -= s) > (MAX_NN_DIGIT - s))
                    t[1]--;
                aLow++;
            }
 
            ai = TO_HIGH_HALF(aHigh) + aLow;
            s--;
        }
 
        div_cc[i+ddDigits] -= subdigitmult(&div_cc[i], &div_cc[i], ai, div_dd, ddDigits);
 
        while (div_cc[i+ddDigits] || (NN_Cmp(&div_cc[i], div_dd, ddDigits) >= 0))
        {
            ai++;
            div_cc[i+ddDigits] -= NN_Sub(&div_cc[i], &div_cc[i], div_dd, ddDigits);
        }
 
        a[i] = ai;
    }
 
    /* Restore result.
    */
    NN_AssignZero (b, dDigits);
    NN_RShift (b, div_cc, shift, ddDigits);
 
    /* Zeroize potentially sensitive information.
    */
    memset ((uint8_t *)div_cc, 0, sizeof (div_cc));
    memset ((uint8_t *)div_dd, 0, sizeof (div_dd));
}
 
/* Computes a = b mod c.
 
   Lengths: a[cDigits], b[bDigits], c[cDigits].
   Assumes c > 0, bDigits < 2 * MAX_NN_DIGITS, cDigits < MAX_NN_DIGITS.
 */
void NN_Mod (NN_DIGIT *a, NN_DIGIT *b, uint32_t bDigits, NN_DIGIT *c, uint32_t cDigits)
{
    NN_DIGIT mod_t[2 * MAX_NN_DIGITS];    // ??????м????
 
    NN_Div (mod_t, a, b, bDigits, c, cDigits);
 
    /* Zeroize potentially sensitive information.
    */
    memset ((uint8_t *)mod_t, 0, sizeof (mod_t));
}
 
/* Computes a = b * c mod d.
 
   Lengths: a[digits], b[digits], c[digits], d[digits].
   Assumes d > 0, digits < MAX_NN_DIGITS.
 */
void NN_ModMult (NN_DIGIT *a, NN_DIGIT *b, NN_DIGIT *c, NN_DIGIT *d, uint32_t digits)
{
    NN_DIGIT mod_t[2 * MAX_NN_DIGITS];    // ??????м????
 
    NN_Mult (mod_t, b, c, digits);
    NN_Mod (a, mod_t, 2 * digits, d, digits);
 
    /* Zeroize potentially sensitive information.
    */
    memset ((uint8_t *)mod_t, 0, sizeof (mod_t));
}
 
/* Computes a = b^c mod d.
 
   Lengths: a[dDigits], b[dDigits], c[cDigits], d[dDigits].
   Assumes d > 0, cDigits > 0, dDigits < MAX_NN_DIGITS.
 */
void NN_ModExp (NN_DIGIT *a, NN_DIGIT *b, NN_DIGIT *c, uint32_t cDigits, NN_DIGIT *d, uint32_t dDigits)
{
    int32_t i;
    uint32_t ciBits, j, s;
    NN_DIGIT ci;
    NN_DIGIT bPower[3][MAX_NN_DIGITS], Exp_t[MAX_NN_DIGITS];   // ????????м????
 
    /* Store b, b^2 mod d, and b^3 mod d.
    */
    NN_Assign (bPower[0], b, dDigits);
    NN_ModMult (bPower[1], bPower[0], b, d, dDigits);
    NN_ModMult (bPower[2], bPower[1], b, d, dDigits);
 
    NN_ASSIGN_DIGIT (Exp_t, 1, dDigits);
 
    cDigits = NN_Digits (c, cDigits);
    for (i = cDigits - 1; i >= 0; i--)
    {
        ci = c[i];
        ciBits = NN_DIGIT_BITS;
 
        /* Scan past leading zero bits of most significant digit.
        */
        if (i == (int)(cDigits - 1))
        {
            while (! DIGIT_2MSB (ci))
            {
                ci <<= 2;
                ciBits -= 2;
            }
        }
 
        for (j = 0; j < ciBits; j += 2, ci <<= 2)
        {
            /* Compute t = t^4 * b^s mod d, where s = two MSB's of ci.
            */
            NN_ModMult (Exp_t, Exp_t, Exp_t, d, dDigits);
            NN_ModMult (Exp_t, Exp_t, Exp_t, d, dDigits);
            if ((s = DIGIT_2MSB (ci)) != 0)
                NN_ModMult (Exp_t, Exp_t, bPower[s-1], d, dDigits);
        }
    }
 
    NN_Assign (a, Exp_t, dDigits);
 
    /* Zeroize potentially sensitive information.
    */
    memset ((uint8_t *)bPower, 0, sizeof (bPower));
    memset ((uint8_t *)Exp_t, 0, sizeof (Exp_t));
}
 
static int32_t RSAPublicBlock (uint8_t *output,                  /* output block */
                                uint32_t *outputLen,              /* length of output block */
                                uint8_t *input,                   /* input block */
                                uint32_t inputLen,                /* length of input block */
                                R_RSA_PUBLIC_KEY *publicKey)    /* RSA public key */
{
    uint32_t eDigits, nDigits;
    NN_DIGIT pc[MAX_NN_DIGITS];           // ???????????????
    NN_DIGIT pe[MAX_NN_DIGITS];           // ??????
    NN_DIGIT pm[MAX_NN_DIGITS];           // ????????
    NN_DIGIT pn[MAX_NN_DIGITS];           // ????
 
    // ??????:??????????????RSA???????????????
    // ???????????????????256????
    NN_Decode (pm, MAX_NN_DIGITS, input, inputLen);
    //NN_Decode (pn, MAX_NN_DIGITS, publicKey->modulus, MAX_RSA_MODULUS_LEN);
    NN_Decode (pn, MAX_NN_DIGITS, publicKey->modulus, publicKey->bits/8);
    NN_Decode (pe, MAX_NN_DIGITS, publicKey->exponent, 4);
    nDigits = NN_Digits (pn, MAX_NN_DIGITS);
    eDigits = NN_Digits (pe, MAX_NN_DIGITS);
 
    if (NN_Cmp (pm, pn, nDigits) >= 0)
        return (RE_DATA);
 
    /* Compute pc = pm^pe mod pn.
    */
    NN_ModExp (pc, pm, pe, eDigits, pn, nDigits);
 
    *outputLen = (publicKey->bits + 7) / 8;
    NN_Encode (output, *outputLen, pc, nDigits);
 
    /* Zeroize sensitive information.
    */
    memset ((uint8_t *)pc, 0, sizeof (pc));
    memset ((uint8_t *)pm, 0, sizeof (pm));
 
    return (0);
}
 
/* Raw RSA private-key operation. Output has same length as modulus.
 
   Assumes inputLen < length of modulus.
   Requires input < modulus.
 */
static int32_t RSAPrivateBlock (uint8_t *output,            /* output block */
                                 uint32_t *outputLen,           /* length of output block */
                                 uint8_t *input,              /* input block */
                                 uint32_t inputLen,             /* length of input block */
                                 R_RSA_PRIVATE_KEY *privateKey)     /* RSA private key */
{
    uint32_t cDigits, nDigits, pDigits, OutLen;
    NN_DIGIT c[MAX_NN_DIGITS];            // ?????????????????????
    NN_DIGIT cP[MAX_NN_DIGITS];           // c?p???????
    NN_DIGIT cQ[MAX_NN_DIGITS];           // c?q???????
    NN_DIGIT dP[MAX_NN_DIGITS];           // ?????p????
    NN_DIGIT dQ[MAX_NN_DIGITS];           // ?????q????
    NN_DIGIT mP[MAX_NN_DIGITS];           // mP = cP^dP mod p
    NN_DIGIT mQ[MAX_NN_DIGITS];           // mQ = cQ^dQ mod q
    NN_DIGIT n[MAX_NN_DIGITS];            // ???
    NN_DIGIT p[MAX_NN_DIGITS];            // ??p????
    NN_DIGIT q[MAX_NN_DIGITS];            // ??q????
    NN_DIGIT qInv[MAX_NN_DIGITS];         // ??p??q????????
    NN_DIGIT t[MAX_NN_DIGITS];            // ??????????????
 
    NN_Decode (c, MAX_NN_DIGITS, input, inputLen);
 
    // ??????:??????????????RSA???????????????
    // ???????????????????256????
    /*NN_Decode(n, MAX_NN_DIGITS, privateKey->modulus, MAX_RSA_MODULUS_LEN);
    NN_Decode(p, MAX_NN_DIGITS, privateKey->prime[0], MAX_RSA_PRIME_LEN);
    NN_Decode(q, MAX_NN_DIGITS, privateKey->prime[1], MAX_RSA_PRIME_LEN);
    NN_Decode(dP, MAX_NN_DIGITS, privateKey->primeExponent[0], MAX_RSA_PRIME_LEN);
    NN_Decode(dQ, MAX_NN_DIGITS, privateKey->primeExponent[1], MAX_RSA_PRIME_LEN);
    NN_Decode(qInv, MAX_NN_DIGITS, privateKey->coefficient, MAX_RSA_PRIME_LEN);*/
 
    NN_Decode(n, MAX_NN_DIGITS, privateKey->modulus, privateKey->bits/8);
    NN_Decode(p, MAX_NN_DIGITS, privateKey->prime[0], privateKey->bits/16);
    NN_Decode(q, MAX_NN_DIGITS, privateKey->prime[1], privateKey->bits/16);
    NN_Decode(dP, MAX_NN_DIGITS, privateKey->primeExponent[0], privateKey->bits/16);
    NN_Decode(dQ, MAX_NN_DIGITS, privateKey->primeExponent[1], privateKey->bits/16);
    NN_Decode(qInv, MAX_NN_DIGITS, privateKey->coefficient, privateKey->bits/16);
 
    cDigits = NN_Digits (c, MAX_NN_DIGITS);
    nDigits = NN_Digits (n, MAX_NN_DIGITS);
    pDigits = NN_Digits (p, MAX_NN_DIGITS);
 
    if (NN_Cmp (c, n, nDigits) >= 0)
        return (RE_DATA);
 
    /* Compute mP = cP^dP mod p  and  mQ = cQ^dQ mod q. (Assumes q has
    length at most pDigits, i.e., p > q.)
    */
    NN_Mod (cP, c, cDigits, p, pDigits);
    NN_Mod (cQ, c, cDigits, q, pDigits);
    NN_ModExp (mP, cP, dP, pDigits, p, pDigits);
    NN_AssignZero (mQ, nDigits);
    NN_ModExp (mQ, cQ, dQ, pDigits, q, pDigits);
 
    /* Chinese Remainder Theorem:
    m = ((((mP - mQ) mod p) * qInv) mod p) * q + mQ.
    */
    if (NN_Cmp (mP, mQ, pDigits) >= 0)
        NN_Sub (t, mP, mQ, pDigits);
    else
    {
        NN_Sub (t, mQ, mP, pDigits);
        NN_Sub (t, p, t, pDigits);
    }
    NN_ModMult (t, t, qInv, p, pDigits);
    NN_Mult (t, t, q, pDigits);
    NN_Add (t, t, mQ, nDigits);
 
    OutLen = (privateKey->bits + 7) / 8;
    if(outputLen != NULL)
    {
        *outputLen = OutLen;
    }
    if(output != NULL)
    {
        NN_Encode (output, OutLen, t, nDigits);
    }
 
    /* Zeroize sensitive information.
    */
    memset ((uint8_t *)c, 0, sizeof (c));
    memset ((uint8_t *)cP, 0, sizeof (cP));
    memset ((uint8_t *)cQ, 0, sizeof (cQ));
    memset ((uint8_t *)dP, 0, sizeof (dP));
    memset ((uint8_t *)dQ, 0, sizeof (dQ));
    memset ((uint8_t *)mP, 0, sizeof (mP));
    memset ((uint8_t *)mQ, 0, sizeof (mQ));
    memset ((uint8_t *)p, 0, sizeof (p));
    memset ((uint8_t *)q, 0, sizeof (q));
    memset ((uint8_t *)qInv, 0, sizeof (qInv));
    memset ((uint8_t *)t, 0, sizeof (t));
 
    return (0);
}
 
 
int  rsa_public(void *outbuf, int *outlen, const void *inbuf, int inlen, const R_RSA_PUBLIC_KEY *pubkey)
{
    int status;
    uint32_t modulusLen, pkcsBlockLen=0;
    uint8_t pkcsBlock[MAX_RSA_MODULUS_LEN]; // ????????????????????????
 
    if((outbuf == NULL) || (pubkey == NULL)) {
        return(-1);
    }
    modulusLen = (pubkey->bits + 7) / 8;
    if (inlen > modulusLen){
        return (RE_LEN);
    }
 
    status = RSAPublicBlock(pkcsBlock, &pkcsBlockLen, (uint8_t *)inbuf, inlen, (R_RSA_PUBLIC_KEY *)pubkey);
    if(status){
        return (status);
    }
 
    if(pkcsBlockLen != modulusLen){
        return (RE_LEN);
    }
     
    if(outlen != NULL){
        *outlen = modulusLen;
    }
 
    if(outbuf != NULL){
        memcpy(outbuf, pkcsBlock, modulusLen);
    }
 
    /* Zeroize potentially sensitive information.
    */
    memset(pkcsBlock, 0, sizeof (pkcsBlock));
 
    return (0);
}
 
 
int  rsa_private(void *outbuf, int *outlen, const void *inbuf, int inlen, const R_RSA_PRIVATE_KEY *prikey)
{
    int status;
    uint32_t i, modulusLen;
    uint8_t pkcsBlock[MAX_RSA_MODULUS_LEN]; // ??????????????????????
 
    if((inbuf == NULL) || (prikey == NULL)){
        return(-1);
    }
    modulusLen = (prikey->bits + 7) / 8;
 
    if (inlen  > modulusLen){
        return (RE_LEN);
    }
 
    i = 0;
    memcpy (pkcsBlock+i, inbuf, inlen);
 
    *outlen = 0;
    status = RSAPrivateBlock((uint8_t*)outbuf, (uint32_t *)outlen, pkcsBlock, modulusLen, (R_RSA_PRIVATE_KEY *)prikey);
 
    /* Zeroize potentially sensitive information.
    */
    memset (pkcsBlock, 0, sizeof (pkcsBlock));
 
    return (status);
}