【周志华机器学习】机器学习中的距离度量
文章目录
- 参考资料
- 1. 欧氏距离
- 2. 曼哈顿距离
- 3. 切比雪夫距离
- 4. 闵可夫斯基距离
- 5. 标准化欧氏距离
- 6. 马氏距离
- 7. 巴氏距离
- 8. 汉明距离
- 9. 夹角余弦
- 10. 杰卡德相似系数
- 11. 皮尔逊系数
参考资料
- ML-NLP
- 机器学习各种距离优缺点
- 常见距离度量方法优缺点对比
K近邻算法的核心在于找到实例点的邻居,这个时候,问题就接踵而至了,如何找到邻居,邻居的判定标准是什么,用什么来度量。这一系列问题便是下面要讲的距离度量表示法。
1. 欧氏距离
欧氏距离,最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于欧几里得空间中,如点 x = (x1,…,xn) 和 y = (y1,…,yn) 之间的距离为:
![]()
-
二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离:

-
三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:

-
两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离:

也可以用表示成向量运算的形式:

缺点:
虽然这是一种常见的距离测量方法,但欧几里得距离并不是尺度不变的,这意味着计算出的距离可能会根据特征的单位而有所偏斜。通常情况下,在使用这种距离测量之前,需要对数据进行归一化。
此外,随着数据维度的增加,欧几里得距离的作用就越小。这与维度的诅咒有关,它涉及到高维空间的概念,并不像我们直观地期望的那样,从二维或三维空间中发挥作用。
用例
当你有低维数据,并且向量的大小很重要,需要测量时,欧氏距离的效果非常好。如果在低维数据上使用欧氏距离,kNN和HDBSCAN等方法就会显示出很好的效果。
虽然已经开发了许多其他的测量方法来解释欧氏距离的缺点,但它仍然是最常用的距离测量方法之一,这是有充分理由的。它使用起来非常直观,实现起来也很简单,并且在许多用例中都显示出了很好的效果。
2. 曼哈顿距离
曼哈顿距离,我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离,也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上,坐标(x1, y1)的点P1与坐标(x2, y2)的点P2的曼哈顿距离为: ∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ |x_1-x_2|+|y_1-y_2| ∣x1−x2∣+∣y1−y2∣,要注意的是,曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。
通俗来讲,想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。而实际驾驶距离就是这个“曼哈顿距离”,此即曼哈顿距离名称的来源, 同时,曼哈顿距离也称为城市街区距离(City Block distance)。
-
二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离

-
两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离

优点:
曼哈顿距离中的距离计算公式比欧氏距离的计算公式看起来简洁很多,只需要把两个点坐标的 x 坐标相减取绝对值,y 坐标相减取绝对值,再加和。
从公式定义上看,曼哈顿距离一定是一个非负数,距离最小的情况就是两个点重合,距离为 0,这一点和欧氏距离一样。
曼哈顿距离和欧氏距离的意义相近,也是为了描述两个点之间的距离,不同的是曼哈顿距离只需要做加减法,这使得计算机在大量的计算过程中代价更低,而且会消除在开平方过程中取近似值而带来的误差。不仅如此,曼哈顿距离在人脱离计算机做计算的时候也会很方便。
缺点
虽然曼哈顿距离对于高维数据似乎还不错,但它是一个比欧几里得距离更不直观的测量方法,尤其是在高维数据中使用时。
而且,它比欧几里得距离更容易给出一个更高的距离值,因为它不可能是最短路径。这不一定会带来问题,但你应该考虑到这一点。
3. 切比雪夫距离
切比雪夫距离,若二个向量或二个点p 、and q,其座标分别为Pi及qi,则两者之间的切比雪夫距离定义如下:
![]()
这也等于以下Lp度量的极值: ![]() ,因此切比雪夫距离也称为L∞度量。
,因此切比雪夫距离也称为L∞度量。
以数学的观点来看,切比雪夫距离是由一致范数(uniform norm)(或称为上确界范数)所衍生的度量,也是超凸度量(injective metric space)的一种。
在平面几何中,若二点p及q的直角坐标系坐标为(x1,y1)及(x2,y2),则切比雪夫距离为:
![]()
玩过国际象棋的朋友或许知道,国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?。你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步 。有一种类似的一种距离度量方法叫切比雪夫距离。
-
二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离 :

-
两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的切比雪夫距离:

这个公式的另一种等价形式是
d 12 = l i m k → ∞ ( ∑ i = 1 n ∣ x 1 i − x 2 i ∣ k ) 1 / k ) d_{12}=lim_{k\to\infin}(\sum_{i=1}^{n}|x_{1i}-x_{2i}|^k)^{1/k}) d12=limk→∞(i=1∑n∣x1i−x2i∣k)1/k)
切比雪夫距离可以用来提取从一个方格到另一个方格所需的最少步数。此外,在允许无限制的8向移动的棋局中,它也是一个有用的测量方法。
在实践中,切比雪夫距离经常被用于仓库物流
4. 闵可夫斯基距离
闵可夫斯基距离(Minkowski Distance),闵氏距离不是一种距离,而是一组距离的定义。
两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的闵可夫斯基距离定义为:
![]()
其中p是一个变参数。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
根据变参数的不同,闵氏距离可以表示一类的距离。
5. 标准化欧氏距离
标准化欧氏距离,标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路:既然数据各维分量的分布不一样,那先将各个分量都“标准化”到均值、方差相等。至于均值和方差标准化到多少,先复习点统计学知识。
假设样本集X的数学期望或均值(mean)为m,标准差(standard deviation,方差开根)为s,那么X的“标准化变量”X*表示为:(X-m)/s,而且标准化变量的数学期望为0,方差为1。
即,样本集的标准化过程(standardization)用公式描述就是:
![]()
标准化后的值 = ( 标准化前的值 - 分量的均值 ) /分量的标准差
经过简单的推导就可以得到两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的标准化欧氏距离的公式:
6. 马氏距离
有M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到u的马氏距离表示为:
![]()
-
若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式就成了,也就是欧氏距离了:

-
若协方差矩阵是对角矩阵,公式变成了标准化欧氏距离。
马氏距离的优缺点:量纲无关,排除变量之间的相关性的干扰。
7. 巴氏距离
在统计中,巴氏距离距离测量两个离散或连续概率分布的相似性。它与衡量两个统计样品或种群之间的重叠量的巴氏距离系数密切相关。巴氏距离距离和巴氏距离系数以20世纪30年代曾在印度统计研究所工作的一个统计学家A. Bhattacharya命名。同时,Bhattacharyya系数可以被用来确定两个样本被认为相对接近的,它是用来测量中的类分类的可分离性。
对于离散概率分布 p和q在同一域 X,它被定义为:
![]()
其中:
![]()
是Bhattacharyya系数。
8. 汉明距离
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。应用:信息编码(为了增强容错性,应使得编码间的最小汉明距离尽可能大)。
缺点
正如你所预料的,当两个向量的长度不相等时,汉明距离很难使用。你会希望将相同长度的向量相互比较,以了解哪些位置不匹配。
而且,只要它们不同或相等,它就不考虑实际值。因此,当幅度是一个重要的衡量标准时,不建议使用这个距离衡量。
用例
典型的使用情况包括在计算机网络上传输数据时的纠错/检测。它可以用来确定二进制字中的失真位数,以此来估计错误。
此外,你还可以使用汉明距离来测量分类变量之间的距离。
9. 夹角余弦
几何中夹角余弦可用来衡量两个向量方向的差异,机器学习中借用这一概念来衡量样本向量之间的差异。
-
在二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式:

-
两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦:
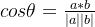
夹角余弦取值范围为[-1,1]。夹角余弦越大表示两个向量的夹角越小,夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1,当两个向量的方向完全相反夹角余弦取最小值-1。
缺点
余弦相似性的一个主要缺点是不考虑向量的大小,只考虑其方向。在实际应用中,这意味着值的差异没有被完全考虑。以推荐系统为例,那么余弦相似性并没有考虑到不同用户之间的评分等级差异。
用例
当我们有高维数据且向量的大小并不重要时,我们经常使用余弦相似度。对于文本分析来说,当数据用字数来表示时,这种测量方法是很常用的。
例如,当一个词在一个文档中出现的频率高于另一个文档时,这并不一定意味着一个文档与该词的关系更大。可能是文档的长度不均匀,计数的大小就不那么重要了。那么,我们最好是使用不考虑大小的余弦相似性。
10. 杰卡德相似系数
两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示。杰卡德相似系数是衡量两个集合的相似度一种指标。
![]()
与杰卡德相似系数相反的概念是杰卡德距离:
![]()
11. 皮尔逊系数
在统计学中,皮尔逊积矩相关系数用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。通常情况下通过以下取值范围判断变量的相关强度:
0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关
简单说来,各种“距离”的应用场景简单概括为,
- 空间:欧氏距离,
- 路径:曼哈顿距离,国际象棋国王:切比雪夫距离,
- 以上三种的统一形式:闵可夫斯基距离,
- 加权:标准化欧氏距离,
- 排除量纲和依存:马氏距离,
- 向量差距:夹角余弦,
- 编码差别:汉明距离,
- 集合近似度:杰卡德类似系数与距离,
- 相关:相关系数与相关距离。