《强化学习Sutton》读书笔记（一）——多臂赌博机（Multi-armed Bandits）

此为《强化学习》第二章。

多臂赌博机问题描述

问题描述略。理想状态下，如果我们可以知道做出行为 a a 时得到的期望价值，那问题就结了，按期望选择最大的就好了。它的表达式为：

q∗(a)≐E[Rt|At=a] q ∗ ( a ) ≐ E [ R t | A t = a ]

其中，选择行为 a a 的理论期望价值q∗(a) q ∗ ( a ) 定义为在第 t t 步选择行为 (Action) a a 得到的奖励 (Reward) Rt R t 的期望。

但显然，我们是不可能精确得到 q∗(a) q ∗ ( a ) 的，所以我们用 Qt(a) Q t ( a ) 作为第 t t 步选择行为a a 对价值进行估计，希望 Qt(a) Q t ( a ) 可以逼近 q∗(a) q ∗ ( a ) 。

采样方法

第一种方法是基于采样得到采样平均 (Sample Average) 。采样平均就是统计每次选择行为 a a 得到奖励的平均值，即

Qt(a)≐∑t−1i=1RiIAi=a∑t−1i=1IAi=a Q t ( a ) ≐ ∑ i = 1 t − 1 R i I A i = a ∑ i = 1 t − 1 I A i = a

其中 I I 表示指示函数。

如果采用贪心法，则采样方法下的策略为

At=argmaxaQt(a) A t = arg ⁡ max a Q t ( a )

完全的贪心只能保证选择了当前最优解，并不能保证其他未被完全探索到的行为不会产生更大的奖励。考虑到对开发 (Exploit) 和探索 (Explore) 之间的平衡，也常使用 ϵ ϵ -贪心法。

10臂赌博机的例子

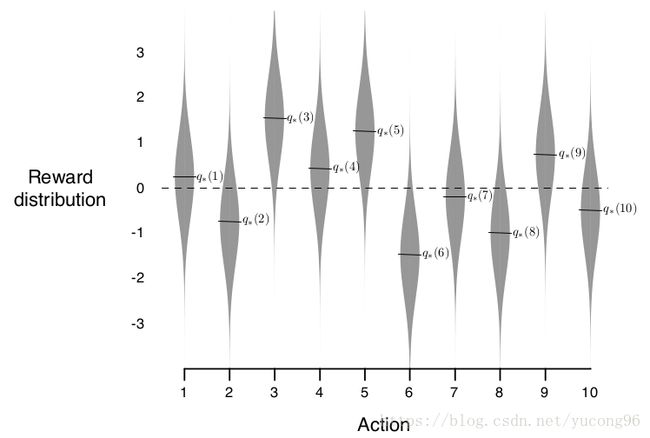
假如有一个奖励分布如下图所示的多臂赌博机，

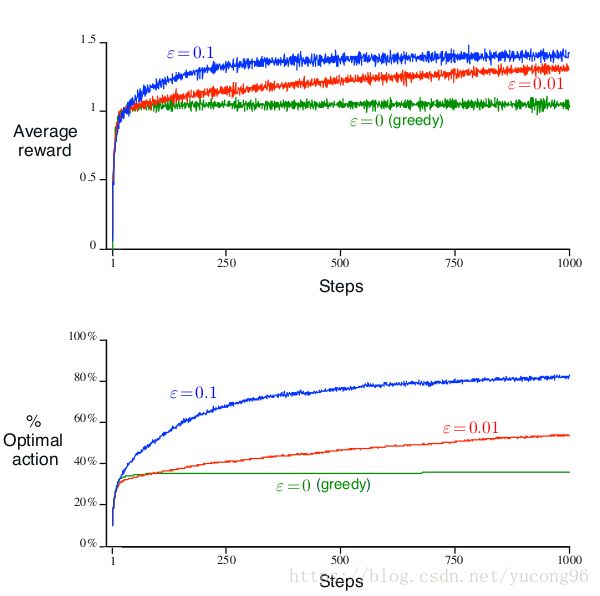
使用不同的 ϵ ϵ 的贪心算法得到的结果不同，它也反应了探索的重要性。

增量式实现

在采样方法一节中， Qt(a) Q t ( a ) 表示为一组奖励的求平均，非常直观，但要求存下每一步的奖励，对空间开销较大。对 Qt(a) Q t ( a ) 稍作移项，就可以得到它的迭代式更新方法。（以下表达式省略 a a ，均表示a a 下的价值估计和奖励）

Qn+1=1n∑i=1nRi=1n(Rn+(n−1)Qn)=Qn+1n(Rn−Qn) Q n + 1 = 1 n ∑ i = 1 n R i = 1 n ( R n + ( n − 1 ) Q n ) = Q n + 1 n ( R n − Q n )

变化奖励下的多臂赌博机

在上述的方法下，我们都假定了多臂赌博机的奖励符合一个固定的分布，与时间无关。如果与时间相关呢？我们可能更希望较近的采样比以前的采样具有更高的权重。我们对上一节的 Qn+1 Q n + 1 进行微调

Qn+1=Qn+α(Rn−Qn) Q n + 1 = Q n + α ( R n − Q n )

与之前的 1/n 1 / n 不同，此时 α α 为一个 [0,1) [ 0 , 1 ) 的常数。不难得到，

Qn+1=(1−α)nQ1+∑i=1nα(1−α)n−iRi Q n + 1 = ( 1 − α ) n Q 1 + ∑ i = 1 n α ( 1 − α ) n − i R i

可以看出， i i 越小，Ri R i 的权重越低。 α α 除了可以设置为常数外，也可以是和 n n 相关的函数，比如上一节中的1/n 1 / n 。不过这样就需要自己判断不同时间奖励的权重关系了。

初值设定

增量式地更新价值估计，有一个和采样方法不同的地方，即 Q1(a) Q 1 ( a ) 的出现，它使我们的估计是有偏的（虽然偏差会随着时间增加而降低，趋向于0）。但这种偏差有时可以被我们利用，比如可以加入我们的先验知识。再比如，过于乐观（过大）的 Q1(a) Q 1 ( a ) 能够激励探索，因为每次行为总是在降低行为 a a 的期望，从而鼓励探索其他行为。下图在上述的10臂赌博机例子上实验了乐观估计和保守估计的不同。

上限置信边界行为选择

上限置信边界 (Upper-Confidence-Bound) 是个奇怪的名字。不过它的思路是清晰的。在ϵ ϵ -贪心下， ϵ ϵ 是一个经验性的常数，而我们常常会希望在学习开始初期多进行探索，而后期比较明确各行为的奖励时则多进行开发，一个简单的常数 ϵ ϵ 是不够的。

UCB的策略是这样的

At=argmaxa[Qt(a)+clntNt(a)−−−−−√] A t = arg ⁡ max a [ Q t ( a ) + c ln ⁡ t N t ( a ) ]

当总采样次数 t t 增大，而行为a a 被采样的次数 Nt(a) N t ( a ) 不变，式子第二项就会逐渐增大，使探索总是能够发生。 c c 可以用来调节开发和探索的比例。

下图表现了UCB和ϵ ϵ -贪心的对比。

梯度赌博机算法

在之前的例子中，我们总是采取了贪心的算法（包括 ϵ ϵ -贪心）作为策略。贪心算法突出了当前最优的一个行为，而将其他行为几乎视为等价。本节中，我们按照概率来选择行为。我们把策略记为 πt(a) π t ( a ) ，表示在第 t t 步选择行为a a 的概率。概率具体的值是它们偏好的softmax，即

πt(a)≐Pr{At=a}≐eHt(a)∑kb=1eHt(b) π t ( a ) ≐ Pr { A t = a } ≐ e H t ( a ) ∑ b = 1 k e H t ( b )

其中， k k 表示赌博机的数量，Ht(a) H t ( a ) 表示对行为 a a 的偏好 (Perference) ，Ht(a) H t ( a ) 表达式为

(a=At):Ht+1(a)=Ht(a)+α(Rt−R¯t)(1−πt(a))(a≠At):Ht+1(a)=Ht(a)−α(Rt−R¯t)πt(a) ( a = A t ) : H t + 1 ( a ) = H t ( a ) + α ( R t − R ¯ t ) ( 1 − π t ( a ) ) ( a ≠ A t ) : H t + 1 ( a ) = H t ( a ) − α ( R t − R ¯ t ) π t ( a )

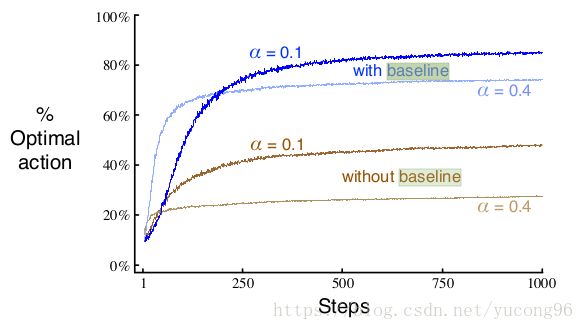
其中， R¯t R ¯ t 表示 t t 步时的平均奖励，它将作为衡量奖励大小的参考 (Baseline) 。显然，如果Rt>R¯t R t > R ¯ t ，那么 Ht+1(At) H t + 1 ( A t ) 将增大，而其他行为的偏好将减小。而所有偏好的和将保持不变。下图表现了baseline有无和探索/开发平衡性的不同效果。

上述的公式其实有点无厘头，尤其是和标题中的“梯度”没有任何关系。可以证明（过程详见书本），

Ht+1(a)=Ht(a)+α∂E[Rt]∂Ht(a) H t + 1 ( a ) = H t ( a ) + α ∂ E [ R t ] ∂ H t ( a )

联合搜索（上下文赌博机）

上述的赌博机都是一次性的赌博机——做出一个行为后立刻得到回报，且下一次仍然面对同样的赌博机。但实际问题很可能需要一组策略而非单个策略。这将在以后的章节中讨论。

参考文献

《Reinforcement Learning: An Introduction (second edition)》Richard S. Sutton and Andrew G. Barto

上一篇：无
下一篇：《强化学习Sutton》读书笔记（二）——有限马尔科夫决策过程（Finite Markov Decision Processes）