趣味三角——第5章——苍穹和地球的测量

                                      

目录

5.1. 三角学在测量天体和地球的应用中发展

5.2. Abraham De Moivre在天体和地球测量中的数学贡献

---

第5章   天体和地球的测量

5.1. 三角学在测量苍穹和地球的应用中发展

The science of trigonometry was in a sense a precursor

of the telescope. It brought faraway objects within the

compass of measurement and first made it possible

for man to penetrate in a quantitative manner the far

reaches of space

(在某种意义上，三角学科学是望远镜技术的先驱。它将遥远的天体带到了人类可测的范围内，第一次使人类以量化方式洞悉太空远处成为可能。)

——Stanley L. Jaki, <> (物理学的相关性)(1966年)

    几何从其最早的时候起，就被应用于实际的测量问题——无论是计算金字塔的高度、田地的面积，还是地球的大小。事实上，“几何(geometry)”这个词源自希腊语“geo”(地球)和“metron”(测量)。但早期希腊科学家的野心甚至更远：他们试图使用简单的几何学和后来的三角学来估计宇宙的大小。

萨摩斯岛的(Samos)阿里斯塔克斯(Aristarchus)(约公元前310-230年)被认为是历史上第一位伟大的天文学家。尽管他的大多数前辈都是根据美学和神话原则得出他们的宇宙图景，但Aristarchus的结论完全基于他可用的观测数据。例如，他指出，如果我们假设太阳而不是地球处于宇宙的中心，那么行星(planets)的运动就可以得到最好的解释——这比哥白尼提出他的日心系统早了将近2000 年。[1] Aristarchus的大部分著作都遗失了，但一部关于太阳和月亮的大小和距离的数学天文学论文幸存下来。在其中，他开发了一种几何方法来确定太阳和月亮与地球的距离之比。

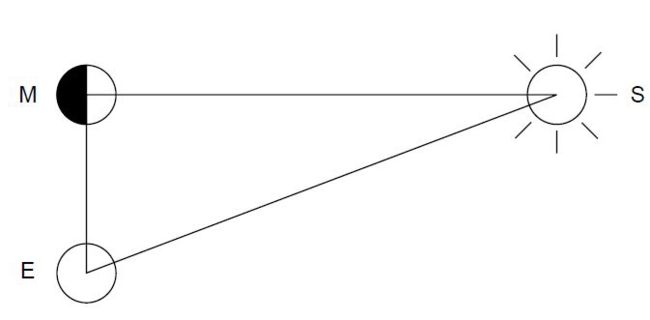
他的方法被称为“月球二分法(lunar dichotomy)”(来自希腊语dichotomos，分为两部分)，基于这样一个事实，即在月球圆盘的一半似乎恰好被太阳照亮的那一刻，就像在每个月球周期上发生两次一样，从地球到月球以及从月球到太阳的视线形成一个直角(图 22)。它遵从这样的原理，即，假如我们已知角EMS，在原理上，我们可以求得三角形EMS的边的比率，特别是求得ES/EM的比率。Aristarchus认为，∠MES是“从一个象限的三十分之一到一个象限边界处的角，” 即，∠MES = 90°- 30°= 87°。根据现代三角学知识，则可以推理出，ES/EM = sec 87°= 19.1 。当然，Aristarchus在处理这个问题的时候，还没有三角表，因此，他必须依懒一个定理，即，用现代数学符号来说，就是：如果α和β是两个锐角，则sin(α)/ sin(β) < α/β < tan(α)/tan(β)。[2] 据此，他推断出，ES/EM大于18：1小于20：1。

----------------------图22 Aristarchus的方法----------------------------------

现在这个 ES/EM 比率的估算值远低于实际值，实际值约为390。原因是Aristarchus的方法虽然在原则上是合理的，但实施起来却非常不切实际。一方面，即使使用现代望远镜，也很难确定二分法的确切时刻；其次，测量角度MES 也同样困难——必须直视太阳，而太阳可能在二分法的瞬间已经落山(set)。此外，因为∠MES非常接近90°, 其判定中的一个小错误会导致比率ES/EM的大错误。例如，假如∠MES昌88°而不是87°, ES/EM会是28.7，而对于86°, 它会是14.3。然而，Aristarchus的方法标志着首次尝试根据对可观测量的实际测量来估计我们行星系统的尺寸。

Aristarchus还估计了太阳和月亮的大小比例。在日全食期间，月亮完全覆盖了日盘——但只是勉强覆盖，这就是日全食持续时间如此短的原因——不超过大约七分钟，而且通常要短得多。[3] 这意味着，当从地球上看的时候，太阳和月亮的“表面 (apparent)”尺寸大致相等(在天球上测量大约半度弧度)。因此，这些物体的实际直径之比必须与它们与地球的距离之比几乎相同。 Aristarchus因此得出结论，太阳的直径是月球直径的 18 到 19 倍。 实际比例约为400。

现在估计两个远处物体的距离比是一回事，但估计它们的实际距离和大小则完全是另一回事。视差现象(parallax)在这里起着至关重要的作用。当观察者改变自己的位置，或者当两个观察者在不同的地方同时观察时，一个物体似乎改变了它的位置是一种常见的经验——从远处的背景来看。如果知道两个观察者之间的距离(基线的长度)，那么通过测量物体位置的明显角度偏移(视差角)，就可以使用简单的三角函数计算出到物体的距离。视差法是大地测量的基础，但当将其应用于天体之间的巨大距离时，其准确性是有限的：物体越远，视差角越小，估计距离的不确定性越大。

由于月球离我们相对较近，因此地球上不同位置的两名观察者所看到的明显位置变化，虽然以地球标准(terrestrial standards)来看很小，但在天文尺度上(astronomical scale)却是相当大的。然而，为了使其有任何实际用途，这两个观察者必须尽可能远离对方——最好是在地球上的相对点。然而，在罕见的日全食期间，即使是观察者位置的轻微变化也可能意味着完全黑暗和部分日食之间的差异。 这在1925年1月24日的日食中得到了戏剧性的体现，它正好穿过纽约市，在晴朗的天空中被数百万人观看。为了确定月亮阴影的确切边缘，观察员驻扎在曼哈顿第72街和第135街之间的每个十字路口，并奉命报告他们是否看到了太阳日冕(corona)——只有在全食期间才能看到，此时太阳盘完全被月亮覆盖——或者仅仅是一个狭窄的新月形太阳，表明日食是偏食的。“结果很明确：本影(umbra)的边缘[月亮的影子]通过第 95 街和第97街之间，投射在超过200,000英里距离的阴影的精度可达数百英尺。”[4]

第一个使用月视差来估计月球距离的是尼西亚(Nicaea)的希帕克斯(Hipparchus)，我们已经在第2章中见过他。Hipparchus仔细研究了可追溯到公元前8世纪的古代巴比伦日食记录，并从中获得了对月食的透彻理解。太阳和月亮的运动。幸运的是，就在他出生前几年，在离他的出生地不远的地方发生了一次日食；这次日食最近被确定为公元前189年3月 14日，在赫勒斯滂海峡(Hellespont) (在现代土耳其达达尼尔海峡的直线)附近，而在亚历山大港，只有五分之四的太阳圆盘被月亮遮住。由于在天球上测得太阳和月亮对着大约半度弧度，因此月亮的表面位置偏移量相当于此值的五分之一，即大约6弧分。结合这些信息和两地的经纬度以及月食时太阳和月亮的仰角，Hipparchus能够计算出月亮的最小距离和最大距离分别为地球半径的71倍和83倍。虽然这些估计值超过了56和64的现代值，但它们处于正确的数量级之内，在他那个时代应该被视为一项卓越的成就。[5]

Hipparchus根据地球半径估计了月球的距离。要用更常用的单位来表示这个距离，就必须知道地球的大小。地球是球形的概念是毕达哥拉斯提出的；他是从观测证据(例如，在月偏食期间，地球总是在月球上投下圆形阴影这一事实)或更可能是从美学和哲学原理(球体最完美的所有形状)是未知的。 但是一旦球形地球的概念站稳脚跟，人们就开始尝试确定它的大小。实现这一壮举的功劳归功于公元前2世纪杰出的数学家和地理学家Cyrene的埃拉托色尼(Eratosthenes of Cyrene，约公元前275–194年）。

Eratosthenes是古代最伟大的科学家阿基米德的一个朋友，阿基米德向他介绍了他的几部著作。与早期的大多数学者一样，Eratosthenes活跃于多个学科。他制作了一张包含 675颗恒星的天体图，并确定了赤道(equator)与黄道(ecliptic)(地球绕日轨道平面)的倾角——大约23.5°。他建议每四年在日历中增加一天，以使其与季节保持同步，后来的儒略历就是基于这个想法。在数学方面，他设计了著名的“筛子(sieve)”来寻找质数(prime numbers)，并给出了重复问题的机械解决方案：找到一个立方体的边，该立方体的体积等于给定立方体的两倍。Eratosthenes还写诗和文学评论，并且是第一个对可追溯到特洛伊战争的重大历史事件进行科学编年史的人。 他的朋友给他取了个绰号“Beta”，也许是因为他们认为他仅次于阿基米德；但这种轻视并没有阻止埃及统治者托勒密三世(Ptolemy III)邀请他领导亚历山大港(Alexandria)的大图书馆，这是古代世界最大的学术著作宝库。年老时，他双目失明，意识到自己多产的岁月已经结束，自愿饿死，堪称“哲学家之死(philosopher’s death)”。

在公元前240年。Eratosthenes实现了他主要被人们记住的壮举：计算地球的大小。 众所周知，夏至那天的中午(一年中白昼最长的一天)，太阳的光芒直接照亮了上埃及 Syene(今阿斯旺)镇的一口深井底部；也就是说，那天中午太阳刚好在头顶上方。但在亚历山大港，在Syene正北，那一刻太阳与天顶的距离为整圆的五十分之一(即 7:2)，这是通过垂直杆的阴影测量的(图23)。Eratosthenes 假设太阳离地球很远，以至于它的光线几乎平行地到达我们；因此，从这两个位置看到的太阳高度差一定是由于地球的球形造成的。由于亚历山大港和Syene之间的距离为 5,000 stadia(以国王的使者在两座城市之间奔跑所花费的时间来衡量)，地球的周长必须是该距离的五十倍，即 250,000 stadia。

----------------------图23 Eratosthenes测量地球周长的方法---------------------

遗憾的是，体育场的确切长度，即希腊时代的地理距离单位，无人知晓；估计值从607 英尺到738英尺不等，较小的数字指的是后来使用的罗马体育场。因此，Eratosthenes发现的地球周长在29,000 到 35,000 英里之间，而正确的值是极地周长(polar circumference)为 24,818 英里，赤道周长(equatorial circumference)为24,902 英里。[6] Eratosthenes因此非常接近，在这样做时他使用了字面意义上的几何科学：测量地球。

费迪南德·麦哲伦(Ferdinand Magellan)的历史性环球航行(1519-1522年)首次直接证明了地球大致是球形的。 但此后不久，科学家们开始怀疑它可能真的是平坦的；问题是，它是在两极(扁球体)还是在赤道(长球体)变平？这不仅仅是一个学术问题：随着探索时代的深入，航海者能够足够准确地确定他们在海上的位置——他们的经度和纬度——变得至关重要。这又取决于了解沿子午线(meridian)测量的纬度的长度(“子午度(meridional degree)”)。如果地球是一个完美的球体，无论纬度本身如何，度数在任何地方都具有相同的长度。但如果地球是扁圆的，度数的长度会向两极略微增加，而如果是椭圆形(oblate)，则长度会减少。确定地球的确切形状——更一般地说，确定任何曲面的形状——演变成了大地测量学。18 和 19 世纪一些最伟大的数学家解决了这个问题，其中包括牛顿(Newton)、欧拉(Euler)和高斯(Gauss)。

大地测量的第一步是选择已知长度的基线，然后测量这条线与从其端点到远处地标的视线之间的角度。对于相对较小的区域——一个城镇或一个县——人们可能会忽略地球的曲率并认为该区域是平面的；然后可以使用正弦定律(ASA案例)计算任一端点到地标的距离。 这些距离现在可以用作新的基线并重复该过程，直到整个区域被三角形网络覆盖。这个过程被称为三角测量；它提供了骨架，土地的地形细节——山丘、河流、湖泊、城镇和道路——稍后叠加在一起形成完整的地图。[7]

早在1533年，荷兰数学家Gemma Frisius(1508-1555年)就提出了三角测量法。[8] 另一位荷兰人 Willebrord van Roijen Snell(1581-1626年)首次大规模实施了该方法[9]，他于1615年使用33个三角形的网格调查了荷兰80英里的延伸区域。但正是在法国，1668 年，在巴黎天文台的创始人之一让·皮卡德神甫(Abb´e Jean Picard，1620-1682年)的指导下，进行了第一次全面的、由政府赞助的三角测量工作。作为他的基线，他选择了从巴黎到枫丹白露的7英里路段；从这个基线开始，调查最终将覆盖整个法国。为了提高测量的准确性，皮卡德使用了一种新型象限仪(一种测量垂直角的仪器)，其中一个带有十字线的望远镜取代了两个用于瞄准的针孔。将他的地面测量与天文测量相结合,确定他的基线端点的纬度后，皮卡德得出巴黎纬度的度数为68.65英里。 随后，他将调查范围扩大到法国海岸线，结果出现了一个不受欢迎的发现：该国的西海岸必须相对于穿过巴黎的本初子午线向东偏移, 这让君主路易十四惊呼：“你的旅程已经让我失去了我的大部分领土！”[10]

皮卡德于1682年去世后，卡西尼家族这个杰出的天文学家家族的四代人继续进行了另一个世纪的调查。乔瓦尼·多米尼科·卡西尼(Giovanni Dominico Cassini，1625-1712)出生于意大利，任教于博洛尼亚大学(Bologna)，但在皮卡德的不懈努力下，于1668年辞去职务，成为新成立的巴黎天文台台长。改名为让·多米尼克(Jean Dominique)后，他对天文学做出了重大贡献：确定了火星和木星的自转周期，首次研究了黄道光(一种微弱的光，在日出前在东方天空伸展，在日落后在西方天空伸展)，发现土星的四颗卫星和土星环中的暗缝(称为卡西尼分部)，以及1672年对火星视差的测量，据此他能够使用开普勒行星运动定律计算出地球到太阳的距离为8700万英里，第一个测定值接近实际值约9350万英里。 令人惊讶的是，他还是最后一位反对哥白尼日心说的专业天文学家之一，尽管有越来越多的相反证据，他仍然坚信地球是一个长球体。[11]

在晚年，卡西尼越来越多地致力于大地测量学和制图学，充分利用他的天文专业知识。 1679 年，他构思了一幅新的世界地图，即“ planisph`ere terrestre”，使用的投影可以正确显示北极的所有方向和距离；这被称为“等距方位投影(azimuthal  equidistance projection)”(见第10章)。卡西尼号巨大的地图，直径24英尺，绘制在巴黎天文台的三楼；它成为未来制图师的典范，并于1696年被复制并出版。

但卡西尼号并没有因此而满足。 现年70 岁的他在儿子雅克(Jacques，1677-1756 年)的协助下，以新的活力重新开始了对法国的考察。他们的目标是：将勘测范围向南延伸至比利牛斯山脉，并最终以三角形网络覆盖整个欧洲。作为副产品，他们希望找出地球是扁圆形(prolate)还是扁圆形(oblate)。

老卡西尼号于1712年去世，享年87岁。他的儿子现在意识到这个问题只能通过比较相隔很远的纬度的度数长度来解决，他建议派探险队到赤道和北极地区一劳永逸地解决这个问题。危在旦夕的不仅是对地球形状的理论兴趣；法国本身的威望处于平衡之中。牛顿曾预言地球在两极是扁平的，他的论点基于地球自身的引力与地球自转产生的离心力之间的相互作用。然而在法国，牛顿的万有引力思想——尤其是他的“远距离作用”的概念被拒绝，支持笛卡尔的涡流理论(theory of vortices)，该理论认为引力是由弥漫在所有空间的流体中旋转的巨大涡流引起的。“地球的形状已经成为一个大事件，成为当今争论最激烈的科学问题，法国和英国的民族自豪感岌岌可危。”[12]

证据虽然是间接的，但倾向于支持牛顿。 其一，即使是通过小型望远镜观察到的木星，也显示出两极相当平坦；在地球上，从摆动周期获得的重力加速度测量结果显示，赤道的值比两极的值略小，这表明赤道离地球中心的距离比两极离地球中心的距离远。

根据雅克·卡西尼的建议，并在新君主路易十五的支持下，法国皇家科学院(Acad´emie Royale de Sciences)——在法国相当于英国的皇家学会——于 1734 年批准了两次探险，其中一次派往瑞典-芬兰接壤的拉普兰，另一次派往与靠近赤道秘鲁。 他们的任务是：对各自区域进行全面三角测量，并确定每个位置的度数长度。

第一次远征由 Pierre Louis Moreau de Maupertuis(1698-1759)率领，他在法国军队开始了他的职业生涯，后来成为数学家和物理学家(他是第一个制定最小作用原理的人，后来用它来“证明”上帝的存在)。 作为牛顿在大陆的唯一支持者和崇拜者，他非常渴望加入一项他希望能证明他的主人是正确的努力。随便而去的是另一个法国数学家，Alexis Claude Clairaut(1713–1765), 作为神童，他十岁时学习了微积分，十八岁时出版了他的第一本书(微分方程xy’ – y = f(y’)，其中，f是导数为y’的已经函数, 是以他的名字命名的)。秘鲁探险队由地理学家查尔斯·玛丽·德拉康达明(Charles Marie de La Condamine，1701-1774 年)率领，其中还包括一位数学家皮埃尔·布热(Pierre Bouger，1698-1758年)。如此多的一流数学家参与偏远国家的实地考察，符合法国培养杰出科学家的悠久传统，这些科学家也在军队和文职部门为国家服务。我们将在第15章中遇到更多的人。

两次出征都遇到了重重困难。拉普兰队冒着令人眼花缭乱的暴风雪，不得不强行穿越在春天到来时变成泥泞的冰冻沼泽地；在夏天，他们最大的敌人是叮咬的蚊子。秘鲁队的情况更糟：他们不仅在安第斯山脉高原上与高原反应作斗争，而且疾病和一系列事故导致数名成员死亡。最糟糕的是，远征队领导人之间爆发了激烈的异议，他们分别返回家园。尽管如此，这两次探险还是完成了他们的任务：他们发现拉普兰的度数长度为69.04英里，秘鲁的度数为68.32英里(图 24)。结合皮卡德在巴黎的68.65英里的数值，他们的结果毫无疑问地证明了地球是一个扁球体。牛顿再次被证明是正确的。

-----------图24 测量经度。该地图显示了莫佩尔图伊斯(Maupertuis)的拉普兰探险队建立的三角测量网络的一部分。来自 1798 年的版画(作者的收藏)。-------------------

现在卡西尼号又回到了现场。当这两次探险在国外开展工作时，雅克·卡西尼和他的儿子凯撒·弗朗索瓦(C´esar François，1714-1784年)使用由18个基线和400个三角形组成的网络完成了法国的三角测量。现在剩下的工作就是将网格转换为实际地图，这项任务由王朝创始人的曾孙让·多米尼克·卡西尼四世(Jean Dominique Cassini IV，1748-1845年)完成。他的巨幅地图为 12 × 12 码，以 1:86,400的比例出版了182张，不仅显示了地形特征，还显示了城堡、风车、葡萄园以及——当时正值法国大革命——断头台的位置。四号卡西尼号的工作获得了很多赞誉——然后被捕并被革命法庭审判，勉强保住了性命。他的名誉最终被拿破仑波拿巴恢复，于1845年去世，享年九十七岁。

法国在大地测量方面的领先地位现在被欧洲其他国家效仿，到19世纪中叶，欧洲大陆的大部分地区都被彻底地三角化并绘制了地图。1800年至1913年，一项被称为大三角测量的巨大三角测量项目随后转移到海外，转移到大英帝国皇冠上的明珠印度。由东印度公司赞助，这家庞大的商业企业实际上统治了从其位于伦敦的办事处开始，从孟加拉湾西南海岸的马德拉斯附近开始，最终到达最北端的喜马拉雅山的国土。

威廉·兰姆顿船长(William Lambton)(1753-1823年)从1802年到去世一直领导勘测，他决心以前所未有的准确性实现他的目标。他的巨大经纬仪(theodolite)重达半吨，是根据他的具体指示在伦敦建造并运往印度的，途中被法国护卫舰拦截。有一次，这个巨大的仪器被吊到坦焦尔大神庙(Great Temple of Tanjore)(坦贾武尔)的顶部，以便让测量员(surveyors)清楚地看到地形(terrain)。在上升的过程中，一根绳子(rope)断了(snapped)，仪器掉在地上摔坏了。Lambton毫不畏惧(Undaunted)，躲在帐篷里，在接下来的六周内亲自修理了仪器。

1806 年，Lambton着手实现一个比勘测印度更伟大的目标：确定地球的形状。 为此，他沿着北纬78度经线从次大陆南端的科摩林角(Cape Comorin)附近一直延伸到北部的克什米尔地区，全长约1,800英里。 他的手下遇到了无数危险：印度中部的酷热、老虎在其中漫游的茂密植被、随时存在的疟疾(malaria)威胁，以及愤怒的当地人，他们相信测量员正在监视(spying on)他们的妻子。

Lambton 去世后，这项调查在他的助手George(后来的乔治爵士)Everest(1790-1866 年)的领导下继续进行，后者后来成为印度测量长官。Everest保持甚至超过了他的前任的高标准。为了弥补印度中部广袤平原上自然地标的缺失，他建造了一系列从远处就可以看到的塔楼，其中许多塔楼至今仍屹立不倒。为了避免这个国家内陆的高温和雾霾(haze)，他命令他的测量员在晚上工作，依靠从他的塔楼顶部点燃的篝火作为信号。白天，他使用日光仪——一种特别设计的镜子，从50英里外就可以看到反射的阳光。Everest对细节的一丝不苟得到了回报：当勘测到达喜马拉雅山脚下时，他的实际位置与三角测量计算的位置相差7英寸，距离为500英里！

-------------------------图25 十九世纪的测量仪器-------------------------

在Everest勘察的过程中，他发现了一个至今仍在争论不休的发现：他发现巨大的喜拉雅山脉使铅垂线(plumb line)的方向发生了偏转(deflected)。这些重力异常是现在所谓的“mascons”(质量浓度，该术语首先应用于月球)的第一个迹象，其确切的性质和分布今天正在通过卫星绘制。

1843年Everest退役后，勘测工作在他的助手安德鲁·沃(Andrew Waugh)船长的指导下继续进行。 现在，三角函数测量遥远物体的能力达到了它的最高点——字面意义上的。 传说在1852年的一天，该调查的首席计算机、数学家Radhanath Sikdar冲进Waugh的办公室，大声说：“先生，我发现了世界上最高的山峰。” 官方的公告被推迟到1856年，以检查和重新检查第十五峰的高度，临时命名为珠穆朗玛峰(Mount Everest)(它的藏文名称 Chomolungma，“世界的女神之母”)。在大约100英里的距离处获取的几次读数的平均值，结果表明这座山的高度正好是29,000英尺；但担心这样的圆形数字看起来像是虚构的，测量员武断地加上了两英尺，直到1954年，世界最高峰的官方高度仍保持在海拔29,002英尺。它现在的高度值为29,028英尺。[13]

当法国人忙于对欧洲进行三角测量，而英国人则在调查他们的帝国时，德国的弗里德里希·威廉·贝塞尔(Friedrich Wilhelm Bessel，1784-1846年)则着手对天空进行三角测量。 他的职业生涯始于一名会计师，自学了数学和天文学，并在20岁时重新计算了哈雷彗星(Halley’s comet)的轨道，同时考虑了行量木星(Jupiter)和土星(Saturn)对其施加的引力扰动。Bessel的成就使他引起了当时领先的德国天文学家海因里希·奥尔伯斯(Heinrich Olbers)的注意，后者为他确保了在李林塔尔天文台的职位。1809年，他被任命为位于哥尼斯堡(今俄罗斯加里宁格勒)的普鲁士皇家天文台台长，他作为一名技术娴熟的观测天文学家和一流的理论家享有盛誉，他一直担任这一职位直至去世。[14]

到1800年，当时已知的太阳系的大小已经相当确定(尽管行量海王星(Neptune)和冥王星(Pluto)尚未被发现)，但宇宙之外的维度是另一回事：没有人对太阳系恒星具体有多远有任何概念。视差法在确定太阳系物体的距离方面如此成功，但在应用于恒星时却失败了：即使使用我们可用的最大基线——地球绕太阳公转的直径,也没有恒星显示出任何可测量的位置变化。事实上，希腊人认为不存在视差是他们所描绘的宇宙图景的最有力证据，在这个宇宙中，静止不动的地球永久固定在中心。哥白尼对事实的解释不同：对他来说，没有任何可辨别的视差表明恒星离我们如此之远，以至于由于地球绕太阳运动而导致的任何明显的位置变化都太小，我们的眼睛无法检测到。

当望远镜于1609年发明时，从理论上讲可以寻找一些附近恒星的视差，但所有这些尝试都失败了。一个原因是天文学家只关注天空中最亮的恒星，并假设它们的亮度表明它们也是最近的。如果所有的恒星都具有相同的固有亮度——相同的光输出——就像街道上的路灯一样，那么这就是正确的。但是到1800年，天文学家知道恒星的固有亮度差异很大，因此它们的表观亮度(apparent brightness)不能用作估计它们的相对距离的有效标准。相反，搜索转向了具有较大固有运动(proper motion)的恒星——恒星相对于遥远天空的实际运动(与表观运动相反，表观运动仅仅是由于观察者自身的运动)。人们正确地假设，一个大的固有运动将表明这颗恒星相对较近。

很快就找到了一个候选者——天鹅座中心(constellation Cygnus)的天鹅座61号行星。 这颗五等星肉眼几乎看不见，但众所周知它有相当大的固有运动——每年5.2角秒，或每 350年大约一个月球直径。贝塞尔现在将所有的努力都指向了这颗恒星。经过 18 个月的紧张观察，他于1838年宣布天鹅座61的视差为 0.314 弧秒(相比之下，月球的视直径约为半弧度，即 1,800 弧秒)。这个微小的数字足以让贝塞尔使用最简单的三角函数计算得出恒星的距离。由于这一事件标志着天文学史上的一个里程碑，我们在此提供详细信息。

在图26中，令S表示太阳，E1  和 E2  表示地球没太阳公转轨道上相的两点，T表示问题中的恒星，根据天文学惯例，年度视差定义为由于地球绕太阳公转而产生的恒星位置角位移的一半,即在直角三角形E1ST中，角α  = ∠E1TS 。帮d表示到恒星的距离,用r表示地球轨道首径，我们有sin(α) = r/d，或者

d = r / sin(α)

代入r = 150,000,000 km =  km 以及α = 0.314’’ = (0.314/3600)°，我们得到

d =  km。所以我们必须用这个数字除以光速， km/s。时间是乘以一年中的称数，3,600×24×365。从而算出，d = 10.1 光年。

因此，我们太阳系以外的宇宙维度为人所知。61 Cygni的视差已经改进为0.294’’， 距离为 11.1 光年。很快，其他恒星的视差也被成功测量，其中包括半人马座阿尔法星(Alpha Centauri)的视差，它距离我们4.3光年，是太阳以外距离我们最近的天体。[ 15] 该方法已应用于距离约一百光年的恒星，但当应用于更远距离时，它的准确性迅速降低。幸运的是，在努力建立可靠的恒星距离尺度的过程中，已经开发出基于恒星物理特性的其他方法。

-------------------------图26 十九世纪的测量仪器-------------------------

1844 年，Bessel有了第二个划时代的发现：他将望远镜对准天空中最亮的恒星天狼星(Sirius)，发现它的自行显示出微小的波浪状图案；他正确地将此归因于围绕天狼星旋转的无形伙伴的引力影响。这个伴星天狼星B于1862年由美国望远镜制造商阿尔文·格雷厄姆·克拉克(Alvan Graham Clark，1832-1897 年)发现。

在Bessel一生的大部分时间里，引力摄动一直占据着他的脑海。这个主题提出了天体力学中最困难的问题之一，为了解决这个问题，他引入了一类被称为“Bessel函数(Bessel functions)”的函数。这些是微分方向，其中， n ≥ 0 是个常量(并非一定是整数)。解的特征在很大程序上取决于 它们可以根据函数x写成封闭的形式，sin x和cos x; 否则它们只能表示为无穷级数，因此被认为是“非初等”或“高等”函数。Bessel方程出现在许多应用中；例如，圆形膜(membrane)(如鼓皮)的振动是受n = 0时的贝塞尔方程支配的。[16]

在他生命的尽头，Bessel再次转向引力摄动问题。当时悬而未决的天文学谜团之一是天王星运动的异常：所有试图将这些异常解释为由已知行星(尤其是木星和土星)引起的尝试都失败了。Bessel正确地将它们归因于一颗未知的超铀行星的存在，但他在这颗行星海王星被发现前几个月就去世了。

Bessel是最后一位在理论和实验(在本例中为观察技术)方面同样游刃有余的伟大科学家之一。数学家们会因为Bessel函数而记住他，但他的最高成就是为我们提供了星际空间究竟有多大的第一个具体证据。有了他，天文学家的注意力开始从太阳系转移到更远的宇宙。

注释和资料来源：

1. 见Thomas. L. Heath先生，<> (1913初版; New York: Dover, 1981年再版)，以及<< Greek Astronomy>>(1932初版; New York: Dover, 1991年再版)。

2. 这可以从这个事实推断，即，在0°< x <90°时，函数(sin x)/x是递减的；而函数(tan x)/x在这个范围内是递增的；即，(sin α)/ α < (sin β)/ β 且 (tan α)/α > (tan β)/ β。

3. 1995 年，我和一群天文学家一起去印度探险，观看10月24日的日全食。从我们靠近月球阴影中心线的视线看，全食只持续了41秒。

4. 引用自Bryan Brewer，<>(日食)(Seattle: Earth View, 1978)，第31页。

5. 参见Albert van Helden，<>(测量宇宙：从阿里斯塔克斯到哈雷的宇宙维度)(芝加哥：芝加哥大学出版社，1985年)，第11页。另见Toomer在DSB(Dictionary of Scientific Biography)中关于Hipparchus的文章。

6. 许多学术辩论都致力于体育场的长度。一些消息来源称它等于十分之一英里，或 528 英尺，这将导致25,000英里的周长。不过，回想起来，这个体育场的长度似乎已经被“固定”，以便使周长接近现代价值。引用B. L. van der Waerden在<>(科学觉醒)(New York: John Wiley,1963)第230行的话说就是：“由于我们不知道体育场的确切长度，我们只能说 [地球周长] 的数量级是对的。” 另见David Eugene Smith，<>(数学史)(1925初版; New York: Dover, 1958年再版)，第2卷，第641页。

7. 后面的叙述基于下面的资料：Lloyd A. Brown<>(地图的故事)(1949初版; New York: Dover, 1979年再版)；John Noble Wilford, <>(地图的标识)( New York: Alfred A. Knopf, 1981年版)；以及Simon Berthon和Andrew Robinson，<>(世界的形状)( Chicago: Rand McNally, 1991出版)。

8. 他的真名是杰玛·雷尼尔(Gemma Regnier)，但在他的出生地弗里斯兰(Friesland)之后，他被称为杰玛·弗里西乌斯(Gemma Frisius)。1541年，他成为鲁汶大学的医学教授。他的算术书(安特卫普，1540 年)非常受欢迎，发行了不下60版。他还写了地理和天文学，并提出了根据两地当地时间的差异来确定经度的方法。他的儿子Cornelius Gemma Frisius(1535-1577年)继承了他父亲的工作，并在同一所大学担任医学教授。

9. 他是莱顿大学的数学教授，在那里他接替了他的父亲。他研究天文学、物理学和球面三角学，最著名的是他的光学折射定律。

10. 直到1913年，法国才承认通过格林威治的子午线为本初(零)子午线，以换取英国“承认”公制。

11. 1997年10月美国宇航局发射升空，前往土星进行为期七年的航行的卡西尼号宇宙飞船就是以他的名字命名的。

12. 引自Berthon和Robinson的<>(世界的形状)第101页。

13. 令人惊讶的是，埃德蒙·希拉里爵士在他的自传<> (没有冒险，没有成功)( New York: Coward, McCann & Geoghegan, 1975年)中，他与夏尔巴人Tenzing Norgay于1953 年率先登上珠穆朗玛峰，仍然给出这座山的高度为 29,002 英尺——在正式更改后二十多年。1994年，一个中国测量队在全球卫星定位系统的帮助下，将这个数字定位在 29,023 英尺处。

14. 参见DSB(Dictionary of Scientific Biography)中Walter Fricke关于Bessel的文章。

15. 实际上，半人马座阿尔法星是一个三合星系统，其最暗的伴星比邻星(发现于1915年)目前距离我们4.2光年。61天鹅座现在在距离太阳的距离排序中排在第十九位。参见Joshua Roth 和 Roger W. Sinnott 所写的文章“Our Nearest Celestial Neighbors (我们最近的天体邻居)”，Sky & Telescope 期刊，1996年10月，第32到第34页。

16. 对于n = 0和1，Bessel函数——分别用  和 , 并且这两个函数都有一个振荡图。然而，它们的振幅随着x的增加而减小，并且它们的零点在x轴上的分布不均匀，这就是为什么鼓的声音不同于小提琴的声音(见第15章)。有关详细信息，请参阅任何有关常微分方程的书籍。

5.2. Abraham De Moivre在天体和地球测量中的数学贡献

Abraham De Moivre 于1667年5月26日出生于法国香槟省维特里的一个新教家庭。 他很早就表现出对数学的兴趣，并在他就读的各种宗教学校秘密地研究它。1685 年，路易十四废除了南特敕令——一项于1598年颁布的授予法国新教徒宗教自由的法令——随后是一段镇压时期。一种说法是，德莫弗(De Moivre)在前往伦敦之前被监禁了两年，他将在那里度过余生。他自学数学，并且精通数学。非常幸运的是，他碰巧在德文郡伯爵的家里，他在那里当家庭教师，就在艾萨克·牛顿(Isaac Newton)带着一本他关于引力理论的伟大著作<>走出去的那一刻。De Moivre 拿起这本书，自己研究，发现它比他预期的要难得多(甚至对于现代读者来说，读起来都非常困难)。但通过刻苦学习——他过去常常从这本巨著中撕下几页，以便在辅导课期间研究它们——他不仅掌握了这项工作，而且成为了这方面的专家，以至于牛顿在后来的几年里提到了对De Moivre 向自己提出的问题，他说：“去找De Moivre先生；他比我更了解这些事情。”

1692 年，他遇到了埃德蒙·哈雷(Edmond Halley)(因彗星成名)，Halley对自己的数学能力印象深刻，以至于他向皇家学会德莫伊弗(De Moivre)的第一篇论文传达了牛顿的“流变法”(即微积分)。通过Halley，De Moivre成为牛顿朋友圈的一员，其中还包括约翰·沃利斯(John Wallis)和罗杰·科特斯(Roger Cotes)。1697年，他被选入皇家学会，并于1712年被任命为该学会委员会的成员，以解决牛顿和莱布尼茨之间关于微积分发明的激烈争论。 他还被选入巴黎和柏林的学院。

尽管取得了这些成功，德莫伊弗还是无法确保自己获得大学职位——他的法国血统是一个原因——甚至连莱布尼茨代表他的尝试都没有成功。他作为数学导师过着微薄的生活，在他的余生中，他会感叹不得不浪费时间在学生的家之间穿梭。他的空闲时间是在圣彼得堡的咖啡馆和小酒馆度过的。 在伦敦的马丁巷，他回答了富有的顾客向他提出的各种数学问题，尤其是关于他们在赌博中获胜的机会。

当他变老时，他变得昏昏欲睡，需要更长的睡眠时间。根据一种说法，他宣称从某一天开始，他以后的每一天都需要多睡20分钟。在第七十三天——1754年11月27日——当额外的睡眠时间累积到24小时时，他去世了；正式原因被记录为“嗜睡(somnolence)” (sleepiness)。他87 岁时，加入了众多年过80岁的杰出英国数学家行列：William Oughtred(卒于1660 年，享年 86 岁)、John Wallis(卒于1703 年，享年87岁)、Isaac Newton(卒于1727年，享年 87 岁) , Edmond Halley (卒于1742年，享年86岁), 以及在我们这个时代的 Alfred North Whitehead (卒于1947年，享年 86 岁) 和Bertrand Russell，1970 年去世，享年98岁。诗人Alexander Pope在诗歌<>(人论)中对他致敬：

Who made the spider parallels design,  (是谁设计了蜘蛛平行图案，)

Sure as Demoivre, without rule or line?  (如Demoivre，无需规则和线条？)

De Moivre的数学工作主要涵盖两个领域：概率论以及代数和三角学(被视为一个统一的领域)。很可能他扩展了前任的工作，特别是克里斯蒂安·惠更斯(Christiaan Huygens)和伯努利家族(Bernoulli family)的几位成员。Huygens首先提出的一个问题的概括被称为 De Moivre 问题(De Moivre’s problem)：给定n个骰子，每个骰子有f个面，求掷出任意给定点数的概率。[1] 他在这个领域的许多研究出现在他的著作<< The Doctrine of Chances: or, a Method of Calculating the Probability of Events in Play>>(概率学术：或，一种计算游戏中事件发生可能性的方法)( London，1718 年，1738 年和 1756 年增订版)；它包含许多关于掷骰子、从袋子里抽出不同颜色的球以及与终身年金有关的问题。这里还陈述了(虽然他不是第一个发现它的人)寻找复合事件概率的定律。第二部著作<< A Treatise of Annuities upon Lives>>(生存年金论)(伦敦，1725 年和 1743 年)涉及死亡率统计分析(Halley早在几年前就开始了)、几位继承人之间的年金分配，以及金融界感兴趣的其他问题机构和保险公司。

在概率论中，人们经常遇到表达式 n！(读作“n阶乘”)，定义为1.2.3.....n。n!的值随着n的增加而快速增长；例如，10！=3,628,800而20！=2,432,902,008,176,640,000。要求 n! 必须首先找到 (n–1)!，这又需要找到(n–2)!依此类推，直接计算n!对于大数值的n来说非常耗时。因此，希望有一个近似公式通过一次计算来估计n! 的值。在一篇写于 1733 年并私下呈现给一些朋友的论文中，De Moivre 开发了公式

其中，c是一个常，e是自然对数的基底。[2] 然而，他无法确定这个常数的数值。这项任务落在了苏格兰人詹姆斯·斯特林(James Stirling，1692-1770年)的肩上，他发现 。因此，正如今天所知，斯特林的公式在很大程度上归功于德莫弗尔；它通常写成下面的形式

 。

例如，对于n = 20，公式求出的值为 2.422,786,847× , 与正确的值相比，约等于的值为 2.422,902,008× 。

De Moivre 的第三部主要著为<>(杂项分析)(London，1730 年)除概率外还涉及代数和解析三角学。在这一时期的主要问题是，如何将形如  这样的多项式因式分解成二次的因子(quadratic factors)。这个问题与Cotes 将比率表达式分解为部分分数(当时称为“循环级数(recurring series)”)的工作有关。De Moivre完成了Cotes因早逝而未完成的这项工作(见第182页)。在他的众多结果中，我们发现了以下公式，有时被称为“Cotes圆的性质”：

为了求得这个因式分解，我们仅需求得(使用De Moivre的定理)方程  的不同的根，即，的2n个复值(complex values)，然后将相应的线性因子乘以共轭对(conjugate pairs)。事实上，三角表达式出现在诸如  这样的纯粹的代数表达式的因式分解中，会使得所有第一次遭遇这样的公式的学生感到惊呀；在De Moivre的年代，它甚至让专业数学家都感到震惊。

    De Moivre的著名定理

由他在1722年提出，但从未在他的著作中明确说明；然而，他知道，从以下公式可以很清楚地说明

这个公式是他在1707年发现的(De Moivre推断这个公司对正整数的n值成立；Euler在1749年证明对于所有实数n这个公司都成立)[3]。 他经常在<>中引用它，并在他发表在皇家学会(Royal Society)官方期刊“Philosophical Transactions”上的许多论文中使用它。例如，在他1739年发表的论文中，他说明了如何求得形如  或  这种二项式(binominal)的根(他称后者为“不可能的二项式”)。作为一个专门的例子，他演示了如何求得  的三次方根(用现代的记法为)。这里的讨论只是叙述式的而非系统化的，但这正是我们今天在任何三角学教科书中都能找到的方法： 按照极坐标公式r(cosθ + isinθ)的写法， 

和

 。

计算出这个表达式为  [(cos(θ+360°k)/3+ isin(θ+360°k)/3]，k = 0, 1, 2。我们有

 ，θ/3 = 10.89°。因此，根是  cis (10.89°+ 120°k),其中，其中，“cis”表示“cos+isin”。使用表或者计算器可以求得正弦和余弦值,我们就得到三个所求的根：

, ，以及 。De Moivre补充道：

有几位作者，其中最著名的是 Wallis，他们认为那些与圆相关的三次方程可以通过求得虚数(imaginary quantity)和 的立方根来求解 ，而无需考虑正弦查求，但这仅仅是虚构的，是在回避问题。因为在尝试时，结果总是再次回到与第一次提出的相同问题。如果没有正弦表的帮助，这件事就不能直接完成，尤其是当根是非比率数(irrational)时，正如许多其他人所观察到的那样。

De Moivre肯定想知道为什么这三个根会以“漂亮(nice)”的非比率复数形式出现，即使角度不是像15°,30°,45°这样的任何“特殊”角度；他说，在没有正弦表的情况下求复数的立方根是“虚幻的(fiction)”(即不可能的)；为了避免任何误解，他在结尾处再次重复了这句话：“如果没有正弦表的帮助，这件事就不能直接完成，尤其是当根是非比率数时。” 在一般情况下他当然是对的：求一个复数z = x + iy的三个立方根，我们必须将其表示成极坐标的形式，z = cis θ , 其中， 且 ；下一步我们计算出和θ/3 ，则——通过查正弦表——我们求得cos( θ/3)和sin( θ/3)，以及最后求得 cis (θ/3 + 120°k)，k = 0，1，和2。然而，颇具讽刺意味的是，恰恰是De Moivre用来说明过程的例子却偏偏可以在不求助于正弦表的情况下求解！且看下面分析如何做到。我们的目的是求得式子  r cis θ 的三个立方根，其中以及。从最后一个方程(或通过直接计算x/r)，我们可以求得 。现在我们使用这个恒等式，求得cos(θ/3)的值；令 x = cos(θ/3)，我们有

 -------------(1)

或

 -------------(2)

将   代入公式，以上公式简化为方程

-------------(3)

这个新方程没有自由基(radical-free)，但它的前导系数看起来大得令人绝望。然而，碰巧 147可以被21整除，而333,396可以被213整除。写成 z = 21y，等式变成\

 ，-------------(4)

这是一个非常简单的方程，其3个根分别为1/2，-1/3和-1/6——所有的数都是比率数！再替换回去，我们得到y = z/21 = 1/42，-1/63和-1/126 ,最后求得 x = cos (θ/3) =,,以及 。对于这些解中的每一个解，我们现在从恒等式

求得sin (θ/3)；我们求到sin (θ/3) =，,和(最后一个值是负值，这是因为它对应的是复平上的第III象限)。此外，我们有

 。因此，这三个所求的根分别为

 ，

  ，

和

 ；

如图27所示。

-----------------图27  的3个立方根---------------------------

当然，处理这个问题的“自然”的方式或许应当是直接求解方程(1)，方法是使用以意大利人 Girolamo Cardano(也称为Jerome Cardan，1501-1576)命名的公式求解。这个公式实际上是由另外两个意大利人独立开发的 ,即由Scipione del Ferro(约1465-1526年)和Nicolo Tartaglia(约1506-1557年)开发。Cardano的公式类似于我们熟悉的求解二次方程的二次公式，但要复杂得多；它基于这样一个事实，即任何正规形式的三次方程  都可以通过将等 式y = x - a/3代入等式，将其简化为简约形式 (没有二次项的项),其中， 以及 。因为方程(1) 已经没有二次项，我们仅需用前导系统去除它，应用, 得到p = -3/4， 。现在，Cardano的公式要求你计算这个量

 和  。将p和q代入这些表达式并经过大量简化后，我们得到

 ，。因此，现在我们必须求得复数 的立方根，要完成这一步，我们必须将其以极坐标的形式表示为R cis Φ 。因此，我们有，

  

且

 

——与我们最初的角度完全相同！ 这就是 De Moivre 在他神秘的陈述中的意思，“因为在尝试它时，结果总是再次回到与最初提出的同一个问题。”

De Moivre这种水平的数学家会不会忽略了一个事实，即他自己的例子可以不使用正弦表来解决？显然他做到了。 甚至爱因斯坦也曾经忽略了他的一个方程式中的分母可能为零的可能性。那是在 1917 年，当时他将广义相对论应用于宇宙学问题。一位年轻的俄罗斯天文学家亚历山大·弗里德曼 (Aleksandr Friedmann)注意到了这种看似良性的疏忽，并得出结论认为，爱因斯坦忽略的特殊情况至少暗示着宇宙可能正在膨胀！[6]

注释和资料来源：

1. Florian Cajori，<< A History of Mathematics>>(数学史)(1893年初版；New York:Macmillan, 1919第二版)，第230页。

2. 这篇论文还给出了正态分布(normal distribution)公式的第一个表达式。见David Eugene Smith，<>(一本数学原始文献书) (1929年初版；New York:Dover, 1959重印本)第566-568页。

3. 从这个关系和其关联关系，

通过相加，我们得到

从此，立即就可以导出后面的Florian Cajori定理。至于Euler对这个公式对任意实数n都有效的证明，参见Smith数学史的第452-454页。

4. 参见同上，Smith数学史的第447-450页。似乎这两个根  和  存在明显的错误。可能是排版错误造成的。

5. 三次方程的历史很长，充满了争议和阴谋。见David Eugene Smith的<>(数学史)( 1925初版；New York: Dover, 1958重印)卷2第 456-466页；Victor J. Katz的<>(数学史：概观)( New York: HarperCollins，1993年版)第328-337页；以及David M. Burton<< History of Mathematics: An Introduction>>(数学史：概观) (Dubuque, Iowa: Wm. C. Brown，1995年版)第288-299页。

6. Ronald W. Clark，<>(爱因斯坦：生命与时光)( 1971初版; New York: Avon Books, 1972年重印)。

内容来源：

<> 作者：Eli Maor