Python自动进行统计描述（分别计算各组的样本量、样本均数和样本标准差，绘制条形图）、正态性检验（绘制频数图）、方差齐性检验、单因素方差分析、两两相比

简介

单因素方差分析（one-way ANOVA）是一种参数检验，

用于统计推断不同组（组数≥2）的总体平均数是否相同。

使用条件

使用这一统计推断方法需要满足以下条件：

①连续资料：

被分析的资料必须为连续资料，

例如身高、体重、血红蛋白浓度、血清肌酐浓度等等。

（通俗一点理解，可以精确到小数点后面很多很多位。

例如身高，可以表示为2m，也可以表示为2.1m，或2.11m，或2.111m等等）

②独立：

即采用完全随机设计来获得这一连续资料，

例如将患者随机分为3组，并测量每一个人的血红蛋白浓度。

③正态分布：本文使用Shapiro Wilk法来进行正态性检验

④方差齐性检验：本文使用Bartlett法来进行方差齐性检验

当同时满足以上4种条件时，才可以进行单因素方差分析。

首先，自定义函数one_way_anova(y,x,df,histogram=False)，将统计描述（分别计算每组的样本量、样本均数和样本标准差，绘制条形图）、正态性检验（频数图、Shapiro Wilk法）、方差齐性检验（Bartlett法）、单因素方差分析、两两比较（tukey法）进行打包：

from scipy.stats import shapiro,bartlett
import statsmodels.api as sm 
import statsmodels.formula.api as smf
from statsmodels.stats.multicomp import pairwise_tukeyhsd
from plotnine import *

def one_way_anova(y, x, df, histogram=False): # one_way_anova(y是连续变量的列名, x是分类变量的列名, df是数据框名)，例如one_way_anova('Hb','group', df)
    print("==============================================================================")    
    """统计描述"""
    print (f'根据{x}进行分组，对{y}进行统计描述:')
    print(df.groupby(x)[y].agg(["count","mean", "std"]))  #根据group分组，分别计算各组的样本量、样本均数和样本标准差   
    '''绘制条形图：mean~sd'''
    print(ggplot(df, aes(y=y,x=x))
          +geom_bar(stat='summary',width=0.5)
          +stat_summary(fun_data='mean_sdl', # 使用均值和标准差来计算误差线的高度范围
                        fun_args={'mult':1}, # 将标准差乘以1来计算误差线的高度
                        geom='errorbar', # 绘制误差线
                        width=0.3)
          +theme_bw())
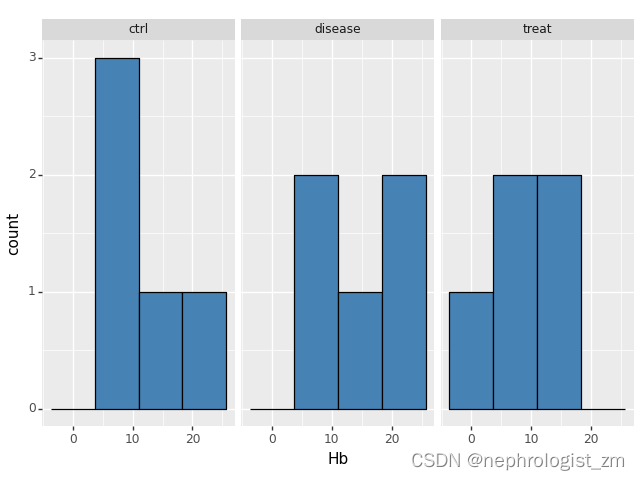
    '''绘制直方图'''
    if histogram:
        print(ggplot(df)
              + aes(x=y)
              + geom_histogram( fill='steelblue', color='black')
              + facet_wrap(f'~{x}'))  # 分面设置，按制造商进行分面
    '''正态检验：Shapiro Wilk'''
    print (f'根据{x}进行分组，对{y}进行正态检验（Shapiro Wilk）:')        
    data_for_analysis = []
    for category,value in df.groupby(x)[y]:
        w,p = shapiro(value)
        print(f'{category}: w={w:.6f}     p={p:.6f}')
        data_for_analysis.append(value)             
        if p<0.05:
            print(f'因为正态检验（Shapiro Wilk）的p为{p:.6f}＜0.05，所以进行非参数检验')
            return   
        
    '''方差齐性检验：Bartlett'''
    stat, p =bartlett(*data_for_analysis)
    print(f'\n\n方差齐性检验（Bartlett）：\nstat={stat:.6f}   p={p:.6f}')    
    if p<0.05:
        print(f'因为方差齐性检验（Bartlett）的p为{p:.6f}＜0.05，所以进行非参数检验')
        return     
    
    '''one-way ANOVA'''
    print ('\n\n因为既正态分布又方差齐，所以进行one-way ANOVA:')
    model = smf.ols(f"{y}~{x}",  # 因变量y是连续变量~自变量x是分类变量
                    data = df).fit()
    result = sm.stats.anova_lm(model) # df 是自由度（degrees of freedom
    p=result.loc[x,"PR(>F)"] # sum_sq是平方和（sum of squares
    print(result)                     # mean_sq是均方误差（mean-squared deviations

    '''两两比较'''
    if p>0.05:        
        print (f'\n\n因为one-way ANOVA的p为{p:.6f}>0.05，所以无需两两比较:')
    else:  
        print (f'\n\n因为one-way ANOVA的p为{p:.6f}＜0.05，所以使用Tukey法进行两两比较:')
        compare = pairwise_tukeyhsd(endog = df[y], # 连续变量
                                    groups = df[x], # 分类变量
                                    alpha=0.05)
        print(compare)
    print("------------------------------------------------------------------------------")

 如何在其他.py文件中调用自定义函数one_way_anova(y, x,df,histogram=True)可参考http://t.csdn.cn/ovlRZ

随后准备数据：

import pandas as pd

df = pd.DataFrame()
df['group'] = ['ctrl','ctrl','ctrl','ctrl','ctrl','disease','disease','disease','disease','disease','treat','treat','treat','treat','treat']
df['Hb'] = [15, 22, 7, 8, 5, 15, 23, 8, 19, 10, 15, 1, 8, 7, 15]
df

可见df有2列（即2个变量，其中group是分类变量，Hb是连续变量，代表血红蛋白浓度）

以后只要调用自定义函数one_way_anova(y,x, df,histogram=True)即可自动进行统计描述（计算每组的样本量、样本均数和样本标准差，绘制条形图）、正态性检验（绘制频数图、Shapiro Wilk法）、方差齐性检验（Bartlett法）、单因素方差分析、两两比较（tukey法），例如：

one_way_anova(y='Hb',x='group', df=df,histogram=True)

输出为：

==============================================================================
根据group进行分组，对Hb进行统计描述:
         count  mean       std
group                         
ctrl         5  11.4  7.021396
disease      5  15.0  6.204837
treat        5   9.2  5.932959


根据group进行分组，对Hb进行正态检验（Shapiro Wilk）:
ctrl: w=0.887557     p=0.344966
disease: w=0.957299     p=0.789060
treat: w=0.896618     p=0.391479


方差齐性检验（Bartlett）：
stat=0.111916   p=0.945579


因为既正态分布又方差齐，所以进行one-way ANOVA:
            df      sum_sq    mean_sq         F   PR(>F)
group      2.0   85.733333  42.866667  1.045528  0.38144
Residual  12.0  492.000000  41.000000       NaN      NaN


因为one-way ANOVA的p为0.381440>0.05，所以无需两两比较:
------------------------------------------------------------------------------

 

朋友们在使用这一完整代码时需要注意以下要点：

1、自行安装库：pandas、scipy、statsmodels、plotnine

pip install pandas scipy statsmodels plotnine

2、原数据必须为清洁格式，即

①每项观察构成一行

②每个变量构成一列：continuous_var（连续变量，如本示例中的Hb）、categorical_var（分类变量，如本示例中的group）

③每个单元格代表一个值

3、在调用自定义函数one_way_anova(y, x,df,histogram=True)时，一定要注意英文的引号‘’

one_way_anova(y='Hb',x='group', df=df,histogram=True)

连续变量名（Hb）和分类变量名（group）需要添加英文引号，即''

而数据框名（df）则不需要添加英文引号

4、默认参数 histogram=False，即不绘制各组的频数图。

参数 histogram=True则绘制各组的频数图

定义一次函数，以后无数次调用，真正实现统计自动化。