归并排序 图解 递归 + 非递归 + 笔记

前置知识：讲解019-算法笔试中处理输入和输出，讲解020-递归和master公式

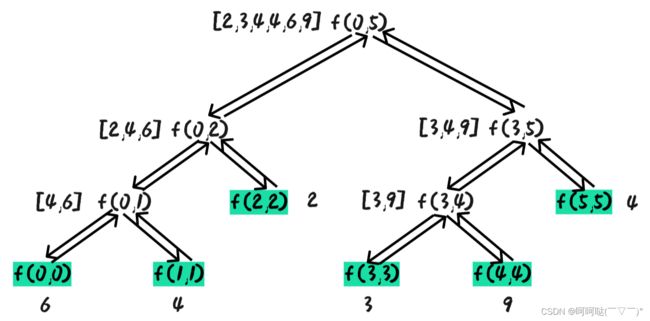
• (1)左部分排好序，右部分排好序，利用merge过程让左右整体有序
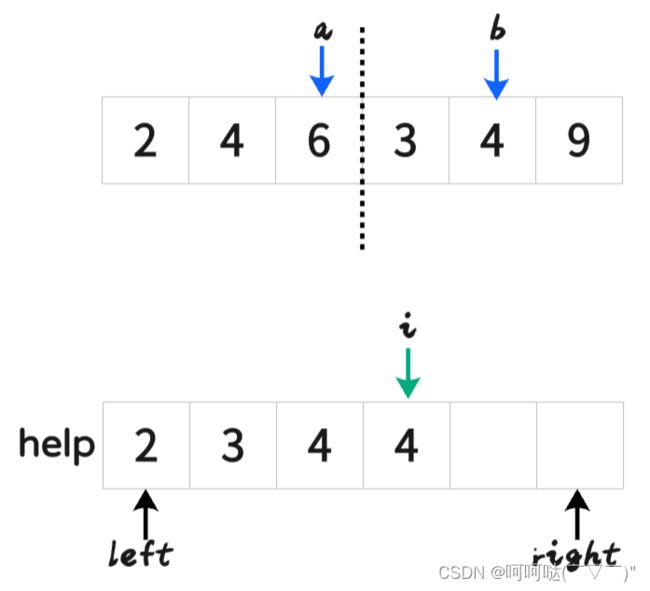
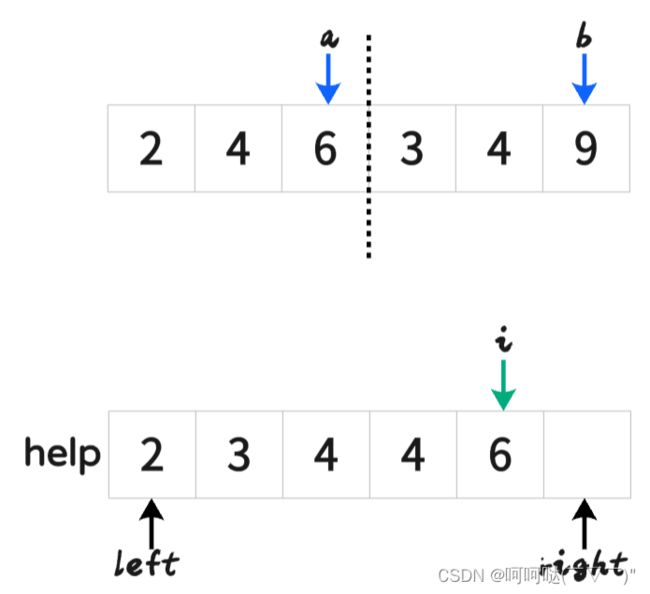
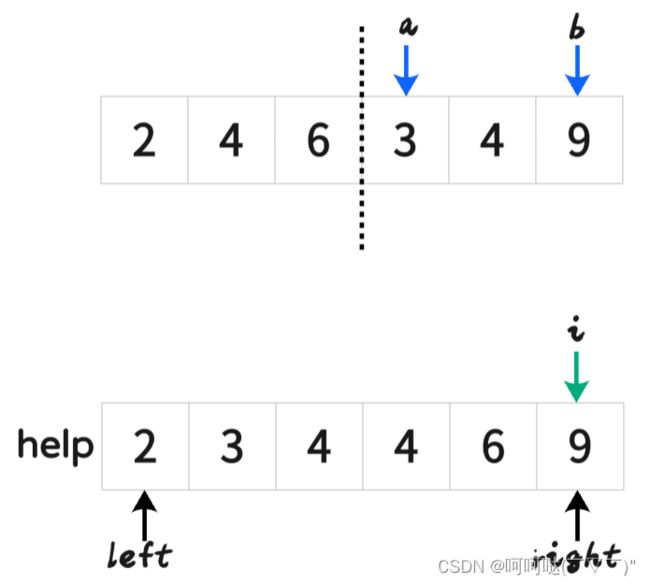
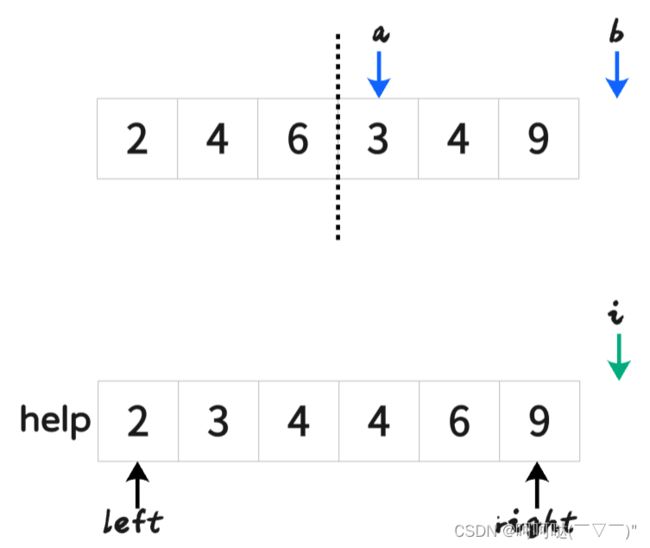
• (2)merge过程:谁小拷贝谁，直到左右两部分所有的数字耗尽
• (3)递归实现和非递归实现
• (4)时间复杂度O(n*logn)
• (5)需要辅助数组，所以额外空间复杂度O(n)
• (6)归并排序为什么比O(n^2)的排序快？因为比较行为没有浪费!
• (7)利用归并排序的便利性可以解决很多问题，例如归并分治

注意:有些资料说可以用原地归并排序，把额外空间复杂度变成O(1)，不要浪费时间去学。因为原地归并排序确实可以省空间，但是会把复杂度变成O(n^2)

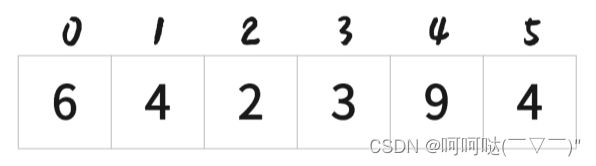
• 对这个数组arr=[6,4,2,3,9,4] ,进行归并排序 

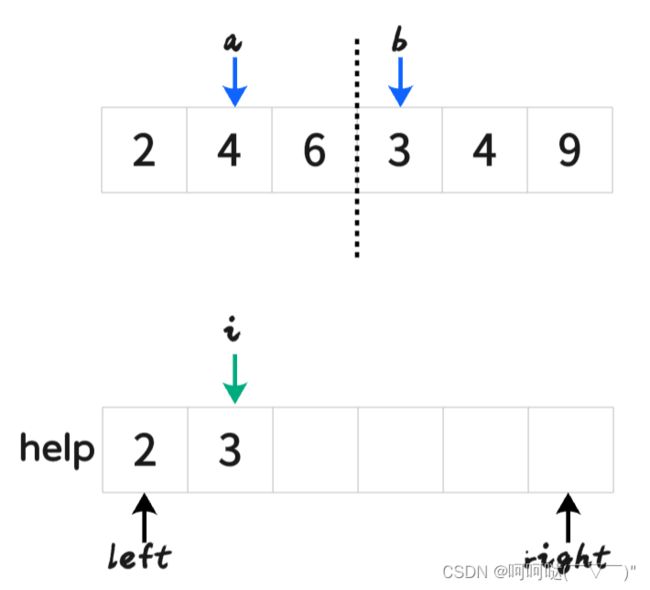
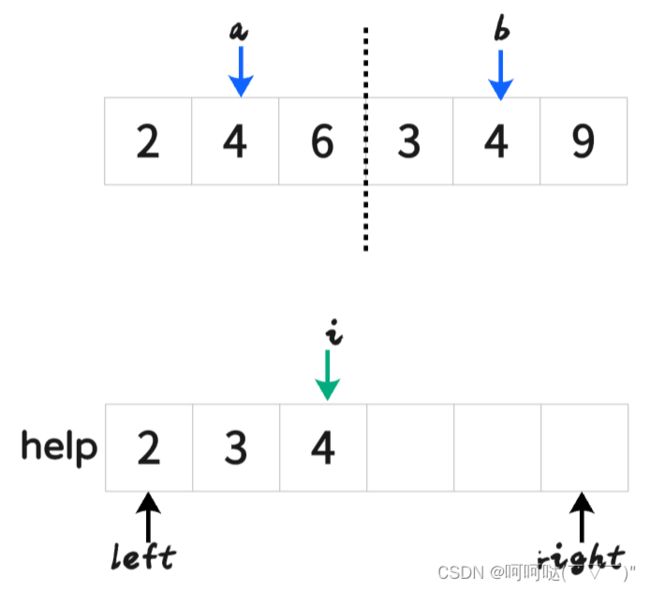
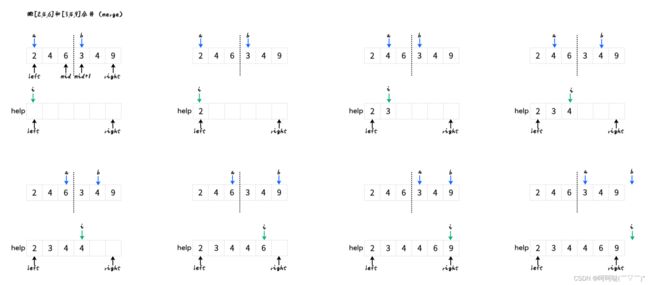
• 挑其中一步来演示： 把[2,4,6]和[3,4,9]合并（merge）

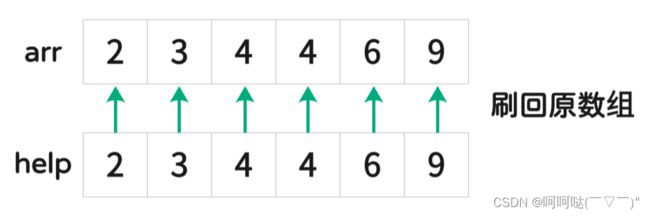
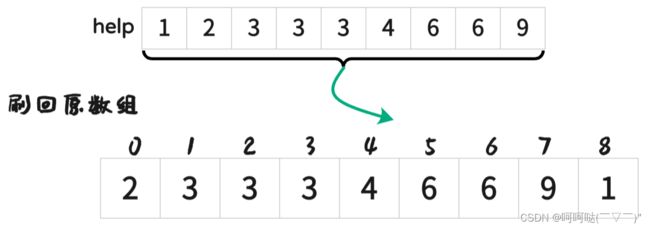
最后再刷回原数组 

void merge(int left, int mid, int right) {
	int i = left;
	int a = left;
	int b = mid + 1;
	while (a <= mid && b <= right) {
		help[i++] = arr[a] <= arr[b] ? arr[a++] : arr[b++];
	}
	// 左侧指针，右侧指针，必有一个越界，另一个不越界
	while (a <= mid) {
		help[i++] = arr[a++];
	}
	while (b <= right) {
		help[i++] = arr[b++];
	}
	for (i = left; i <= right; i++) { // 把 help 里面的数据重新刷回到原数组arr
		arr[i] = help[i];
	}
}

（1）归并排序递归版

// 递归方法
void mergeSort(int left, int right) {
	if (left == right) return;
	int mid = (left + right) / 2;
	mergeSort(left, mid);
	mergeSort(mid + 1, right);
	merge(left, mid, right);
}

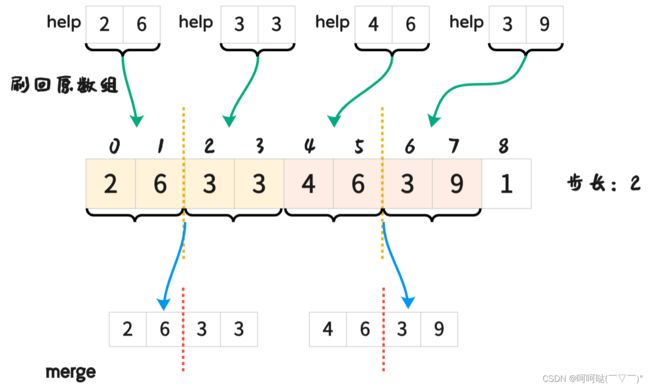
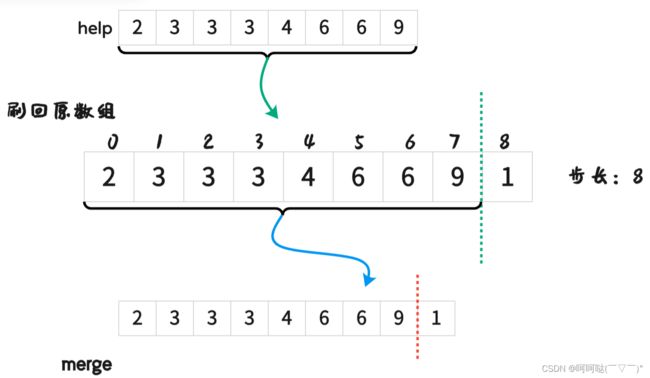
（2）归并排序非递归版

void mergeSort2() {
	// 一共发生O(logn)次
	for (int left, mid, right, step = 1; step < n; step <<= 1) {
		// 内部分组merge，时间复杂度：O(n)
		left = 0;
		while (left < n) {
			mid = left + step - 1;
			if (mid + 1 >= n) {
				// 已经没有右侧了
				break;
			}
			// 有右侧,求右侧的右边界
			right = min(left + (step << 1) - 1, n - 1);
			// left ... mid mid+1 ... right
			//								left ... mid mid+1 ... right
			//															 left ... mid mid+1 ... right
			merge(left, mid, right);
			left = right + 1;
		}
	}	
}

完整代码：

/*
* 前置知识：讲解019-算法笔试中处理输入和输出，讲解020-递归和master公式
	(1)左部分排好序，右部分排好序，利用merge过程让左右整体有序
	(2)merge过程:谁小拷贝谁，直到左右两部分所有的数字耗尽
	(3)递归实现和非递归实现
	(4)时间复杂度O(n*logn)
	(5)需要辅助数组，所以额外空间复杂度O(n)
	(6)归并排序为什么比O(n^2)的排序快？因为比较行为没有浪费!
	(7)利用归并排序的便利性可以解决和诺问题 - 归并分治 - 下节课
	注意:
	有些资料说可以用原地归并排序，把额外空间复杂度变成O(1)，不要浪费时间去学
	因为原地归并排序确实可以省空间，但是会把复杂度变成O(n^2)
	有关排序更多的概念，注意点，闭坑指南，将在后序课程继续
*/
#include 
#include 
#include 
using namespace std;
#include 
#define MAXI 501
int arr[] = { 6,4,2,3,9,4 };
int n = sizeof(arr) / sizeof(arr[0]);
int help[MAXI];

void merge(int left, int mid, int right) {
	int i = left;
	int a = left;
	int b = mid + 1;
	while (a <= mid && b <= right) {
		help[i++] = arr[a] <= arr[b] ? arr[a++] : arr[b++];
	}
	// 左侧指针，右侧指针，必有一个越界，另一个不越界
	while (a <= mid) {
		help[i++] = arr[a++];
	}
	while (b <= right) {
		help[i++] = arr[b++];
	}
	for (i = left; i <= right; i++) { // 把 help 里面的数据重新刷回到原数组arr
		arr[i] = help[i];
	}
}

/*
	归并排序递归版
	假设left...right一共 n 个数
	T(n) = 2 * T(n/2) + O(n)
	a = 2,b = 2,c = 1
	根据master公式，时间复杂度：O(n * logn)
	空间复杂度：O(n)
*/
// 递归方法
void mergeSort(int left, int right) {
	if (left == right) return;
	int mid = (left + right) / 2;
	mergeSort(left, mid);
	mergeSort(mid + 1, right);
	merge(left, mid, right);
}

// 归并排序非递归版
// 时间复杂度：O(n * logn)
// 空间复杂度：O(n)
void mergeSort2() {
	// 一共发生O(logn)次
	for (int left, mid, right, step = 1; step < n; step <<= 1) {
		// 内部分组merge，时间复杂度：O(n)
		left = 0;
		while (left < n) {
			mid = left + step - 1;
			if (mid + 1 >= n) {
				// 已经没有右侧了
				break;
			}
			// 有右侧,求右侧的右边界
			right = min(left + (step << 1) - 1, n - 1);
			// left ... mid mid+1 ... right
			//								left ... mid mid+1 ... right
			//															 left ... mid mid+1 ... right
			merge(left, mid, right);
			left = right + 1;
		}
	}	
}

int main() {
	//mergeSort(0, n - 1);
	mergeSort2();
	for (int i = 0; i < n; i++) {
		cout << " " << arr[i] << " " << endl;
	}
	system("pause");
	return 0;
}

完整图：

参考和推荐视频：

算法讲解021【必备】归并排序_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1wu411p7r7/?spm_id_from=333.999.list.card_archive.click&vd_source=a934d7fc6f47698a29dac90a922ba5a3