【LeetCode】试题总结:深度优先搜索 (DFS)
【LeetCode】试题总结:深度优先搜索 (DFS)
-
- 数据结构:二叉树中的 DFS
-
- (一)、相同的树
- 105. 从前序与中序遍历序列构造二叉树
- 104. 二叉树的最大深度
- 110. 平衡二叉树
- 114. 二叉树展开为链表
- 112. 路径总和
- 113. 路径总和 II
- 方法四、(DFS+回溯)
- 130. 被围绕的区域
说明:本文仅做为本人总结算法竞赛试题的笔记,参照许多了题解,如有侵权请联系。
数据结构:二叉树中的 DFS
(一)、相同的树
试题链接
https://leetcode-cn.com/problems/same-tree/
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if (p == null && q == null) {
return true;
} else if (p == null || q == null) {
return false;
} else if (p.val != q.val) {
return false;
} else {
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
}
}
105. 从前序与中序遍历序列构造二叉树
https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
方法一:递归
思路
对于任意一颗树而言,前序遍历的形式总是
[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是
[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
只要我们在中序遍历中定位到根节点,那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的,因此我们就可以对应到前序遍历的结果中,对上述形式中的所有左右括号进行定位。
这样以来,我们就知道了左子树的前序遍历和中序遍历结果,以及右子树的前序遍历和中序遍历结果,我们就可以递归地对构造出左子树和右子树,再将这两颗子树接到根节点的左右位置。
细节
在中序遍历中对根节点进行定位时,一种简单的方法是直接扫描整个中序遍历的结果并找出根节点,但这样做的时间复杂度较高。我们可以考虑使用哈希表来帮助我们快速地定位根节点。对于哈希映射中的每个键值对,键表示一个元素(节点的值),值表示其在中序遍历中的出现位置。在构造二叉树的过程之前,我们可以对中序遍历的列表进行一遍扫描,就可以构造出这个哈希映射。在此后构造二叉树的过程中,我们就只需要 O(1)O(1)O(1) 的时间对根节点进行定位了。
下面的代码给出了详细的注释。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
// dfs 递归
class Solution {
private Map<Integer, Integer> indexMap;
public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if (preorder_left > preorder_right) {
return null;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = indexMap.get(preorder[preorder_root]);
// 先把根节点建立出来
TreeNode root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
int n = preorder.length;
// 构造哈希映射,帮助我们快速定位根节点
indexMap = new HashMap<Integer, Integer>();
for (int i = 0; i < n; i++) {
indexMap.put(inorder[i], i);
}
return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}
}
class Solution {
private Map<Integer, Integer> indexMap;
public TreeNode myBuildTree(int[] preorder, int[] inorder, int pr
复杂度分析
时间复杂度:O(n)O(n)O(n),其中 nnn 是树中的节点个数。
空间复杂度:O(n)O(n)O(n),除去返回的答案需要的 O(n)O(n)O(n) 空间之外,我们还需要使用 O(n)O(n)O(n) 的空间存储哈希映射,以及 O(h)O(h)O(h)(其中 hhh 是树的高度)的空间表示递归时栈空间。这里 h<nh < nh<n,所以总空间复杂度为 O(n)O(n)O(n)。
方法二:迭代
思路
迭代法是一种非常巧妙的实现方法。
对于前序遍历中的任意两个连续节点 uuu 和 vvv,根据前序遍历的流程,我们可以知道 uuu 和 vvv 只有两种可能的关系:
### 108. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
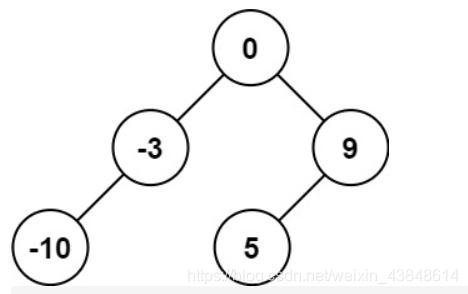
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
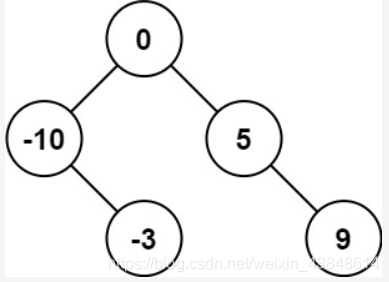
前序遍历
```java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return helper(nums, 0, nums.length - 1);
}
public TreeNode helper(int[] nums, int left, int right) {
if (left > right) {
return null;
}
// 总是选择中间位置左边的数字作为根节点
int mid = (left + right) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = helper(nums, left, mid - 1);
root.right = helper(nums, mid + 1, right);
return root;
}
}
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
class Solution {
public int maxDepth(TreeNode root) {
if (root == null){
return 0;
}else{
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
}
}
110. 平衡二叉树
https://leetcode-cn.com/problems/balanced-binary-tree/
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
输入:root = [3,9,20,null,null,15,7]
输出:true
自己写的报错:
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null){
return true;
}else{
return Math.abs( height(root.right)- height(root.left)) <= 1;
}
}
public int height(TreeNode root){
if (root == null){
return 0;
}else{
return Math.max(height(root.left), height(root.right))+1;
}
}
}
输入:
[1,2,2,3,null,null,3,4,null,null,4]
输出:
true
预期结果:
false
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
} else {
return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
}
public int height(TreeNode root) {
if (root == null) {
return 0;
} else {
return Math.max(height(root.left), height(root.right)) + 1;
}
}
}
查错:
return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
方法一:自顶向下的递归
定义函数 height,用于计算二叉树中的任意一个节点 p 的高度:
有了计算节点高度的函数,即可判断二叉树是否平衡。具体做法类似于二叉树的前序遍历,即对于当前遍历到的节点,首先计算左右子树的高度,如果左右子树的高度差是否不超过 1,再分别递归地遍历左右子节点,并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
class Solution {
public void flatten(TreeNode root) {
if (root == null){
return ;
}
flatten(root.left);
TreeNode tem = root.right;
root.right = root.left;
root.left = null;
while (root.right != null) {
root = root.right;
}
flatten(tem);
root.right = tem;
}
}
112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum ,判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
叶子节点 是指没有子节点的节点。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
class Solution {
public boolean hasPathSum(TreeNode root, int sum) {
if (root == null) {
return false;
}
if (root.left == null && root.right == null) {
return sum == root.val;
}
return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
}
}
BFS:
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null){
return false;
}
Queue<TreeNode> queueNode = new LinkedList();
Queue<Integer> queueSumValue = new LinkedList();
queueNode.offer(root);
queueSumValue.offer(root.val);
while(!queueNode.isEmpty()){
int levelNums = queueNode.size();
for (int i = 0; i < levelNums; i++){
TreeNode temNode = queueNode.poll();
int temNum = queueSumValue.poll();//temNode.val;
if (temNum == targetSum && temNode.left == null && temNode.right == null){
return true;
}
if (temNode.left != null){
queueNode.offer(temNode.left);
queueSumValue.offer(temNode.left.val+temNum);
}
if (temNode.right != null){
queueNode.offer(temNode.right);
queueSumValue.offer(temNode.right.val+temNum);
}
}
}
return false;
}
}
113. 路径总和 II
https://leetcode-cn.com/problems/path-sum-ii/
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
注意到本题的要求是,找到所有满足从「根节点」到某个「叶子节点」经过的路径上的节点之和等于目标和的路径。核心思想是对树进行一次遍历,在遍历时记录从根节点到当前节点的路径和,以防止重复计算。
方法一:深度优先搜索
思路及算法
我们可以采用深度优先搜索的方式,枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
代码
class Solution {
List<List<Integer>> ret = new LinkedList<List<Integer>>();
Deque<Integer> path = new LinkedList<Integer>();
public List<List<Integer>> pathSum(TreeNode root, int sum) {
dfs(root, sum);
return ret;
}
public void dfs(TreeNode root, int sum) {
if (root == null) {
return;
}
path.offerLast(root.val);
sum -= root.val;
if (root.left == null && root.right == null && sum == 0) {
ret.add(new LinkedList<Integer>(path));
}
dfs(root.left, sum);
dfs(root.right, sum);
path.pollLast();
}
}
复杂度分析
时间复杂度:O(N2)O(N^2)O(N2),其中 NNN 是树的节点数。在最坏情况下,树的上半部分为链状,下半部分为完全二叉树,并且从根节点到每一个叶子节点的路径都符合题目要求。此时,路径的数目为 O(N)O(N)O(N),并且每一条路径的节点个数也为 O(N)O(N)O(N),因此要将这些路径全部添加进答案中,时间复杂度为 O(N2)O(N^2)O(N2)。
空间复杂度:O(N)O(N)O(N),其中 NNN 是树的节点数。空间复杂度主要取决于栈空间的开销,栈中的元素个数不会超过树的节点数。
方法二:广度优先搜索
思路及算法
我们也可以采用广度优先搜索的方式,遍历这棵树。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
为了节省空间,我们使用哈希表记录树中的每一个节点的父节点。每次找到一个满足条件的节点,我们就从该节点出发不断向父节点迭代,即可还原出从根节点到当前节点的路径。
代码
class Solution {
List<List<Integer>> ret = new LinkedList<List<Integer>>();
Map<TreeNode, TreeNode> map = new HashMap<TreeNode, TreeNode>();
public List<List<Integer>> pathSum(TreeNode root, int sum) {
if (root == null) {
return ret;
}
Queue<TreeNode> queueNode = new LinkedList<TreeNode>();
Queue<Integer> queueSum = new LinkedList<Integer>();
queueNode.offer(root);
queueSum.offer(0);
while (!queueNode.isEmpty()) {
TreeNode node = queueNode.poll();
int rec = queueSum.poll() + node.val;
if (node.left == null && node.right == null) {
if (rec == sum) {
getPath(node);
}
} else {
if (node.left != null) {
map.put(node.left, node);
queueNode.offer(node.left);
queueSum.offer(rec);
}
if (node.right != null) {
map.put(node.right, node);
queueNode.offer(node.right);
queueSum.offer(rec);
}
}
}
return ret;
}
public void getPath(TreeNode node) {
List<Integer> temp = new LinkedList<Integer>();
while (node != null) {
temp.add(node.val);
node = map.get(node);
}
Collections.reverse(temp);
ret.add(new LinkedList<Integer>(temp));
}
}
复杂度分析
时间复杂度: O ( N 2 ) O(N^2) O(N2),其中 NNN 是树的节点数。分析思路与方法一相同。
空间复杂度:O(N),其中 NNN 是树的节点数。空间复杂度主要取决于哈希表和队列空间的开销,哈希表需要存储除根节点外的每个节点的父节点,队列中的元素个数不会超过树的节点数。
方法四、(DFS+回溯)
https://leetcode-cn.com/problems/path-sum-ii/solution/hui-su-suan-fa-shen-du-you-xian-bian-li-zhuang-tai/
问完成一件事情的所有解决方案,一般采用回溯算法(深度优先遍历)完成。
回溯算法问题一般先画图,好在这就是一个树形问题,题目已经给我们画好了示意图。
根据这个问题的特点,我们可以采用 先序遍历 的方式:先使用 sum 减去当前结点(如果非空)的值,然后再递归处理左子树和右子树。如果到了叶子结点,sum 恰好等于叶子结点的值,我们就得到了一个符合条件的列表(从根结点到当前叶子结点的路径)。
归纳一下递归终止条件:
- 如果遍历到的结点为空结点,返回;
- 如果遍历到的叶子结点,且 sum 恰好等于叶子结点的值。
下面是和 @ohenry 讨论出来的 3 种写法,实际上都是一样的,区别仅仅在于一些细节上的处理,它们是:在当前结点非空的前提下,是否先减去当前结点的值,是否先把当前结点的值加入 path ,再判断递归终止条件,再递归调用。
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class Solution {
public List<List<Integer>> pathSum(TreeNode root, int sum) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
// Java 文档中 Stack 类建议使用 Deque 代替 Stack,注意:只使用栈的相关接口
Deque<Integer> path = new ArrayDeque<>();
dfs(root, sum, path, res);
return res;
}
private void dfs(TreeNode node, int sum, Deque<Integer> path, List<List<Integer>> res) {
// 递归终止条件 1
if (node == null) {
return;
}
// 递归终止条件 2
if (node.val == sum && node.left == null && node.right == null) {
// 当前结点的值还没添加到列表中,所以要先添加,然后再移除
path.addLast(node.val);
res.add(new ArrayList<>(path));
path.removeLast();
return;
}
path.addLast(node.val);
dfs(node.left, sum - node.val, path, res);
// 进入左右分支的 path 是一样的,这里不用写下面两行,因为一定会调用到 path.removeLast();
// path.removeLast();
// path.addLast(node.val);
dfs(node.right, sum - node.val, path, res);
path.removeLast();
}
}
这里的状态是指完成一件事情进行到哪一个阶段,在上面的代码中:path 、sum 都是状态变量,sum 发生的行为是复制,所以无需重置,path 全程只有一份,因此在深度优先遍历从深层回到浅层以后,需要重置。
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> result = new ArrayList<>();
dfs (root, targetSum, new ArrayList<Integer>(), result);
return result;
}
public void dfs(TreeNode root, int sum, List<Integer> list, List<List<Integer>> result){
if (root == null){
return;
}
list.add(new Integer(root.val));
if (root.left == null && root.right == null){
if (sum == root.val){
result.add(new ArrayList(list));
}
list.remove(list.size()-1);
return;
}
sum = sum - root.val;
dfs(root.left, sum, list, result);
dfs(root.right, sum, list, result);
list.remove(list.size()-1);
}
}
130. 被围绕的区域
原题链接:
https://leetcode-cn.com/problems/surrounded-regions/
给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。
输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
class Solution {
int m,n;
public void solve(char[][] board) {
m = board.length;// the num of row;
n = board[0].length; // the num of column;
// 左右边界搜索
for (int i = 0; i < m; i++){
dfs(board, i, 0);
dfs(board, i, n-1);
}
// 上下边界搜索
for (int i = 0; i < n; i++){
dfs(board, 0, i);
dfs(board, m-1, i);
}
for (int i = 0; i < m; i++){
for (int j = 0; j < n; j++){
if (board[i][j] == 'O'){
board[i][j] = 'X';
}else if (board[i][j] == 'A') {
board[i][j] = 'O';
}
}
}
}
public void dfs(char[][] board, int x, int y){
if (x<0 || x>=m || y<0 || y>=n || board[x][y] != 'O'){
return;
}else{
board[x][y] = 'A';
dfs(board, x + 1, y);//上
dfs(board, x - 1, y);
dfs(board, x, y + 1);
dfs(board, x, y - 1);
}
}
}
https://leetcode-cn.com/problems/number-of-islands/solution/dao-yu-lei-wen-ti-de-tong-yong-jie-fa-dfs-bian-li-/
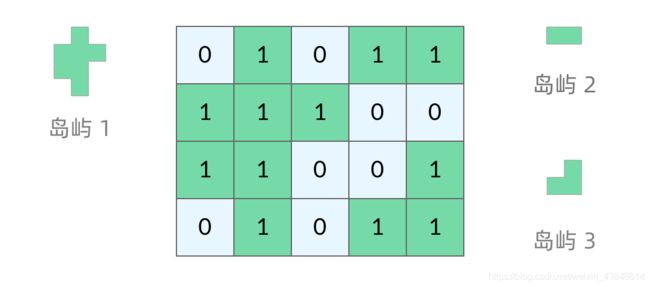
在 LeetCode 中,「岛屿问题」是一个系列系列问题,比如:
L200. 岛屿数量 (Easy)
463. 岛屿的周长 (Easy)
695. 岛屿的最大面积 (Medium)
827. 最大人工岛 (Hard)
作者:nettee
链接:https://leetcode-cn.com/problems/number-of-islands/solution/dao-yu-lei-wen-ti-de-tong-yong-jie-fa-dfs-bian-li-/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题是这类网格 DFS 问题的典型代表。网格结构遍历起来要比二叉树复杂一些,如果没有掌握一定的方法,DFS 代码容易写得冗长繁杂。
本文将以岛屿问题为例,展示网格类问题 DFS 通用思路,以及如何让代码变得简洁。
网格类问题的 DFS 遍历方法
网格问题的基本概念
我们首先明确一下岛屿问题中的网格结构是如何定义的,以方便我们后面的讨论。
网格问题是由 m×nm \times nm×n 个小方格组成一个网格,每个小方格与其上下左右四个方格认为是相邻的,要在这样的网格上进行某种搜索。
岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。我们把数字为 0 的格子看成海洋格子,数字为 1 的格子看成陆地格子,这样相邻的陆地格子就连接成一个岛屿。
在这样一个设定下,就出现了各种岛屿问题的变种,包括岛屿的数量、面积、周长等。不过这些问题,基本都可以用 DFS 遍历来解决。
DFS 的基本结构
网格结构要比二叉树结构稍微复杂一些,它其实是一种简化版的图结构。要写好网格上的 DFS 遍历,我们首先要理解二叉树上的 DFS 遍历方法,再类比写出网格结构上的 DFS 遍历。我们写的二叉树 DFS 遍历一般是这样的:
void traverse(TreeNode root) {
// 判断 base case
if (root == null) {
return;
}
// 访问两个相邻结点:左子结点、右子结点
traverse(root.left);
traverse(root.right);
}