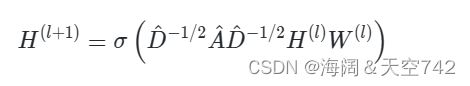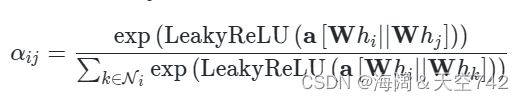实战-----基于 PyTorch 的 GNN 搭建

目录

1.图的表示

2.图卷积网络（GCN）的搭建

3.图注意力网络（GAT）的搭建

4.PyG 基础：图数据的操作

1.torch_geometric 的安装

2.图数据的属性

3.基准图数据库及基本操作

4.图数据的可视化

5.实验总结

1.图的表示

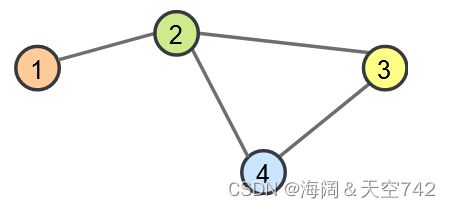
    在开始讨论特定的图神经网络操作之前，我们首先来考虑如何表示图。在数学上，图 G 定义为一组节点/顶点 V 和一组边/链接 E：G=（V，E） 的二元组。每条边链接两个顶点，如下图所示：

                        

如上图所示，顶点是 V=1,2,3,4，边是 E=（1,2）、（2,3）、（2,4）、（3,4）。注意，这里为了简单起见，假设图是无向的，因此不添加像 （2,1）（2,1） 这样的镜像对。在实际应用中，顶点和边通常可以具有特定的属性特征，也可以是有向边。那么，如何用一种有效的方法来表示图呢？通常有两种方案：

• 邻接矩阵：表示顶点之间相邻关系的矩阵。
• 邻接表：存储方法跟树的孩子链表示法相类似，是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点，则把相邻顶点依次存放于表头结点所指向的单向链表中。

2.图卷积网络（GCN）的搭建

     图卷积神经网络（Graph Convolutional networks, GCN）由 Kipf 等人在 2016 年提出，类似于图像中的卷积处理，CNN 中的卷积本质上就是利用共享参数的过滤器，通过计算中心像素点以及相邻像素点的加权和来实现空间特征的提取。而 GCN 也是如此，依赖于节点间的消息传递方法，这意味着点与其邻居点交换信息，并相互发送消息。在看具体的数学表达式之前，我们可以试着直观地理解 GCN 是如何工作的，可分为以下两大步骤：

    第一步，每个节点创建一个特征向量，表示它要发送给所有邻居的消息。

    第二步，消息被发送到相邻节点，这样每个节点均会从其相邻节点接收一条消息。

下面的图可视化了以上两大步骤：

之后，如何组合节点   接收的所有消息呢？由于节点间消息的数量不同，因此需要一个适用于任意数量的操作，通常的方法是求和或取平均值。令  表示节点 以前的特征表示， 为整合消息后的特征表示，GCN 层定义如下:

                       

     是将输入特征转换为消息的权重参数。在邻接矩阵 A 的基础上，加上单位矩阵，以便每个节点也向自身发送消息，即：A^=A+I。最后，为了取平均值的运算，需要用到矩阵 D^，这是一个对角矩阵，Dii 表示节点 i 的邻居数。σ 表示一个任意的激活函数，当然，不一定是 Sigmoid，事实上，在 GNN 中通常使用基于 ReLU 的激活函数。

       在 PyTorch 中实现 GCN 层时，我们可以灵活地利用张量进行运算，不必定义矩阵 D^，只需将求和的消息除以之后的邻居数即可。此外，线性层便是以上的权重矩阵，同时可以添加 bias。基于 PyTorch，GCN 层可定义如下：

import torch
import torch.nn as nn

class GCNLayer(nn.Module):

    def __init__(self,c_in,c_out):
        """
        Inputs:
        :param c_in: 输入特征
        :param c_out: 输出特征
        """
        super().__init__()
        self.projection = nn.Linear(c_in,c_out); #线性层
        
    def forword(self,node_feats,adj_matrix):
        """
        输入
        :param node_feats: 节点特征表示，大小为[batch_size,num_nodes,c_in]
        :param adj_matrix: 邻接矩阵：[batch_size,num_nodes,num_nodes]
        :return:
        """
        num_neighbors = adj_matrix.sum(dim=-1,keepdims=True)#各节点的邻居数
        node_feats = self.projection(node_feats)#将特征转化为消息
        #各邻居节点消息求和并求平均
        node_feats = torch.bmm(adj_matrix,node_feats)
        node_feats = node_feats / num_neighbors
        return node_feats

       为了进一步理解 GCN 层，可将其应用至上面的节点示例图中。首先，基于上面示例图，指定一些节点特征和添加自连接的邻接矩阵 ：

node_feats = torch.arange(8,
dtype=torch.float32).view(1,4,2)
adj_matrix = torch.Tensor([[[1,1,0,0],
            [1,1,1,1],
            [0,1,1,1],
            [0,1,1,1]]])
print("节点特征：\n",node_feats)
print("添加自链接的邻接矩阵：\n",adj_matrix)

       接下来将其输入 GCN 层，为简单起见，这里将线性权重矩阵初始化为单位矩阵，以便输入特征与消息相等，可以更容易地验证消息传递操作。

layer = GCNLayer(c_in=2, c_out=2)
# 初始化权重矩阵
layer.projection.weight.data = torch.Tensor([[1., 0.], [0., 1.]])
layer.projection.bias.data = torch.Tensor([0., 0.])

# 将节点特征和添加自连接的邻接矩阵输入 GCN 层
with torch.no_grad():
    out_feats = layer(node_feats, adj_matrix)

print("节点特征:\n", node_feats)
print("添加自连接的邻接矩阵:\n", adj_matrix)
print("节点输出特征:\n", out_feats)

结果：

节点特征：
 tensor([[[0., 1.],
         [2., 3.],
         [4., 5.],
         [6., 7.]]])
添加自链接的邻接矩阵：
 tensor([[[1., 1., 0., 0.],
         [1., 1., 1., 1.],
         [0., 1., 1., 1.],
         [0., 1., 1., 1.]]])
节点输出特征：
 tensor([[[1., 2.],
         [3., 4.],
         [4., 5.],
         [4., 5.]]])

Process finished with exit code 0

        如上所见，第一个节点的输出值是其自身和第二个节点的平均值，其他节点同理。当然，在具体实践中，我们还希望允许节点之间的消息传递不仅仅局限于邻居节点，这可以通过应用多个 GCN 层来实现，而很多的 GNN 即是由多个 GCN 和非线性（如 ReLU）的组合构建而成，如下图所示：

                 

     通过以上 GCN 层的运算示例，发现一个问题，即节点 3 和 4 的输出相同，这是因为它们具有相同的相邻节点（包括自身）输入，再取均值，所得到的值便一样了。这在大部分情况下并不合理。

3.图注意力网络（GAT）的搭建

   为了解决此问题，一种常见的方法是对自连接添加更高的权重，或者为不同连接定义不同的权重，这里就涉及到了另一个重要概念：注意力机制。

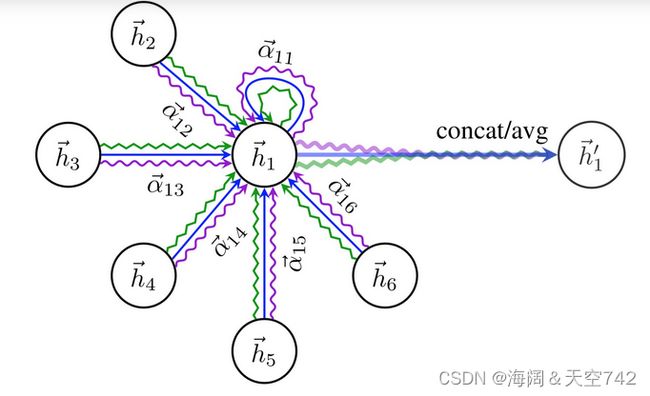
   注意力机制描述了多个元素的加权平均，这一概念同样适用于图，称为图注意力网络（Graph Attention Networks，GAT，由 Velickovic et al.，2017 提出)，与 GCN 类似，图注意力层使用线性层为每个节点创建消息。对于注意力的计算部分，综合使用来自节点本身的特征以及其它节点的特征。节点从 i 到 j 的最终注意力权重 αij​ 的计算示意图如下所示：

                  

    hi​ 和 hj​ 分别是节点 i 和 j 的原始特征，用 W 作为权重矩阵，运算后进行拼接，再经过权重矩阵 a 的计算，其形状为 [1,2×dmessage​]，接着经由激活函数（例如 LeakyReLU）以及 Softmax 的运算，最后计算而得的 αij​ 表示节点从 i 到 j 的最终注意力权重，计算方法如下：

                   

   最终的节点特征值 hi′​ 基于所有 αij​ 以及相应的 Whj​ 进行加权平均而得,σ 表示激活函数,示意图如下：

                      

   为了增加图注意力网络的表征能力，Velickovic 等人建议将其扩展到多头机制，类似于 Transformer 中的多头注意力模块。在有了对图注意层的基本了解之后，我们可以基于 PyTorch 实现它：

import torch
import torch.nn as nn
import torch.nn.functional as F

class GATLayer(nn.Module):

    def __int__(self,c_in,c_out,
                num_heads=1,concat_heads=True,alpha=0.2):
        """

        :param c_in: 输入特征维度
        :param c_out: 输出特征维度
        :param num_heads: 多头的数量
        :param concat_heads: 是否拼接多头计算的结果
        :param alpha: LeakyReLU的参数
        :return:
        """
        super().__init__()
        self.num_heads = num_heads
        self.concat_heads = num_heads
        if self.concat_heads:
            assert c_out % num_heads ==0,"输出特征数必须是头数的倍数！"
            c_out = c_out // num_heads

        #参数
        self.projection = nn.Linear(c_in,c_out*num_heads) #有几个头，就需要将c_out扩充几倍
        self.a = nn.Parameter(torch.Tensor(num_heads,2*c_out)) #用于计算注意力的参数，由于对两节点拼接后的向量进行操作，所以2*c_out
        self.leakrelu = nn.LeakyReLU(alpha) #激活层

        #参数初始化
        nn.init.xavier_uniform_(self.projection.weight.data, gain=1.414)
        nn.init.xavier_uniform_(self.a.data, gain=1.414)

        def forward(self,node_feats,adj_matrix,print_attn_probs=False):
            """
            输入：
            :param self:
            :param node_feats: 节点的特征表示
            :param adj_matrix: 邻接矩阵
            :param print_attn_probs: 是否打印注意力
            :return:
            """
            batch_size,num_nodes = node_feats.size(0),node_feats.size(1)

            #将节点初始输入进行权重运算
            node_feats = self.projection(node_feats)
            #扩展出多头数量的维度
            node_feats = node_feats.view(batch_size,num_nodes,self.num_heads,-1)

            # 获取所有顶点对拼接而成的特征向量 a_input
            edges = adj_matrix.nonzero(as_tuple=False)  # 返回所有邻接矩阵中值不为 0 的 index，即所有连接的边对应的两个顶点
            node_feats_flat = node_feats.view(batch_size * num_nodes, self.num_heads, -1)  # 将所有 batch_size 的节点拼接

            edge_indices_row = edges[:, 0] * batch_size + edges[:, 1]  # 获取边对应的第一个顶点 index
            edge_indices_col = edges[:, 0] * batch_size + edges[:, 2]  # 获取边对应的第二个顶点 index

            a_input = torch.cat([
            torch.index_select(input=node_feats_flat, index=edge_indices_row, dim=0), # 基于边对应的第一个顶点的 index 获取其特征值
                torch.index_select(input=node_feats_flat, index=edge_indices_col, dim=0)  # 基于边对应的第二个顶点的 index 获取其特征值
            ], dim=-1)  # 两者拼接

            # 基于权重 a 进行注意力计算
            attn_logits = torch.einsum('bhc,hc->bh', a_input, self.a)
            # LeakyReLU 计算
            attn_logits = self.leakyrelu(attn_logits)

            # 将注意力权转换为矩阵的形式
            attn_matrix = attn_logits.new_zeros(adj_matrix.shape + (self.num_heads,)).fill_(-9e15)
            attn_matrix[adj_matrix[..., None].repeat(1, 1, 1, self.num_heads) == 1] = attn_logits.reshape(-1)

            # Softmax 计算转换为概率
            attn_probs = F.softmax(attn_matrix, dim=2)
            if print_attn_probs:
                print("注意力权重:\n", attn_probs.permute(0, 3, 1, 2))
            # 对每个节点进行注意力加权相加的计算
            node_feats = torch.einsum('bijh,bjhc->bihc', attn_probs, node_feats)

            # 根据是否将多头的计算结果拼接与否进行不同操作
            if self.concat_heads:  # 拼接
                node_feats = node_feats.reshape(batch_size, num_nodes, -1)
            else:  # 平均
                node_feats = node_feats.mean(dim=2)

            return node_feats 

    和前面一样，输入层被初始化为一个单位矩阵，但是我们将 a 设置为任意数字的向量，以获得不同的注意力值。另外，多头机制设置为用两个头：

layer = GATLayer(2, 2, num_heads=2)
layer.projection.weight.data = torch.Tensor([[1., 0.], [0., 1.]])
layer.projection.bias.data = torch.Tensor([0., 0.])
layer.a.data = torch.Tensor([[-0.2, 0.3], [0.1, -0.1]])
node_feats = torch.arange(8, dtype=torch.float32).view(1, 4, 2)
adj_matrix = torch.Tensor([[[1, 1, 0, 0],
                                    [1, 1, 1, 1],
                                    [0, 1, 1, 1],
                                    [0, 1, 1, 1]]])
with torch.no_grad():
    out_feats = layer(node_feats, adj_matrix, print_attn_probs=True)


print("节点特征:\n", node_feats)
print("添加自连接的邻接矩阵:\n", adj_matrix)
print("节点输出特征:\n", out_feats)

注意力权重:
 tensor([[[[0.3543, 0.6457, 0.0000, 0.0000],
          [0.1096, 0.1450, 0.2642, 0.4813],
          [0.0000, 0.1858, 0.2885, 0.5257],
          [0.0000, 0.2391, 0.2696, 0.4913]],

         [[0.5100, 0.4900, 0.0000, 0.0000],
          [0.2975, 0.2436, 0.2340, 0.2249],
          [0.0000, 0.3838, 0.3142, 0.3019],
          [0.0000, 0.4018, 0.3289, 0.2693]]]])
节点特征:
 tensor([[[0., 1.],
         [2., 3.],
         [4., 5.],
         [6., 7.]]])
添加自连接的邻接矩阵:
 tensor([[[1., 1., 0., 0.],
         [1., 1., 1., 1.],
         [0., 1., 1., 1.],
         [0., 1., 1., 1.]]])
节点输出特征:
 tensor([[[1.2913, 1.9800],
         [4.2344, 3.7725],
         [4.6798, 4.8362],
         [4.5043, 4.7351]]])

Process finished with exit code 0

4.PyG 基础：图数据的操作

1.torch_geometric 的安装

     安装torch-geometric之前，需要先安装torch-scatter、torch-sparse、torch-cluster、torch-spline-conv

 安装网址：网址在此

 最后 pip install torch-geometric

安装完成以后，我们可以基于 Data 类构建图数据，比如下图所示的图数据：

                            

2.图数据的属性

简单地说，图构由节点以及边构成，当然在此基础上，还包含一系列其它信息，比如是否有向，是否有孤立点，节点的特征表示等。应用 PyG 中的类 torch_geometric.data.Data，可快速构建你的图数据对象，一般情况下，包含以下默认属性（并非必须属性）：

• data.x: 节点的特征矩阵，大小为 [num_nodes, num_node_features]。
• data.edge_index: 图中的边，以 COO （把矩阵中不为 0 的数的行号，列号存储下来）方式存储，大小为 [2, num_edges]。
• data.edge_attr: 边的特征矩阵，大小为 [num_edges, num_edge_features]。
• data.y: 数据的目标输出, 大小不固定，比如，node-level 的目标输出大小为 [num_nodes, *]，graph-level 的目标输出大小为 [1, *]。
• data.pos:节点的位置矩阵，大小为 [num_nodes, num_dimensions]。

import torch
from torch_geometric.data import Data
# 基于节点的index表示边
#[0,1,1,2]表示出发的节点index
#[1,0,2,1]表示到达index
edge_index = torch.tensor([[0,1,1,2],
                           [1,0,2,1]],dtype=torch.long)
x = torch.tensor([[-1],[0],[1]],dtype=torch.float)#节点的特征矩阵，有3个节点，特征维度为1

data = Data(x=x,edge_index = edge_index) #初始化图
print(data)#查看图属性

结果： 

Data(x=[3, 1], edge_index=[2, 4])

Process finished with exit code 0

edge_index 为边表示矩阵大小，x 为节点的特征矩阵大小。

Data 类还提供如下的一些功能，以获取更多的信息：

获取属性键：

获取某键下的值：

获取节点数：

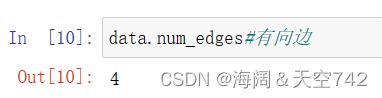
获取边数：

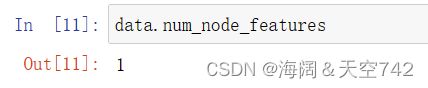
获取节点的特征维度：

查看是否存在孤立的节点：

data.contains_self_loops()

查看是否存在环:

查看是否是有向图：

3.基准图数据库及基本操作

除了可以自定义图数据，PyG 还包含有很多常见的基准数据集，典型代表有：

• Cora：一个根据科学论文之间相互引用关系而构建的图数据集合，论文分为 7 类：Genetic_Algorithms，Neural_Networks，Probabilistic_Methods，Reinforcement_Learning，Rule_Learning，Theory，共 2708 篇。
• Citeseer：一个论文之间引用信息数据集，论文分为 6 类：Agents、AI、DB、IR、ML 和 HCI，共包含 3312 篇论文。
• Pubmed：生物医学方面的论文搜寻以及摘要数据集。

此外，还包含了一系列 3D 点云数据集，比如 FAUST，ShapeNet 等。PyG 提供了这些数据的自动下载，并将其处理成 Data 类的形式，接下来以 ENZYMES 数据集为例（包含 600 个图和 6 个类别）进行说明。

    遗憾的是，在使用 datasets 进行数据集 ENZYMES 的创建时，由于网络不稳定等原因经常会出现 HttpError 类的错误，所以需要手动下载数据集并且注释掉源码中的基于 url 的下载操作，如果你在个人环境中操作，具体步骤如下:

• 第一步：在 url 链接中手动下载数据集：https://www.chrsmrrs.com/graphkerneldatsets/ENZYMES.zip

• 第二步：解压下载的 zip 文件，并构建文件路径：

• - ENZYMES
      - processed # 空文件，后续会存放处理后的数据
      - raw # 存放解压后的几个文件

• 第三步：进入 PyTorch Geometric 库中的 tu_dataset.py 文件（可通过代码 from torch_geometric.datasets import TUDataset 中的 TUDataset 跳转），跳转至类 TUDataset(InMemoryDataset) 后，注释掉其中的 download() 函数，即不基于 url 下载数据集。

接下来拿ENZYMES数据集（包含600个图，每个图分为6个类别，图级别的分类）举例如何使用PyG的公共数据集

from torch_geometric.datasets import TUDataset

# 导入数据集
dataset = TUDataset(
    # 指定数据集的存储位置
    # 如果指定位置没有相应的数据集
    # PyG会自动下载
    root='ENZYMES/',
    # 要使用的数据集
    name='ENZYMES',
)
# 数据集的长度
print(len(dataset))
# 数据集的类别数
print(dataset.num_classes)
# 数据集中节点属性向量的维度
print(dataset.num_node_features)
# 600个图，我们可以根据索引选择要使用哪个图
data = dataset[100]
print(data)
# 随机打乱数据集
dataset = dataset.shuffle()

在导入数据集的时候遇到了一个报错：

AttributeError: module ‘torch‘ has no attribute ‘sparse_csc‘

通过查找网上资料，发现是因为torch-geometric版本过高，通过降低版本，最终解决。参见这篇博客，亲测有效解决方案。

结果如下：

600
6
3
Data(edge_index=[2, 176], x=[45, 3], y=[1])
True

综合以上操作的输出结果，可知此图（dataset[100]）中包含了 45 个节点，特征大小为 3，存在 176/2 = 88 条边，目标标签为 graph-level 的类别（类别标签为 1）。

神经网络通常以批次化的方式进行训练（即基于一小批数据用作一次参数的迭代更新），而 PyG 通过创建稀疏的邻接矩阵，也提供了相应功能的迭代器 DataLoader，加载 torch_geometric.data.DataLoader，可以快速实现数据的批次化。

from torch_geometric.data import DataLoader
loader = DataLoader(dataset, batch_size=32, shuffle=True) # 批次大小为 32，并且数据的顺序随机打乱

批次化迭代：

for batch in loader:
    print("一批数据：",batch)
    print("一批数据量：",batch.num_graphs)

结果如下：

一批数据： DataBatch(edge_index=[2, 4000], x=[1026, 3], y=[32], batch=[1026], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3936], x=[1092, 3], y=[32], batch=[1092], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3300], x=[828, 3], y=[32], batch=[828], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3298], x=[903, 3], y=[32], batch=[903], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3918], x=[1032, 3], y=[32], batch=[1032], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 4074], x=[1057, 3], y=[32], batch=[1057], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 4482], x=[1204, 3], y=[32], batch=[1204], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 4526], x=[1176, 3], y=[32], batch=[1176], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3800], x=[1009, 3], y=[32], batch=[1009], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3700], x=[957, 3], y=[32], batch=[957], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3818], x=[981, 3], y=[32], batch=[981], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 4256], x=[1088, 3], y=[32], batch=[1088], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 4070], x=[1080, 3], y=[32], batch=[1080], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 4336], x=[1150, 3], y=[32], batch=[1150], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 4134], x=[1083, 3], y=[32], batch=[1083], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3920], x=[983, 3], y=[32], batch=[983], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3892], x=[1014, 3], y=[32], batch=[1014], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3984], x=[1039, 3], y=[32], batch=[1039], ptr=[33])
一批数据量： 32
一批数据： DataBatch(edge_index=[2, 3120], x=[878, 3], y=[24], batch=[878], ptr=[25])
一批数据量： 24

Process finished with exit code 0

以第一批数据的输出 一批数据： Batch(batch=[1145], edge_index=[2, 4284], x=[1145, 3], y=[32]) 为例，batch=[1145] 表示此批数据的节点数有 1145，边数有 4284/2 = 2142。另外，由于数据量不一定能被 batch_size 整除，所以最后一批数据有可能小于 batch_size。

接下来以 ShapeNet 中的 Airplane 数据集（3D 点云数据：指在一个三维坐标系统中的一组向量的集合）为例进行说明，首先需要加载数据集。

加载数据集,并未经过转换的原始数据如下：

from torch_geometric.datasets import ShapeNet
dataset = ShapeNet(root='Airplane', categories=['Airplane'])
print(dataset[0])

 结果：

Processing...
Done!
Data(x=[2518, 3], y=[2518], pos=[2518, 3], category=[1])

Process finished with exit code 0

 可通过变换从点云生成最近邻图，将点云数据集转换为图数据集：

import torch_geometric.transforms as T
dataset = ShapeNet(root='Airplane', categories=['Airplane'],
                    pre_transform=T.KNNGraph(k=6)) # 进行 KNN 聚类操作

 结果：

Data(x=[2518, 3], y=[2518], pos=[2518, 3], category=[1])

Process finished with exit code 0

当然，仅仅打印 dataset[0] 无法可视化两者的差别。因此很多时候，图数据需要配合专门的函数进行可视化操作。 

4.图数据的可视化

相对于其它类型的数据，比如文本、图像等，图数据能够通过可视化给人直观的视觉感受。比如，单纯地通过模型处理前后的图数据的聚合效果可以判断模型的基本性能。接下来通过一个简单地案例实现对图数据的可视化。

首先定义可视化函数：

import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline

def visualize_networkx(graph, color):
    plt.figure(figsize=(8,8)) # 设定图画区域大小
    nx.draw_networkx(graph, with_labels=False,node_color=color) # 画图
    plt.show()

    在进行可视化之前，首先需要对图数据进行格式转化，转化为 networkx：

• 假如 to_undirected=True：应用 to_networkx 将 torch_geometric.data.Data 转化为 networkx.DiGraph 。
• 假如 to_undirected=False：应用 to_networkx 将 torch_geometric.data.Data 转化为 networkx.Graph 。

from torch_geometric.datasets import KarateClub
from torch_geometric.utils import to_networkx

dataset = KarateClub()[0] # 取图数据集
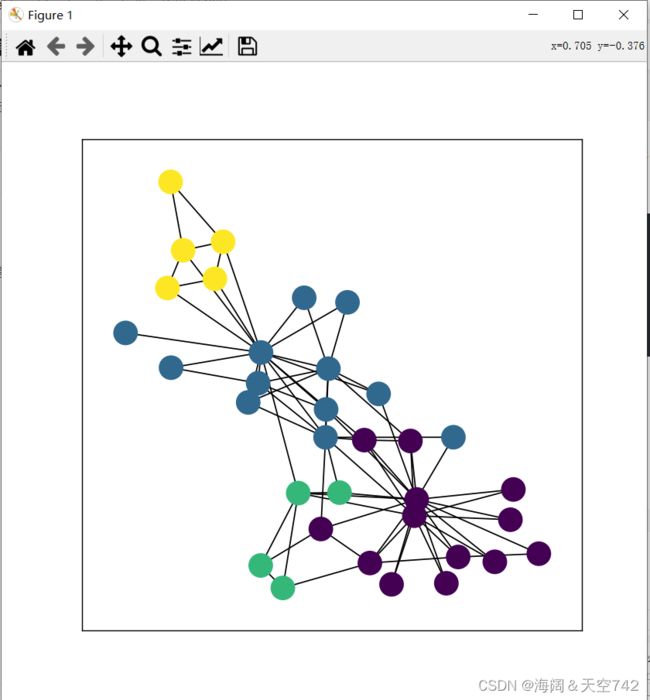
G = to_networkx(dataset,to_undirected=True) # 转化为 networkx
visualize_networkx(G, color=dataset.y) # 画图

在上图中，相同颜色的点为同一类别，可直观了解数据的分布特性。 

5.实验总结

   在以上的实验中，我们对 PyG 中的图数据类以及自身具备的图数据进行了实践，整体而言比较简单，和 PyTorch 中的一些相关操作也有相似之处。唯一美中不足的是，在加载 PyG 中的图数据时经常会遇到问题，需要手工下载数据集并且修改原代码。