【补题笔记】AtCoder Beginner Contest 256 A~Ex
A - 2^N
题目链接
直接输出 1 1 1左移 N N N位即可。
#includeB - Batters
题目链接
直接按照题目给定的流程模拟即可。移动纸片的时候需要从右往左移,防止前面的先移动,把后面的纸片覆盖掉了。
#includeC - Filling 3x3 array
题目链接
数据范围很小,所以可以大胆暴力。暴力枚举左上角四个数即可,然后check剩下的 5 5 5个数是否可以符合要求,可以符合则计数器+1。
#includeD - Union of Interval
题目链接
将所有区间按照左端点从小到大→右端点从小到大的顺序排序。从头到尾扫一遍区间,记录一个当前适用的左端点的值 x x x,每遇到一个区间,如果他的左端点在以 x x x为左端点的大区间内,则根据当前区间的右端点更新这个大区间的右端点;如果这个区间的左端点不在大区间内,则以这个区间的左端点为新的 x x x,开辟一个新的大区间。
#includeE - Takahashi’s Anguish
题目链接
将每一个人视作图上的一个点,第 i i i个人就是第 i i i号结点,对于每一个 i i i,从第 i i i号结点向第 X i X_i Xi号结点连一条边权为 C i C_i Ci的有向边。最后连成的图如果有环,说明环上的所有人不可能有一种方案不产生不愉快的值。如果这个人不在环上,则可以通过调换位置不产生不愉快的值。
我们发现这个环上的所有点都只会出现在一个环中,不会有一个点同时出现在两个环中。因为每一个点只有一个出度,如果这个点同时出现在两个环,作为两个环的交集的点中至少有一个点要有至少为 2 2 2的出度。
身在环上的人,我们可以通过调换顺序的方式,让只有一个人产生不愉快的值。也就是说这个题的答案就是所有的环的最小边权的和。
#includeF - Cumulative Cumulative Cumulative Sum
题目链接
可以轻松推出: D x = ∑ i = 1 x ( x − i + 1 ) ( x − i + 2 ) 2 A i D_x=\displaystyle\sum\limits_{i=1}^x \frac{(x-i+1)(x-i+2)}{2}A_i Dx=i=1∑x2(x−i+1)(x−i+2)Ai。
对这个式子进行一个简单的拆项,然后我们发现里面有 A i A_i Ai项、 i A i iA_i iAi项和 i 2 A i i^2A_i i2Ai项。根据这几项对式子进行一个简单的处理,得到:
D x = 1 2 ( ∑ i = 1 x i 2 A i − ( 2 x + 3 ) ∑ i = 1 x i A i + ( x + 1 ) ( x + 2 ) 2 ∑ i = 1 x A i ) D_x=\frac{1}{2}(\displaystyle\sum\limits_{i=1}^x i^2A_i-(2x+3)\displaystyle\sum\limits_{i=1}^x iA_i +\frac{(x+1)(x+2)}{2}\displaystyle\sum\limits_{i=1}^x A_i) Dx=21(i=1∑xi2Ai−(2x+3)i=1∑xiAi+2(x+1)(x+2)i=1∑xAi)
我们用线段树/树状数组分别维护 A i A_i Ai、 i A i iA_i iAi、 i 2 A i i^2A_i i2Ai,对于每一次询问,分别求三个前缀和,然后根据上式进行求值即可。(取模有点小烦)
#includeG - Black and White Stones
题目链接
我们发现边的长度很小,也就是说我们每一条边可以选择的相同石子数量的可能取值并不多。那么我们可以考虑将问题拆解成:对于所有的 i ( 0 ≤ i ≤ D + 1 ) i(0\leq i\leq D+1) i(0≤i≤D+1),每一条边都有 i i i个黑色石头有多少种放法。最后的答案就是这 D + 2 D+2 D+2个问题的答案的和。
现在求解这样的子问题:每一条边都有 k k k个黑色石头有多少种放法。对于这道题目而言,边与边的交界点是非常特殊的点,因为如果这个点是黑色石头,那么这个黑色石头会对两条边都产生贡献。题目中本质上是一个 N N N条边的环,但是除了边与边的交界处以外,剩下的点之间怎么选取,彼此之间是完全没有联系的,所以我们要限制的只有交界处的点。
考虑随便选取一个两边交界处,将这个环拆成一条直链。对于这条直链的限制条件就是:首尾的颜色必须相同。
然后对于每一条边的点,由于交界处会对两条边都产生贡献,所以我们就以交界处的情况作为状态。对于每一条边,我们有以下四种情况:
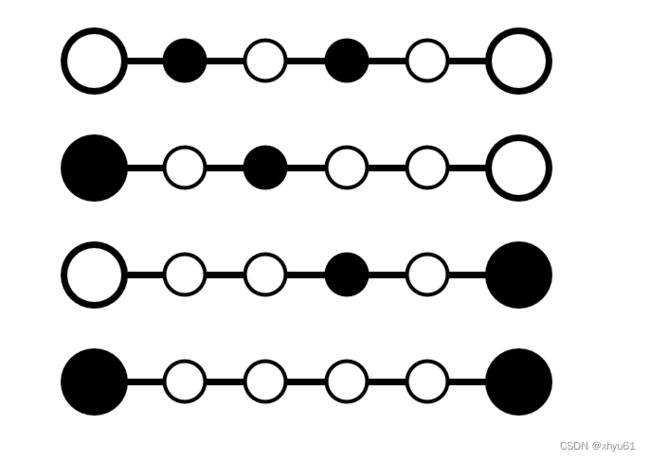
当每条边只能有两个黑色石头的时候,情况如上。我们假设从左向右是我们放石头的顺序,同时也是访问边的顺序,那么通过图可以看出,大圆是边与边的交界处,其颜色会影响两条边;小圆在边的中间,其黑色石子的数量与两边的大圆有关,但是内部这些小圆顺序的调换与否不会对其他边产生任何影响。
我们设上一条边处理完后,末尾是白色的方案数是 x x x,末尾是黑色的方案数是 y y y,这一条边处理完后末尾是白色的方案数是 X X X,末尾是黑色的方案数是 Y Y Y。于是有:
X = x × ( D − 2 k ) + y × ( D − 2 k − 1 ) X=x\times \binom{D-2}{k} + y\times \binom{D-2}{k-1} X=x×(kD−2)+y×(k−1D−2)
Y = x × ( D − 2 k − 1 ) + y × ( D − 2 k − 2 ) Y=x\times \binom{D-2}{k-1} + y\times \binom{D-2}{k-2} Y=x×(k−1D−2)+y×(k−2D−2)
可以看出,这一条边的方案数可以通过上一条边的结果来推出,也就是构成了一个递推式。也就是说,我们只需要将初始值设置好,然后每一条边递推一次就可以得出这个问题的结果。但是,边数是 1 0 12 10^{12} 1012的范围,如果真的按边递归,一定会超时。
我们发现,每一次从上一个边的方案数推出这条边的方案数时,所乘的系数都没有变。这样的话,就可以用矩阵快速幂解决这个问题:我们试着将上面两个公式进行一个变型,变成矩阵的形式:
[ X e Y e ] = [ x 0 y 0 ] [ ( D − 2 k ) ( D − 2 k − 1 ) ( D − 2 k − 1 ) ( D − 2 k − 2 ) ] n \left[ \begin{matrix} X_e & Y_e \end{matrix} \right] = \left[ \begin{matrix} x_0 & y_0 \end{matrix} \right] \left[ \begin{matrix} \binom{D-2}{k} & \binom{D-2}{k-1} \\ \binom{D-2}{k-1} & \binom{D-2}{k-2} \end{matrix} \right]^n [XeYe]=[x0y0][(kD−2)(k−1D−2)(k−1D−2)(k−2D−2)]n
其中 X e , Y e X_e,Y_e Xe,Ye表示这 n n n条边走完之后以白色石头结尾、以黑色石头结尾分别的方案数, x 0 , y 0 x_0,y_0 x0,y0是整个过程开始前的最初状态(一会儿进行讨论)。
要注意的是,在计算组合数时,对于 ( n m ) \binom{n}{m} (mn),我们可能会出现 n < m n
这样的话,由于矩阵很小,可以作为一个常数,然后我们就从 O ( n ) O(n) O(n)变成了 O ( log n ) O(\log n) O(logn)。
我们设以白色石头作为链的最开始,经过 n n n条边后以白色石头作为结尾的方案数为 W W W,以黑色石头作为链的最开始,经过 n n n条边后以黑色石头作为结尾的方案数为 B B B。
这个子问题的最终答案就是 W + B W+B W+B。
也就是说,我们要求的就是这两种链的情况。
- 令 x 0 = 1 , y 0 = 0 x_0=1,y_0=0 x0=1,y0=0,进行矩阵快速幂运算后, W = X e W=X_e W=Xe。
- 令 x 0 = 0 , y 0 = 1 x_0=0,y_0=1 x0=0,y0=1,进行矩阵快速幂运算后, B = Y e B=Y_e B=Ye。
将所有的子问题答案算完之后进行累加并取模,就得到了最终的结果。
#includeEx - I like Query Problem
题目链接
势能线段树的模板题。吉老师的线段树论文
考虑到操作只有对区间每个数做除法,以及区间赋值。所以我们为了精简写法,将除法操作用赋值的方式来实现。
我们对线段树的每一个节点维护区间和、赋值标记、最大值、最小值。在进行除法的时候,判断最大值与最小值分别除以 x x x,看看两者结果是否相同,如果相同,则说明这个区间内的所有数值在除以 x x x后的结果都是相同的,那么就对这个区间进行区间赋值。否则,递归往孩子结点去寻找。其他的和普通线段树是一样的操作。
#include