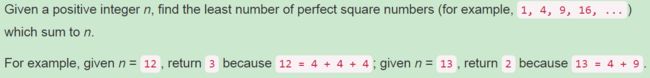leetcode解题笔记--part1--dynamic programming

 

 

---

 5. Longest Palindromic Substring  ❤

 62. Unique Paths

 63. Unique Paths II  ❤

 64. Minimum Path Sum

 91. Decode Ways

 95. Unique Binary Search Trees II  ❤❤

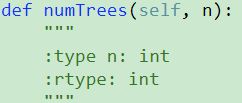
 96. Unique Binary Search Trees    ❤❤

 120. Triangle

 139. Word Break   ❤❤

 152. Maximum Product Subarray  ❤❤

 213. House Robber II

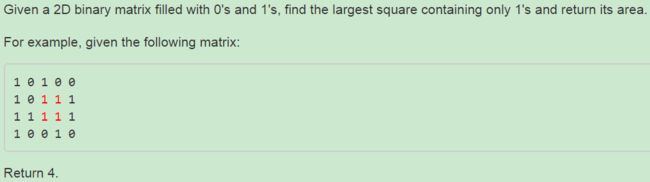
 221. Maximal Square  ❤

 264. Ugly Number II    ❤❤

 279. Perfect Squares    ❤❤

 300. Longest Increasing Subsequence  ❤

 304. Range Sum Query 2D - Immutable  

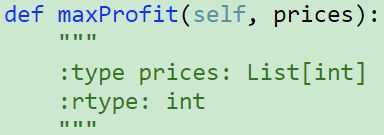
 309. Best Time to Buy and Sell Stock with Cooldown  ❤❤

 322. Coin Change  ❤

 338. Counting Bits   ❤

 343. Integer Break  ❤❤

 351. Android Unlock Patterns   ❤❤

 357. Count Numbers with Unique Digits  ❤

 361. Bomb Enemy   ❤

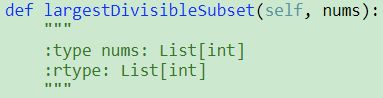
 368. Largest Divisible Subset ❤

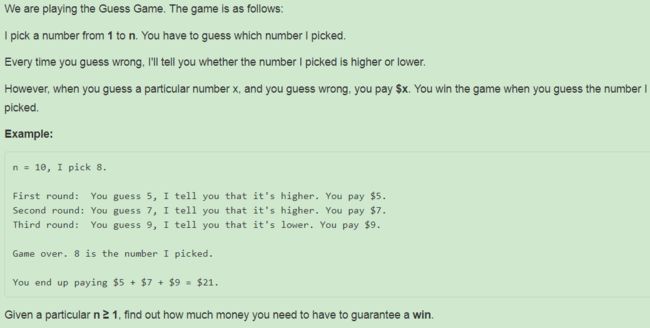
 375. Guess Number Higher or Lower II  ❤❤

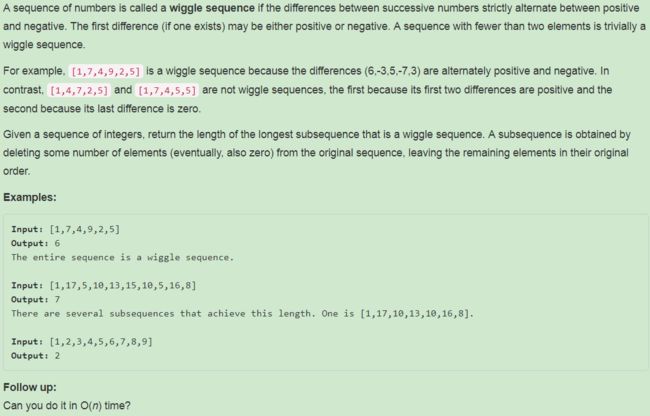
 376. Wiggle Subsequence

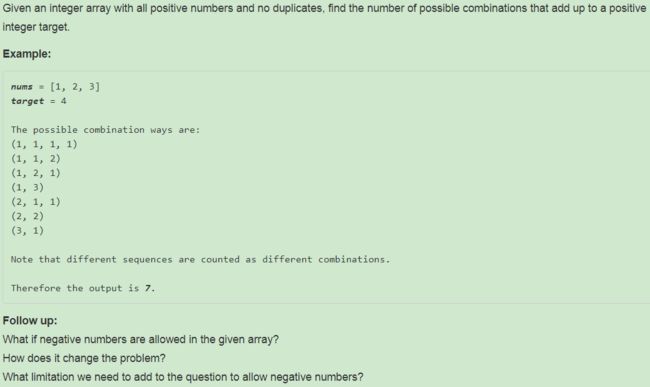
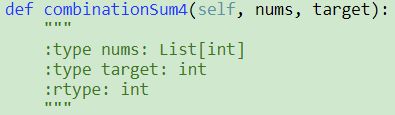
 377. Combination Sum IV

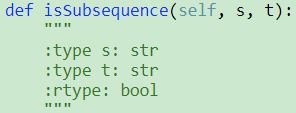
 392. Is Subsequence

 413. Arithmetic Slices

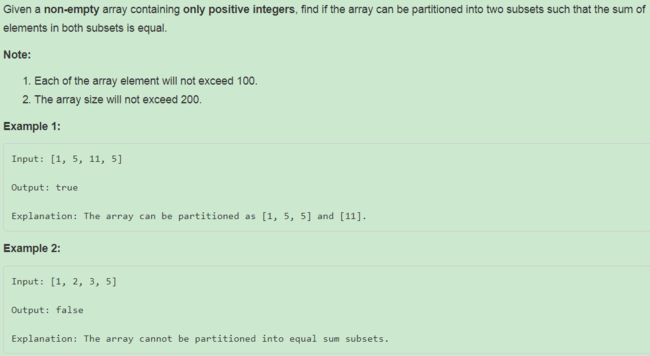
 416. Partition Equal Subset Sum   ❤❤

 418. Sentence Screen Fitting   ❤❤

 464. Can I Win  ❤❤

 467. Unique Substrings in Wraparound String  ❤

 474. Ones and Zeroes   ❤❤

 486. Predict the Winner  ❤❤

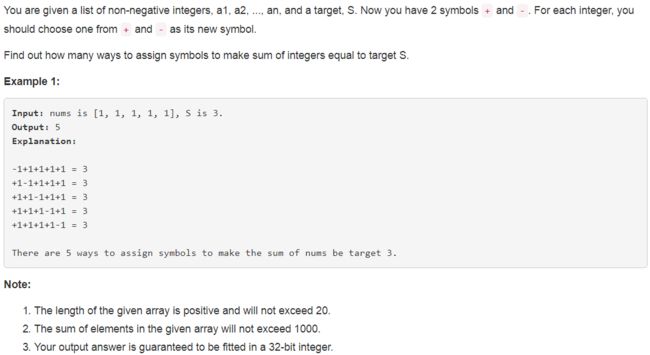
 494. Target Sum  ❤

 516. Longest Palindromic Subsequence 

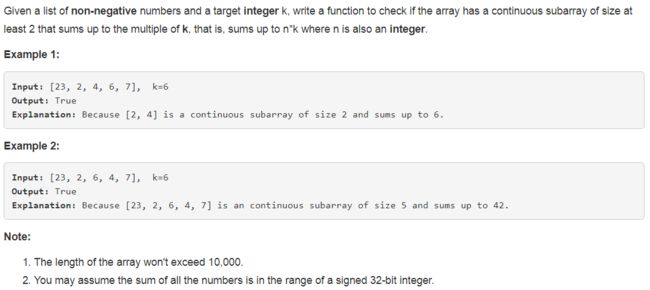
 523. Continuous Subarray Sum ❤❤

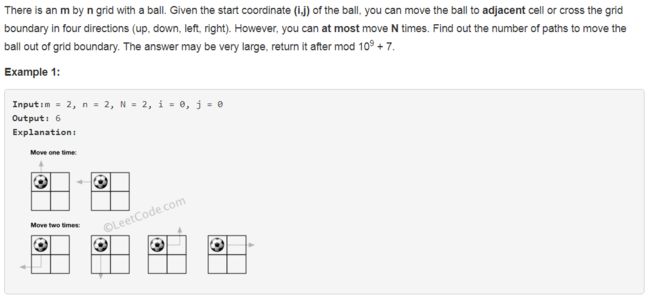
 576. Out of Boundary Paths  ❤

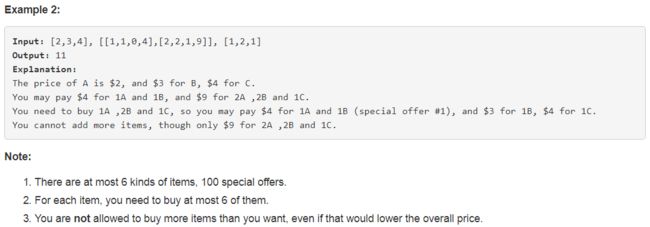
 638. Shopping Offers  ❤❤

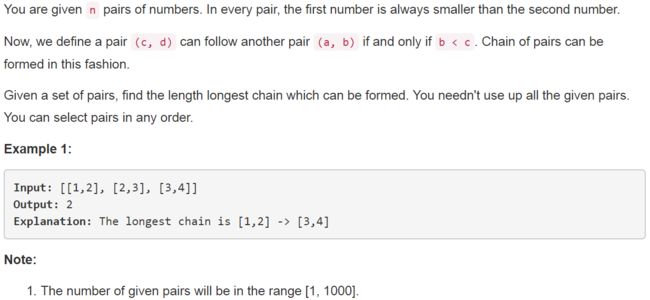
 646. Maximum Length of Pair Chain

 647. Palindromic Substrings

 650. 2 Keys Keyboard  ❤❤

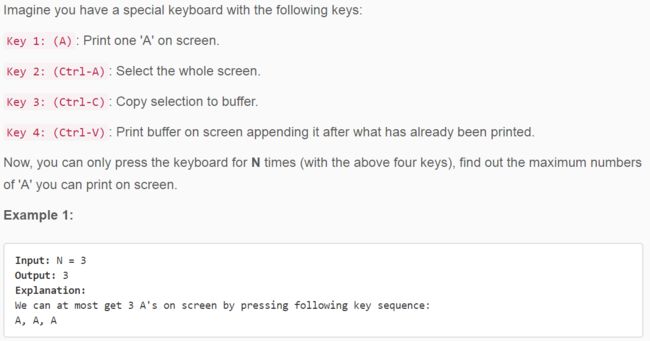
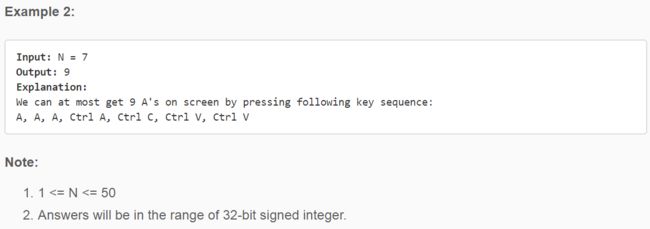
 651. 4 Keys Keyboard  ❤❤

 673. Number of Longest Increasing Subsequence

 688. Knight Probability in Chessboard

 698. Partition to K Equal Sum Subsets

 712. Minimum ASCII Delete Sum for Two Strings

 714. Best Time to Buy and Sell Stock with Transaction Fee ❤❤

 718. Maximum Length of Repeated Subarray

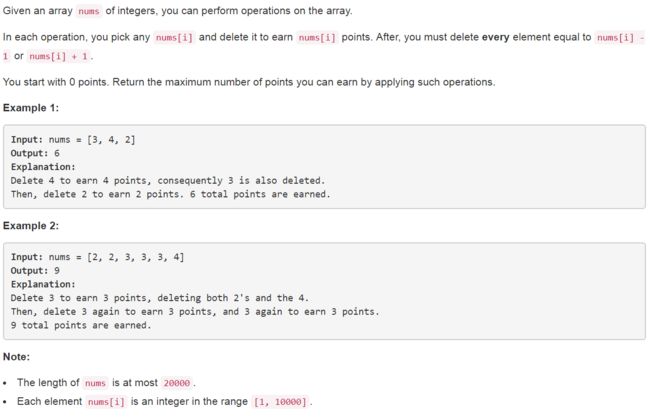
 740. Delete and Earn

---

 

 

 

 

 

 

 

---

5. Longest Palindromic Substring 【Medium】  返回目录

---

 题目：

解体思路：

dp[i][j] = dp[i+1][j-1] & s[i+1]==s[j-1]

时间复杂度O(n^2)

code:  AC  但是时间很长

 1 def longestPalindrome(self, s):
 2         """
 3         :type s: str
 4         :rtype: str
 5         """
 6         if not s:
 7             return ""
 8         length = len(s)
 9         max_length = 1
10         result = s[0]
11         dp = [[0 for j in range(length)] for i in range(length)]
12         for i in range(length):
13             dp[i][i] = 1
14             if i > 0:
15                 dp[i][i-1] = 1
16         for i in range(length-2,-1,-1):
17             for j in range(i+1,length):
18                 if dp[i+1][j-1] and s[i]==s[j]:
19                     dp[i][j] = 1
20                     if j-i+1 > max_length:
21                         max_length = j-i+1
22                         result = s[i:j+1]
23         return result

看来下答案，有个线性时间的算法，Manacher马拉车算法，就是专门解决找字符串中最长回文子串

https://www.cnblogs.com/grandyang/p/4475985.html

code:

 1 def longestPalindrome(self, s):
 2         """
 3         :type s: str
 4         :rtype: str
 5         """
 6         T = '#'.join('^{}$'.format(s))
 7         n = len(T)
 8         p = [1] * n
 9         mx = 0
10         center = 0
11         for i in range(1,n-1):
12             p[i] = min(p[2*center-i], mx-i) if mx > i else 1
13             while T[i+p[i]] == T[i-p[i]]:
14                 p[i] += 1
15             if i + p[i] > mx:
16                 center,mx = i, i+p[i]
17         maxLen, centerIndex = max((n,i) for i,n in enumerate(p))
18         return s[(centerIndex-maxLen)//2:(centerIndex+maxLen)//2-1]

 

 

 

 

 

 

 

 

 

---

91. Decode Ways 【Medium】  返回目录

---

题目：

 解题思路：

先写出编码当前位置时，与之前结果的递推关系，再考虑各种情况，具体思路见代码

 1 def numDecodings(self, s):
 2         """
 3         :type s: str
 4         :rtype: int
 5         """
 6         if not s or s[0]=='0':
 7             return 0
 8         res1_cur, res1_pre, res1_prepre = 1,1,1
 9         res2_cur, res2_pre, res2_prepre = 0,0,0
10         for i in range(1,len(s)):
11             if s[i]=='0':
12                 res1_cur = 0
13                 if 10<=int(s[i-1:i+1])<=26:
14                     res2_cur = res1_prepre+res2_prepre
15                 else:
16                     return 0
17             else:
18                 res1_cur = res1_pre+res2_pre
19                 if 10<=int(s[i-1:i+1])<=26:
20                     res2_cur = res1_prepre+res2_prepre
21                 else:
22                     res2_cur = 0
23             res1_pre,res1_prepre = res1_cur,res1_pre
24             res2_pre,res2_prepre = res2_cur,res2_pre
25         return res1_cur+res2_cur

 

 

 

 

 

---

95. Unique Binary Search Trees II 【Medium】  返回目录

---

 题目：

 解题思路：

注意这题是二叉树，所以节点左边的树节点都小于根节点，节点右边的树节点都大于根节点

 参考的别人的答案，用的迭代方法：

 1 # Definition for a binary tree node.
 2 # class TreeNode(object):
 3 #     def __init__(self, x):
 4 #         self.val = x
 5 #         self.left = None
 6 #         self.right = None
 7 
 8 class Solution(object):
 9     def generate(self,start,end):
10         trees = []
11         for root in range(start,end+1):
12             for left in self.generate(start,root-1):
13                 for right in self.generate(root+1,end):  
14                     node = TreeNode(root)
15                     node.left = left
16                     node.right = right
17                     trees.append(node)
18         return trees or [None]
19     def generateTrees(self, n):
20         """
21         :type n: int
22         :rtype: List[TreeNode]
23         """
24         if n<1:
25             return []
26         return self.generate(1,n)
27         

迭代方法相较于动态规划来说，更加耗时耗空间，因为会重复很多冗余的步骤

但是这道题写动态规划的话会有点繁琐

 

 

 

 

---

96. Unique Binary Search Trees 【Medium】    返回目录

---

 题目：

解题思路:   同上题，而且比上题简单很多

见代码： 使用迭代超时了

 1 def generate(self,start,end):
 2         if start==end+1:
 3             return 1
 4         res = 0
 5         for root in range(start,end+1):
 6             res += self.generate(start,root-1) * self.generate(root+1,end)
 7         return res
 8     def numTrees(self, n):
 9         """
10         :type n: int
11         :rtype: int
12         """
13         return self.generate(1,n)
14         
15         

改成动态规划做法：

code:

 1 class Solution(object):
 2     def numTrees(self, n):
 3         """
 4         :type n: int
 5         :rtype: int
 6         """
 7         res = [[1 for i in range(n+2)] for j in range(n+2)]
 8         for k in range(2,n+1):
 9             for i in range(1,n-k+2):
10                 j = i + k-1
11                 res[i][j] = 0
12                 for m in range(j-i+1):
13                     res[i][j] += res[i][i-1+m] * res[m+i+1][j]                
14         return res[1][n]

看了下参考答案，发现我的要复杂好多，我想要填充一个二维数组，而且还挺恶心的，斜对角线填充，大神的答案只需要填充一个一维数组就可以了

G(n) 表示 (1,n)的二叉树个数     F(i,n)表示以i为根结点range为(1,n)的二叉树个数

这里不用管不同的数字，只要结点数确定的不同二叉树的组成方法就行

 1 def numTrees(self, n):
 2         """
 3         :type n: int
 4         :rtype: int
 5         """
 6         res = [1 if i<2 else 0 for i in range(n+1) ]
 7         for i in range(2,n+1):
 8             for j in range(i):
 9                 res[i] += res[j] * res[i-j-1]
10         return res[n]

 

 

 

 

 

 

---

139. Word Break 【Medium】  返回目录

---

 题目：

 解题思路：

这道题我没什么思路，就直接看了答案，直接看代码吧

 1 def wordBreak(self, s, wordDict):
 2         """
 3         :type s: str
 4         :type wordDict: List[str]
 5         :rtype: bool
 6         """
 7         dp = [0 if i>0 else 1 for i in range(len(s)+1)]
 8         for i in range(len(s)+1):
 9             for j in range(i):
10                 if s[j:i] in wordDict and dp[j]:
11                     dp[i] = 1
12         return dp[len(s)]==1       

这样的题就是要看怎么划分步骤，一步一步的确定当前位置是否正确，模拟人的一个策略从而找出动态规划方程

 

 

 

 

---

213. House Robber II 【Medium】  返回目录

---

 题目：

 先做非环形的情况，dp[i] = max(dp[i-1],dp[i-2]+nums[i])     max(不偷当前，偷当前)

 1 def rob(self, nums):
 2         """
 3         :type nums: List[int]
 4         :rtype: int
 5         """
 6         n = len(nums)
 7         if n<2: return sum(nums)
 8         dp = [nums[0] if i<1 else 0 for i in range(n)]
 9         dp[1] = max(nums[0],nums[1])
10         for i in range(2,n):
11             dp[i] = max(dp[i-1],dp[i-2]+nums[i])
12         return dp[n-1]

 

这种情况是可以节省空间的 O(n)-> O(1)

 1 def rob(self, nums):
 2         """
 3         :type nums: List[int]
 4         :rtype: int
 5         """
 6         n = len(nums)
 7         if n<2: return sum(nums)
 8         prepre = nums[0]
 9         pre = max(nums[0],nums[1])
10         cur = pre
11         for i in range(2,n):
12             cur = max(pre,prepre+nums[i])
13             pre,prepre = cur,pre
14         return cur

 

对于环形，只需要断开一头就变成了链状，这里假设不偷第i家，那么i-1和i+1都不会有限制关系，所以这里两种情况，不偷连续两家取结果最大值，为了方便计算，这里取0和n-1

1  def circle_rob(self, nums):
2         n = len(nums)
3         if n == 1:
4             return nums[0]
5         return max(rob(nums[0:n-1]),rob(nums[1:n]))

 

 

 

 

 

 

---

221. Maximal Square 【Medium】  返回目录

---

 题目：

解题思路：

if matrix[i][j] = 0:  dp[i][j] = 0

else:  dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1    O(mn) space  O(mn) time

进行优化，只是依赖于前面三个变量，所以只需要一列   O(mn) time  O(min(m,n)) space

O(mn) space 的代码很好实现

 1 def maximalSquare(self, matrix):
 2         """
 3         :type matrix: List[List[str]]
 4         :rtype: int
 5         """
 6         m = len(matrix)
 7         if not m:
 8             return 0
 9         n = len(matrix[0])
10         res = 0
11         dp = [[int(matrix[i][j]) for j in range(n)] for i in range(m)]
12         for l in dp:
13             if sum(l) > 0:
14                 res = 1
15         for i in range(1,m):
16             for j in range(1,n):
17                 if matrix[i][j] == '1': 
18                     dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1
19                     if res < dp[i][j]:
20                         res = dp[i][j]
21         return res**2

 

优化代码，只保留两列

 1 def maximalSquare(self, matrix):
 2         """
 3         :type matrix: List[List[str]]
 4         :rtype: int
 5         """
 6         m = len(matrix)
 7         if not m:
 8             return 0
 9         n = len(matrix[0])
10         pre = [int(matrix[i][0]) for i in range(m)]
11         res = max(pre)
12         cur = [0 for i in range(m)]
13         for j in range(1,n):
14             cur[0] = int(matrix[0][j])
15             res = max(res,cur[0])
16             for i in range(1,m):
17                 if matrix[i][j] == '1':
18                     cur[i] = min(cur[i-1],min(pre[i-1],pre[i])) + 1
19                     res = max(res,cur[i])   
20                 else:
21                     cur[i] = 0
22             cur,pre = pre,cur
23             print(cur,pre)
24         return res**2

 

优化后的代码如下：只保留一列

 1 def maximalSquare(self, matrix):
 2         """
 3         :type matrix: List[List[str]]
 4         :rtype: int
 5         """
 6         m = len(matrix)
 7         if not m:
 8             return 0
 9         n = len(matrix[0])
10         dp = [0 for i in range(m+1)]
11         res = 0
12         pre = 0
13         
14         for j in range(n):
15             for i in range(1,m+1):
16                 temp = dp[i]     #保存之前的dp[i]的结果
17                 if matrix[i-1][j] == '1':
18                     dp[i] = min(dp[i],min(dp[i-1],pre)) + 1    dp[i]就是pre[i],  dp[i-1]已经是新计算过的也就是cur[i-1]
19                     res = max(res,dp[i])
20                 else:
21                     dp[i] = 0
22                 pre = temp      #pre[i-1]
23         return res**2

 

 

 

 

---

264. Ugly Number II 【Medium】    返回目录

---

 题目：

解题思路：

1， 2， 3，   4， 5，   6，      8，     9，   10， 12

1， 2， 3， 2x2,  5， 2x3， 4x2， 3x3， 2x5， 6x2 

有点难，直接看答案了

k[1] = min(k[0]x2, k[0]x3, k[0]x5)   取的是k[0]x2,所以我们把2的指针移向k[0]->k[1]

k[2] = min(k[1]x2, k[0]x3, k[0]x5)   对于6这种情况，要同时移动指针2和指针3

 1 def nthUglyNumber(self, n):
 2         """
 3         :type n: int
 4         :rtype: int
 5         """
 6         if n<0: return False
 7         if n == 1:
 8             return 1
 9         t2 = t3 = t5 = 0
10         dp = [1 if i<1 else 0 for i in range(n)]
11         for i in range(1,n):
12             dp[i] = min(dp[t2]*2, min(dp[t3]*3, dp[t5]*5))
13             if dp[i] == dp[t2]*2: t2 += 1
14             if dp[i] == dp[t3]*3: t3 += 1
15             if dp[i] == dp[t5]*5: t5 += 1
16         return dp[n-1]
17         

 

 

 

 

 

---

279. Perfect Squares 【Medium】  返回目录

---

题目：

for i in range(n):

dp[n] = min(dp[n], dp[i]+dp[n-i])

边界条件：

dp[0] = 0

dp[1] = 1

这个算法超时了 ：  O(n^2)

 1 def numSquares(self, n):
 2         """
 3         :type n: int
 4         :rtype: int
 5         """
 6         dp = [1 if i==1 else 0 for i in range(n+1)]
 7         for i in range(2,n+1):
 8             res = i**0.5
 9             if res.is_integer():
10                     dp[i] = 1
11             else:
12                 for k in range(1,i//2+1):
13                     if not dp[i]:
14                         dp[i] = dp[k]+dp[i-k]
15                     else:
16                         dp[i] = min(dp[i],dp[k]+dp[i-k])
17         return dp[n]

 

 知道我败在了哪里吗？败在第二个循环上，直接+1循环真的很笨啊，具体见代码：

(For each i, it must be the sum of some number (i-j*j)) and a perfect square number j*j)

还是超时了，python有毒

 1 import sys
 2 class Solution:
 3     def numSquares(self, n):
 4         """
 5         :type n: int
 6         :rtype: int
 7         """
 8         dp = [sys.maxsize for i in range(n+1)]
 9         dp[0] = 0
10         for i in range(1,n+1):
11             j = 1
12             while j*j <= i:
13                 dp[i] = min(dp[i],dp[i-j*j]+1)
14                 j += 1
15         return dp[n]

 看了一个答案，唯一的可以pass不超时的python代码：

 1 class Solution:
 2     _dp = [0]    类的公共属性，建立不同的对象的时候可以进行复用，这是针对测试样例是从1递增的，所以在计算567的时候可以复用566的答案
 3     def numSquares(self, n):
 4         """
 5         :type n: int
 6         :rtype: int
 7         """
 8         dp = self._dp
 9         while len(dp) <= n:
10             dp += min(dp[-i*i] for i in range(1,int(len(dp)**0.5+1))) + 1,
11         return dp[n]

 

 

 

 

 

 

---

300. Longest Increasing Subsequence 【Medium】   返回目录

---

 题目：

for j in range(i):    if nums[j]

O(n^2)

 1 def lengthOfLIS(self, nums):
 2         """
 3         :type nums: List[int]
 4         :rtype: int
 5         """
 6         n = len(nums)
 7         if not n: return 0
 8         dp = [1 for i in range(n)]
 9         for i in range(1,n):
10             for j in range(i):
11                 if nums[j] < nums[i]:
12                     dp[i] = max(dp[i],dp[j]+1)
13         return max(dp)

 

 O(nlogn)

 1 def lengthOfLIS(self, nums):
 2         """
 3         :type nums: List[int]
 4         :rtype: int
 5         """
 6         tails = [0] * len(nums)
 7         size = 0
 8         for x in nums:
 9             i, j = 0, size
10             while i != j:
11                 m = (i + j) // 2
12                 if tails[m] < x:
13                     i = m + 1
14                 else:
15                     j = m
16             tails[i] = x
17             size = max(i + 1, size)
18         return size

 

tail[i]记录的是长度为i+1的上升子序列的最小尾部    size是当前的最大长度  因为tail可能是升序的，所以可以使用二分查找进行更新

 

 

 

 

 

---

304. Range Sum Query 2D - Immutable 【Medium】     返回目录

---

 题目：

说是对象初始化一次，但是会连续call很多次sumRegion,所以我们不能直接循环做加法，会超时，所以要事先算好总和，用对角点做减法

 1 class NumMatrix:
 2     def __init__(self, matrix):
 3         """
 4         :type matrix: List[List[int]]
 5         """
 6         if matrix is None or not matrix:
 7             return 
 8         n,m = len(matrix),len(matrix[0])
 9         self.sums = [[0 for j in range(m+1)] for i in range(n+1)]
10         for i in range(1,n+1):
11             for j in range(1,m+1):
12                 self.sums[i][j] = matrix[i-1][j-1] + self.sums[i][j-1] + self.sums[i-1][j] - self.sums[i-1][j-1]
13 
14     def sumRegion(self, row1, col1, row2, col2):
15         """
16         :type row1: int
17         :type col1: int
18         :type row2: int
19         :type col2: int
20         :rtype: int
21         """
22         row1, col1, row2, col2 = row1+1, col1+1, row2+1,col2+1
23         return self.sums[row2][col2] - self.sums[row2][col1-1] - self.sums[row1-1][col2] + self.sums[row1-1][col1-1]
24 
25 
26 # Your NumMatrix object will be instantiated and called as such:
27 # obj = NumMatrix(matrix)
28 # param_1 = obj.sumRegion(row1,col1,row2,col2)

 

 

 

 

 

 

---

309. Best Time to Buy and Sell Stock with Cooldown 【Medium】   返回目录

---

 题目：

解题思路：

动态规划主要是要能找到相应的状态，以及状态之间的转移方程，有点类似于状态机

这里主要有三个状态，如下图(复制的别人的解法)

s0: rest[i] = max(sell[i-1], buy[i-1], rest[i-1])    为了表示buy[i]<=rest[i]，还加上了sell[i-1]，所以不会出现[buy, rest, buy]的情况  毫无意义，可以删除，因为rest[i]=sell[i-1]

s1:  buy[i] = max(rest[i-1]-price, buy[i-1])

s2: sell[i] = max(buy[i-1]+price, sell[i-1])

又因为 rest[i] = sell[i-1]

进行替换变成：

buy[i] = max(sell[i-2]-price, buy[i-1])

sell[i] = max(buy[i-1]+price, sell[i-1])

继续优化，把O(n)space 改成 O(1) space

 1 def maxProfit(self, prices):
 2         """
 3         :type prices: List[int]
 4         :rtype: int
 5         """
 6         if len(prices) < 2:
 7             return 0
 8         sell, buy, prev_sell, prev_buy = 0, -prices[0], 0, 0
 9         for price in prices:
10             prev_buy = buy
11             buy = max(prev_sell - price, prev_buy)
12             prev_sell = sell
13             sell = max(prev_buy + price, prev_sell)
14         return sell

 

 

 

 

 

 

---

322. Coin Change 【Medium】   返回目录

---

 题目：

 不是特别难，

for i in range(amount):

　　for j in coins:

　　　　dp[i] = min(dp[i], 1+dp[i-j])

代码如下： 超时了  过了样例 172/182

 1 def coinChange(self, coins, amount):
 2         """
 3         :type coins: List[int]
 4         :type amount: int
 5         :rtype: int
 6         """
 7         if not amount:
 8             return 0
 9         dp = [1 if i+1 in coins else -1 for i in range(amount)]
10         for i in range(amount):
11             if dp[i]!=1:
12                 for j in coins:
13                     if j<=i+1 and dp[i-j]!=-1:
14                         if dp[i]==-1:
15                             dp[i] = 1 + dp[i-j]
16                         else:
17                             dp[i] = min(dp[i], 1+dp[i-j])
18         return dp[amount-1]

 

 看了下答案，感觉和我的算法很像啊

def coinChange(self, coins, amount):
        """
        :type coins: List[int]
        :type amount: int
        :rtype: int
        """
        dp = [amount+1 for i in range(amount+1)]
        dp[0] = 0
        for i in range(amount+1):
            for j in coins:
                if j <= i:
                    dp[i] = min(dp[i], dp[i-j]+1)
        return -1 if dp[amount] > amount else dp[amount]

 

 我真笨，不知道怎么处理这个-1，加了很多判断语句，所以才会超时。  而且把1也一块融合到里面了，代码简洁了很多

  

 

 

 

 

---

338. Counting Bits  【Medium】   返回目录

---

 题目：

 这个题，开始我只能想到说如果是奇数，那么它必然只是比前一个偶数多1， 对于进位的情况想不清楚，然后就直接看答案，是属于位操作

比较巧妙的就是发现每个数与它右移1位的数字只有最后一位不同

dp[i] = dp[i>>1] + (i & 1)   注意i & 1要加括号，因为  +  比 &的优先级更高

1 def countBits(self, num):
2         """
3         :type num: int
4         :rtype: List[int]
5         """
6         dp = [0 for i in range(num+1)]
7         for i in range(1,num+1):
8             dp[i] = dp[i>>1] + (i & 1)
9         return dp

 

 

 

 

---

343. Integer Break 【Medium】    返回目录

---

 题目：

 解题思路：

这道题，挺好想的，和为n  假设分成两个数字，j和i-j那么 dp[i] = max(dp[i], dp[j]*dp[i-j])

初始情况就是dp[1] = 1, 但是发现忘记对数字它本身是否要继续分进行讨论，2如果要继续分的话只能是1*1 但是它本身就是2，  所以改为

dp[i] = max(dp[i], max(j,dp[j])*max(dp[i-j],i-j))     我写代码的时候愚蠢了一下  写成了 dp[i] = max(dp[i],max(dp[j]*dp[i-j],  j*(i-j)))这就是很蠢了

 1 def integerBreak(self, n):
 2         """
 3         :type n: int
 4         :rtype: int
 5         """
 6         dp = [1 if i==1 else 0 for i in range(n+1)]
 7         for i in range(2,n+1):
 8             for j in range(1,i//2+1):
 9                 dp[i] = max(dp[i], max(dp[j],j)*max(dp[i-j],(i-j)))
10         return dp[n]

 

这个解法 O(n^2) time  O(n) space

看参考答案发现有数学的解法  O(n) time  O(1) space

f = x(N-x)  什么时候取最大  中值的时候，所以 当N是偶数时 (N/2)*(N/2)  当N为奇数时   (N-1)/2 * (N+1)/2

当划分后的乘积大于 N本身时，才需要进行划分

(N/2) * (N/2) >= N,  N>= 4

(N-1)/2 * (N+1)/2 >= N ,  N>= 5

以上式子说明 factors必然是 小于4的  因为大于等于4就是可分的， 所以就是 1, 2, 3,   1不用考虑，那就只剩下2和3了，那就尽可能的使用3  因为 3*3 >2*2*2 所以说最优的乘积中最好不要多于3个2

代码如下：

 1 def integerBreak(self, n):
 2         """
 3         :type n: int
 4         :rtype: int
 5         """
 6         if n==2:
 7             return 1
 8         if n==3:
 9             return 2
10         res = 1
11         while n> 4:
12             res *= 3
13             n -= 3
14         res *= n
15         return res

 

 

 

 

 

---

351. Android Unlock Patterns 【Medium】   返回目录   【Locked】

---

 题目：   Google 面试题

 虽然是分在dp标签下的，但是看答案大多是用的dfs+回溯

我们可以发现 1， 3 ，7， 9是对称的，所以只需要以其中一个作为开始点，结果乘以4

2， 4,  6， 8也是对称的， 5单独一个

有个限制条件就是访问两个数字之间的数字必须要访问过，所以用mid数组记录两个数字之间的数字是什么 

dfs(m,n,len,num)  指当前长度为len, 初始访问结点是num, 长度在m,n之间的解锁方式个数

代码如下：

 1 class Solution(object):
 2     def dfs(self, m, n, len, num):
 3         res = 0
 4         if len >= m: 
 5             res += 1
 6         len += 1
 7         if len > n:
 8             return res
 9         visited[num] = True
10         for i in range(1,10):
11             if not visited[i] and visited[mid[num][i]]
12             res += self.dfs(m,n,len,i)
13         visited[num] = False
14         return res
15 
16     def numberOfPatterns(self, m, n):
17         """
18         :type m,n: int
19         :rtype: int
20         """
21         visited = [False for i in range(10)]
22         visited[0] = True
23         mid = [[0 for j in range(10)] for i in range(10)]
24         mid[1][3] = mid[3][1] = 2
25         mid[1][7] = mid[7][1] = 4
26         mid[3][9] = mid[9][3] = 6
27         mid[7][9] = mid[9][7] = 8
28         mid[2][8] = mid[8][2] = mid[4][6] = mid[6][4] = 5
29         mid[1][9] = mid[9][1] = mid[3][7] = mid[7][3] = 5
30         return self.dfs(m,n,1,1)*4 + dfs(m,n,1,2)*4 + dfs(m,n,1,5)

 

我感觉我对dfs的回溯还是不太清楚，好好理清一下，这里主要是算的以num为end的path的个数加和。

 

 

 

 

 

 

 

 

 

---

357. Count Numbers with Unique Digits 【Medium】   返回目录

---

 题目：

 

这就是一个简单的数学问题，要找到n位数中由不同数字组成的数的总个数

dp[1]  0<=x<10   dp[1]=10

dp[2]  第一位数不能是0  所以是 9*9   就是一个全排列问题

dp[3] = 9*9*8

dp[>=11]  = 0

code:  O(1) time   O(1) space

 1 def countNumbersWithUniqueDigits(self, n):
 2         """
 3         :type n: int
 4         :rtype: int
 5         """
 6         if not n:
 7             return 1
 8         count = 10
 9         res = 9
10         remains = 9
11         while n>1 and remains> 0:
12             n -= 1
13             res *= remains
14             count += res
15             remains -= 1
16         return count
17         

 

 

 

 

 

---

361. Bomb Enemy 【Medium】 【Locked】  返回目录

---

 题目：

 感觉locked题目都好难啊，我只想到了最笨的暴力方法，O(m*n)  用空间换时间

用数组记录每个位置的行炸死个数，另一个数组记录每个位置的每列炸死个数,这样O(m+n) space  也就是O(max(m,n)) space  最后再遍历一遍求最大，所以O(m*n) time

进行优化就是对于先遍历行，只需要用一个位置来记录行，所以O(min(m,n)) space, O(m*n) time

 1 def maxKilledEnemies(self, grid):
 2         m = len(grid)
 3         if not m:
 4             return 0
 5         n = len(grid[0])
 6         rowhits = 0 
 7         colhits = [0 for i in range(n)]
 8         res = 0
 9         for i in range(m):
10             for j in range(n):
11                 if not i or grid[i-1][j] == 'W':
12                     colhits[j] = 0
13                     for k in range(i,m): 
14                         if grid[k][j] != 'W':
15                             colhits[j] += grid[k][j] =='E'
16                         else:
17                             break
18                 if not j or grid[i][j-1]=='W':
19                     rowhits = 0
20                     for k in range(j,n):
21                         if grid[i][k]!='W':
22                             rowhits += grid[i][k] == 'E'
23                         else:
24                             break
25                 if grid[i][j] == '0':
26                     res = max(res, colhits[j] + rowhits)
27         return res

 

 

 

 

 

 

 

---

368. Largest Divisible Subset 【Medium】  返回目录

---

 题目：

 

 解题思路：

因为要两两互余，所以如果想要新加入一个新的数字到已确定的集合中，要么这个数字可以被集合中最小的数字除尽，要么就是可以可以除以尽最大的数，要么加大数进去，要么加小数进去，看自己的安排。

用小数更好点，因为可以保持顺序

为了之后能够很好的把结果找出来，所以还需要一个parent数组进行记录

T[i]记录的是nums[i]为构成数组的最小数组的长度

 1 def largestDivisibleSubset(self, nums):
 2         """ 
 3         :rtype: List[int]
 4         """
 5         nums.sort()
 6         n = len(nums)
 7         T = [0 for i in range(n)]
 8         parent = [0 for i in range(n)]
 9         m = 0
10         mi = 0
11         for i in range(n-1,-1,-1):
12             for j in range(i,n):
13                 if nums[j] % nums[i] == 0 and T[i] < 1+T[j]:
14                     T[i] = 1 + T[j]
15                     parent[i] = j
16                     if T[i] > m:
17                         m = T[i]
18                         mi = i
19         res = []
20         for i in range(m):
21             res.append(nums[mi])
22             mi = parent[mi]
23         return res

 

 

 

 

 

 

 

---

375. Guess Number Higher or Lower II 【Medium】  返回目录

---

 题目：

 解题思路：

题目我都不甚理解，只能看答案进行辅助理解了。

for k in [i,j]:  

　　min(k+max(DP(i,k-1),DP(k+1,j)))

0，n中要考虑第一次选择每一个数k的情况，这里综合选取最小的，为自己省钱，然而必须要考虑每次选取的最坏情况也就是之后的max函数

这里就有两种解法，一个递归，一个动规， 动态规划其实就是递归的bottom-up实现，  递归是up-to-bottom

code:  递归   太慢了，才beat 2%

 1 class Solution:
 2     def getMoneyAmount(self, n):
 3         """
 4         :type n: int
 5         :rtype: int
 6         """
 7         table = [[0 for j in range(n+1)] for i in range(n+1)]
 8         return self.dp(table, 1, n)
 9     def dp(self, t, s, e):
10         if s >= e:
11             return 0
12         if t[s][e]!=0:
13             return t[s][e]
14         res = (e-s)*(s+e)//2+1
15         for x in range(s,e+1):
16             tmp = x + max(self.dp(t,s,x-1),self.dp(t,x+1,e))
17             res = min(res,tmp)
18         t[s][e] = res
19         return res
20         

 

动态规划：  beat 50%

 1 def getMoneyAmount(self, n):
 2         """
 3         :type n: int
 4         :rtype: int
 5         """
 6         dp = [[0 for j in range(n+1)] for i in range(n+1)]
 7         for j in range(2,n+1):
 8             for i in range(j-1,0,-1):
 9                 res = j*(j+1)/2
10                 for k in range(i+1,j):
11                     tmp = k + max(dp[i][k-1], dp[k+1][j])
12                     res = min(res, tmp)
13                 dp[i][j] = i if i+1==j else res
14         return dp[1][n]

 

 

 

 

 

 

---

376. Wiggle Subsequence 【Medium】   返回目录

---

 

题目：

解题思路:

居然自己AC了，感动,用了很愚笨的方法  O(n^2) time O(n) space

 1 def wiggleMaxLength(self, nums):
 2         """
 3         :type nums: List[int]
 4         :rtype: int
 5         """
 6         n = len(nums)
 7         if n < 2:
 8             return n
 9         pos = [0 for i in range(n)]
10         neg = [0 for j in range(n)]
11         for i in range(1,n):
12             for j in range(i):    
13                 if nums[i]-nums[j]>0:
14                     pos[i] = max(neg[j] + 1, pos[i])
15                 elif nums[i]-nums[j]<0:
16                     neg[i] = max(pos[j] + 1, neg[i])
17         return max(pos[n-1],neg[n-1])+1
18                 

 

我没想出O(n) 的算法,参考答案：就在我的代码上做了小改进

 1 def wiggleMaxLength(self, nums):
 2         """
 3         :type nums: List[int]
 4         :rtype: int
 5         """
 6         n = len(nums)
 7         if n < 2:
 8             return n
 9         pos = [0 for i in range(n)]
10         neg = [0 for j in range(n)]
11         for i in range(1,n): 
12             if nums[i]-nums[i-1] > 0:
13                 pos[i] = neg[i-1] + 1
14                 neg[i] = neg[i-1]
15             elif nums[i]-nums[i-1]<0:
16                 neg[i] = pos[i-1] + 1
17                 pos[i] = pos[i-1]
18             else:
19                 neg[i] = neg[i-1]
20                 pos[i] = pos[i-1]
21         return max(pos[n-1],neg[n-1])+1
22                 
23         

 

还可以再改进成O(1) space

 1 def wiggleMaxLength(self, nums):
 2         """
 3         :type nums: List[int]
 4         :rtype: int
 5         """
 6         n = len(nums)
 7         if n < 2:
 8             return n
 9         pos = 0
10         neg = 0
11         for i in range(1,n): 
12             if nums[i]-nums[i-1] > 0:
13                 pos = neg + 1
14             elif nums[i]-nums[i-1]<0:
15                 neg = pos + 1
16         return max(pos, neg) + 1
17                 

 

 

 

 

 

 

 

---

377. Combination Sum IV  【Medium】   返回目录

---

 

题目：

 解题思路：

感觉就是一个递归和回溯，很快写完代码，但是TLE

 1 def combinationSum4(self, nums, target):
 2         """
 3         :type nums: List[int]
 4         :type target: int
 5         :rtype: int
 6         """
 7         if target == 0:
 8             return 1
 9         elif target < 0:
10             return 0
11         res = 0
12         for i in nums:
13             res += self.combinationSum4(nums,target-i)
14         return res
15         

所以要看看有没有重复计算的部分，用动态规划记录中间结果

dp[i]记录target为i的方法，然后求dp[target]

居然过了！！ O(target*n)  没有更好的方法了

 1 def combinationSum4(self, nums, target):
 2         """
 3         :type nums: List[int]
 4         :type target: int
 5         :rtype: int
 6         """
 7         dp = [0 for i in range(target+1)]
 8         for i in range(1,target+1):
 9             for num in nums:
10                 if i-num == 0:
11                     dp[i] = dp[i] + 1
12                 elif i-num > 0:
13                     dp[i] = dp[i] + dp[i-num]
14         return dp[target]
15                 

 

 

 

 

 

---

392. Is Subsequence 【Medium】   返回目录

---

 题目：

 

 解题思路：

暴力解法，居然过了嘿嘿   

 1 def isSubsequence(self, s, t):
 2         """
 3         :type s: str
 4         :type t: str
 5         :rtype: bool
 6         """
 7         begin = 0
 8         end = len(t)
 9         match = False
10         for p in s:
11             match = False
12             for i in range(begin,end):
13                 if p == t[i]:
14                     match = True
15                     begin = i+1
16                     break
17             if not match:
18                 return False
19         return True
20         

 

优化成 O(len(t))

 1 def isSubsequence(self, s, t):
 2         """
 3         :type s: str
 4         :type t: str
 5         :rtype: bool
 6         """
 7         i = j = 0
 8         m = len(s)
 9         if not m:
10             return True
11         n = len(t)
12         while j < n:
13             if s[i] == t[j]:
14                 i += 1
15                 if i == m:
16                     return True
17             j += 1
18         return False

 

 

 

 

 

 

---

413. Arithmetic Slices 【Medium】  返回目录

---

 题目：

 解题思路：

我现在还挺厉害的，一遍过

 1 def numberOfArithmeticSlices(self, A):
 2         """
 3         :type A: List[int]
 4         :rtype: int
 5         """
 6         n = len(A)
 7         i = j = 0
 8         res = 0
 9         while j < n:
10             while i + 2 < n:
11                 if A[i+1]-A[i] == A[i+2]-A[i+1]:
12                     break
13                 else:
14                     i += 1
15             j = i + 2
16             while jand (A[j]-A[j-1] == A[j-1]-A[j-2]):
17                 res += j-i-1
18                 j += 1
19             i = j   
20         return res

 

我是以j为终点，到j的可行方案就是 j-i-1

相同的时间复杂度，但是更为简洁的代码：

参考答案

 1 def numberOfArithmeticSlices(self, A):
 2         """
 3         :type A: List[int]
 4         :rtype: int
 5         """
 6         curr = 0
 7         res = 0
 8         n = len(A)
 9         for i in range(2,n):
10             if A[i]-A[i-1] == A[i-1]-A[i-2]:
11                 curr += 1
12                 res += curr
13             else:
14                 curr = 0
15         return res

 

 

 

 

 

 

 

---

416. Partition Equal Subset Sum 【Medium】   返回目录

---

 题目：

解题思路：

这其实是个求和问题，看数组中能否挑出数字的和为 target = sum/2 

dp[target+1]

for num in nums:

for i in range(target,0,-1):

dp[i] = dp[i] or dp[i-num]

 为什么不顺着来，因为顺着来的话比如 [1,2,5]   dp[2] = dp[1] 划分成1+1不对

这样前面的不会重复

def canPartition(self, nums):
        """
        :type nums: List[int]
        :rtype: bool
        """
        sums = sum(nums)
        if sums & 1:
            return False
        target = sum(nums)//2
        dp = [False for i in range(target+1)]
        dp[0] = True
        for num in nums:
            for i in range(target,num-1,-1):
                dp[i] = dp[i] or dp[i-num]
        return dp[target]

 

 

 

 

 

---

418. Sentence Screen Fitting 【Medium】【Locked】   返回目录

---

 题目：

解题思路：

 说是Google的面试题

参考答案的解法：用start变量来记录下能装下的句子的总长度，最后除以一个句子的长度(带空格)，就可以得到个数。

而句子的总长度的求法时需要在每个单词后面加上一个空格，包括最后一个单词，遍历屏幕的每一行，然后每次start都加上宽度，看all[start%len]是否为空格，如果是start+1,

 这个算法不容易理解，想到这个算法的人真的是太牛了。

 1 def wordsTyping(sentence, rows, cols):
 2         s = " ".join(sentence)
 3         s += " "
 4         n = len(s)
 5         start = 0
 6         for i in range(rows):
 7             start += cols
 8             if s[start % n] == " ":
 9                 start += 1
10                 continue
11             while start>0 and s[(start-1)%n]!=' ':
12                 start -= 1
13         return start // n

 

 

 

 

 

 

 

 

---

464. Can I Win 【Medium】  返回目录

---

 题目：

解题思路：

对于Game playing的题目，用top-down DP做，每一个暴力的例子都是一种可能的游戏状态

这种方式要注意的点就是注意不要重复求解子问题，时间复杂度可以从O(n!) 变到 O(2^n)  二叉树的子节点

what is the state of the game?

 参考了一个答案，如下：

 

 1 class Solution:
 2     def canIWin(self, maxChoosableInteger, desiredTotal):
 3         """
 4         :type maxChoosableInteger: int
 5         :type desiredTotal: int
 6         :rtype: bool
 7         """
 8         if (1 + maxChoosableInteger)*maxChoosableInteger/2 < desiredTotal:
 9             return False
10         self.memo = {}
11         return self.helper(range(1,maxChoosableInteger+1),desiredTotal)
12     
13     def helper(self, nums,desiredTotal):
14         nums = list(nums)
15         hash_num = str(nums)
16         if hash_num in self.memo:
17             return self.memo[hash_num]
18         if nums[-1] >= desiredTotal:
19             return True
20         for i in range(len(nums)):
21             if not self.helper(nums[:i]+nums[i+1:], desiredTotal-nums[i]):
22                 self.memo[hash_num] = True
23                 return True
24         self.memo[hash_num] = False
25         return False

 

 

 

 

 

 

 

 

---

 467. Unique Substrings in Wraparound String 【Medium】   返回目录

---

 题目：

解题思路：

和之前有道题很相似，这里我给出了一种解法：

 1 def findSubstringInWraproundString(self, p):
 2         """
 3         :type p: str
 4         :rtype: int
 5         """
 6         n = len(p)
 7         res = len(set(p))
 8         i = j = 0
 9         for j in range(i+1,n):
10             if ord(p[j]) == ord(p[j-1])+1 or ord(p[j]) == ord(p[j-1])-25:
11                 res += (j-i)
12             else: 
13                 i = j
14         return res

通过样例21/81不能通过abaab这种带重复的样例

一下给出正确代码：

def findSubstringInWraproundString(self, p):
        """
        :type p: str
        :rtype: int
        """
        count = [0 for i in range(26)]
        maxLengthCur = 0
        for i in range(len(p)):
            if i > 0 and (ord(p[i]) == ord(p[i-1])+1 or ord(p[i]) == ord(p[i-1])-25):
                maxLengthCur += 1
            else:
                maxLengthCur = 1
            index = ord(p[i]) - ord('a')
            count[index] = max(count[index],maxLengthCur)
        
        res = 0
        for i in range(26):
            res += count[i]
        return res

或者

def findSubstringInWraproundString(self, p):
        """
        :type p: str
        :rtype: int
        """
        count = [0 for i in range(26)]
        res = length = 0
        for i in range(len(p)):
            cur = ord(p[i]) - ord('a')
            if i > 0 and ord(p[i-1])!=(cur+26-1)%26+ord('a'):
                length = 0
            length += 1
            if length > count[cur]:
                res += length - count[cur]
                count[cur] = length
        return res

 

 

 

 

 

---

474. Ones and Zeroes  【Medium】  返回目录

---

 题目:

 

 解题思路：

用dp[i][j]表示用i个0和j个1能组成的字符串个数

dp[i][j] = max(dp[i-zeros][j-ones]+1, dp[i][j])

注意到一个细节，如果单词正好由i个0和j个1组成，就会在本来的基础上进行吧加一操作，所以是逐渐累加的过程

 

code:

 1 def findMaxForm(self, strs, m, n):
 2         """
 3         :type strs: List[str]
 4         :type m: int
 5         :type n: int
 6         :rtype: int
 7         """
 8         dp = [[0]*(n+1) for i in range(m+1)]
 9         for s in strs:
10             zeros, ones = s.count('0'),s.count('1')
11             for i in range(m,zeros-1,-1):
12                 for j in range(n,ones-1,-1):
13                     dp[i][j] = max(dp[i-zeros][j-ones]+1, dp[i][j])
14         return dp[m][n]

上面代码python2不会超时，python3会超时，不是很懂

 

 

 

 

 

 

 

---

486. Predict the Winner 【Medium】   返回目录

---

 

题目：

 

 解题思路：

这道题不太会做，直接看的答案，不知道如何设计dp数组

看了答案，发现这种交替的任务还是应该看成同一个问题，同一种操作，也就是是说都是挑最大的score，只不过对手挑的时候取个负值

dp[i,j]=nums[i]−dp[i+1][j],nums[j]−dp[i][j−1].

 code:

 1 def PredictTheWinner(self, nums):
 2         """
 3         :type nums: List[int]
 4         :rtype: bool
 5         """
 6         n = len(nums)
 7         dp = [[0]*n for i in range(n+1)]
 8         for i in range(n,-1,-1):
 9             for j in range(i+1, n):
10                 a = nums[i] - dp[i+1][j]
11                 b = nums[j] - dp[i][j-1]
12                 dp[i][j] = max(a,b)
13         return dp[0][n-1] >= 0

 

 

 

 

 

---

494. Target Sum  【Medium】  返回目录

---

题目：

 

 

 解题思路：

对于这里动态规划题型，主要就是要写出它的状态转移方程，也就是要自己定义好 dp[i][j] 其中i, j的意义，以及 dp[i][j]的意义

通常情况下dp[i][j]是指要求的答案，i,j 是要自己设计它的意义，这里可以设i为  选择[0,i]个元素  j是指 和为j

dp[i][j]表示 使用前i个数 的和达到 j 的总的方法数

那么，

dp[i][j] = dp[i-1][j-num[i]] + dp[i-1][j+num[i]] 

边界条件是 初始全部为0 dp[0][num[0]] = 1   矩阵大小为 [len(num), max(sum(num),target)]

j-num[i]  或者  j+num[i] 是要大于0的

 

问题，对于第一个取负的情况处理不了  下面这个没有处理负数情况

 1 def findTargetSumWays(self, nums, S):
 2         """
 3         :type nums: List[int]
 4         :type S: int
 5         :rtype: int
 6         """
 7         n = len(nums)
 8         m = max(sum(nums),S)
 9         dp = [[0]*(m+1) for i in range(n)]
10         dp[0][nums[0]] = 1
11         for i in range(1,n):
12             for j in range(m+1):
13                 if j-nums[i]>=0:
14                     dp[i][j] += dp[i-1][j-nums[i]]
15                 if j+nums[i] <= m:
16                     dp[i][j] += dp[i-1][j+nums[i]]
17         print(dp)
18         return dp[n-1][S]

 

code:  利用上题目给出的限制条件，

1. The sum of elements in the given array will not exceed 1000.

 1 def findTargetSumWays(self, nums, S):
 2         """
 3         :type nums: List[int]
 4         :type S: int
 5         :rtype: int
 6         """
 7         n = len(nums)
 8         dp = [[0]*2001 for i in range(n)]
 9         dp[0][nums[0]+1000] = 1
10         dp[0][-nums[0]+1000] += 1
11         for i in range(1,n):
12             for j in range(-1000,1001):
13                 if dp[i-1][j+1000]>0:
14                     dp[i][j+nums[i]+1000] += dp[i-1][j+1000]
15                     dp[i][j-nums[i]+1000] += dp[i-1][j+1000]
16         return 0 if S>1000 else dp[n-1][S+1000]

 

 

 

 

---

 516. Longest Palindromic Subsequence 【Medium】  返回目录

---

 

题目：

 

解题思路：

如果 c[i] == c[j]

dp[i][j] = dp[i+1][j-1] + 2

else: dp[i][j] = max(dp[i+1][j], dp[i][j-1])

 

code：

 1 def longestPalindromeSubseq(self, s):
 2         """
 3         :type s: str
 4         :rtype: int
 5         """
 6         n = len(s)
 7         dp = [[1 if j==(i+1) else 0 for j in range(n+1)] for i in range(n)]
 8         for i in range(n-2,-1,-1):
 9             for j in range(i+2,n+1): 
10                 if s[i] == s[j-1]:
11                     dp[i][j] = dp[i+1][j-1] + 2
12                 else:
13                     dp[i][j] = max(dp[i][j-1],dp[i+1][j])
14         return dp[0][n]

 

 

这个代码超时了，不懂为什么

code: JAVA Accepted

 1 public class Solution {
 2     public int longestPalindromeSubseq(String s) {
 3         int[][] dp = new int[s.length()][s.length()];
 4         
 5         for (int i = s.length() - 1; i >= 0; i--) {
 6             dp[i][i] = 1;
 7             for (int j = i+1; j < s.length(); j++) {
 8                 if (s.charAt(i) == s.charAt(j)) {
 9                     dp[i][j] = dp[i+1][j-1] + 2;
10                 } else {
11                     dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);
12                 }
13             }
14         }
15         return dp[0][s.length()-1];
16     }
17 }

 

 

 

---

523. Continuous Subarray Sum 【Medium】  返回目录

---

 题目：

 

 解题思路：

暴力搜索，就会超时，以下是暴力搜索

code:

 1 def checkSubarraySum(self, nums, k):
 2         """
 3         :type nums: List[int]
 4         :type k: int
 5         :rtype: bool
 6         """
 7         n = len(nums)
 8         for i in range(n-1):
 9             for j in range(i+1,n):
10                 temp = sum(nums[i:j+1])
11                 if not k:
12                     if not temp:
13                         return True
14                     else:
15                         return False
16                 elif temp % k == 0:
17                     return True
18         return False

 

 

 看了下解题答案，真是太厉害了，用O(n)的时间复杂度只扫一遍就可以确定

用hashmap记录下 累积到当前位置的和 mod k的余数对应的位置i

如果累积和到位置j mod k相应余数和之前 位置i的相应余数相同，那么就说明 i-j之间的累积和 是k的倍数，注意在python中 hashmap用 dict表示

code:

 1 def checkSubarraySum(self, nums, k):
 2         """
 3         :type nums: List[int]
 4         :type k: int
 5         :rtype: bool
 6         """
 7         hashmap = {0:-1}
 8         temp = 0
 9         for i in range(len(nums)):
10             temp += nums[i]
11             if k!=0:
12                 temp = temp % k
13             if temp in hashmap:
14                 if i - hashmap[temp] > 1:
15                     return True
16             else:
17                 hashmap[temp] = i
18         return False

 

这里还有个值的注意的点就是它对于0的处理，这里初始化为0 ： -1

所以，对于  [0,0] 0 的情况是正确的

 

 

 

 

---

576. Out of Boundary Paths 【Medium】   返回目录

---

 

题目：

解题思路：

什么情况下可以跨越边界，就是在倒数第一步的时候就在边界旁边，所以设置dp[i][j] 表示当前步数到（i,j）位置可能的path数目， 那么下一步的 (i,j) 位置就是上一步的它的上下左右位置的path数之和

 code:

 1 def findPaths(self, m, n, N, i, j):
 2         """
 3         :type m: int
 4         :type n: int
 5         :type N: int
 6         :type i: int
 7         :type j: int
 8         :rtype: int
 9         """
10         M = 10**9 + 7
11         dp = [[0]*n for i in range(m)]
12         dp[i][j] = 1
13         count = 0
14         for k in range(1,N+1):
15             temp = [[0]*n for i in range(m)]
16             for i in range(m):
17                 for j in range(n):
18                     if i == m - 1:
19                         count = (count + dp[i][j]) % M
20                     if j == n - 1:
21                         count = (count + dp[i][j]) % M
22                     if i == 0:
23                         count = (count + dp[i][j]) % M
24                     if j == 0:
25                         count = (count + dp[i][j]) % M
26                     temp[i][j] = ((dp[i-1][j] if i>0 else 0) + (dp[i+1][j] if ielse 0) + (dp[i][j-1] if j>0 else 0) + (dp[i][j+1] if j < n-1 else 0)) % M
27             dp = temp[:][:]
28         return count

 

 

 

---

638. Shopping Offers 【Medium】  返回目录

---

 

题目：

 

解题思路：

不会做，只能看答案了

code:

 1 def shoppingOffers(self, price, special, needs):
 2         """
 3         :type price: List[int]
 4         :type special: List[List[int]]
 5         :type needs: List[int]
 6         :rtype: int
 7         """
 8         d = {}
 9         def dfs(cur):
10             val = sum(cur[i]*price[i] for i in range(len(needs))) #cost without special
11             for spec in special:
12                 tmp = [cur[j] - spec[j] for j in range(len(needs))]
13                 if min(tmp) >= 0: 
14                     val = min(val, d.get(tuple(tmp), dfs(tmp)) + spec[-1]) 
15             d[tuple(cur)] = val
16             return val
17         return dfs(needs)

 

 

 

 

---

646. Maximum Length of Pair Chain 【Medium】  返回目录

---

 题目：

 

 解题思路：

首先 sort一遍这个列表，按照第二位数字的值进行升序排序

dp[i]表示以i 结尾的 最长的chain长度，那么

dp[i] = dp[nums[i][0]] + 1

code:

 1 def findLongestChain(self, pairs):
 2         """
 3         :type pairs: List[List[int]]
 4         :rtype: int
 5         """
 6         pairs.sort()
 7         dp = [1] * len(pairs)
 8 
 9         for j in range(len(pairs)):
10             for i in range(j-1,-1,-1):
11                 if pairs[i][1] < pairs[j][0]:
12                     dp[j] = max(dp[j], dp[i] + 1)
13                     break
14         return max(dp)

 

 看答案，用greedy贪心算法也行，有点像之前学的那个教室排课的算法(时间快了很多很多)

1 def findLongestChain(self, pairs):
2     cur, res = float('-inf'), 0
3     for p in sorted(pairs, key=lambda x: x[1]):
4         if cur < p[0]: cur, res = p[1], res + 1
5     return res

 

 

 

 

---

647. Palindromic Substrings 【Medium】  返回目录

---

 题目：

解题思路：

之前做过找最长的回文子序列，所以这道题很容易就能做出来

用dp[i][j] 表示  i,j是否可以构成回文子序列

code:

 1 def countSubstrings(self, s):
 2         """
 3         :type s: str
 4         :rtype: int
 5         """
 6         n = len(s)
 7         dp = [[1 if j==(i+1) or j==i else 0 for j in range(n+1)] for i in range(n)]
 8         for i in range(n-2, -1, -1):
 9             for j in range(i+2,n+1):
10                 if s[i] == s[j-1]:
11                     dp[i][j] = dp[i+1][j-1]
12         return sum(sum(i) for i in dp) - n

 

 

 

---

650. 2 Keys Keyboard 【Medium】  返回目录

---

 

题目：

 

 解题思路：

不会做，看了答案

可以把这个问题形式化成一个素数分解问题

code:

 1 def minSteps(self, n):
 2         """
 3         :type n: int
 4         :rtype: int
 5         """
 6         ans = 0 
 7         d = 2
 8         while n > 1:
 9             while n % d == 0:
10                 ans += d
11                 n /= d
12             d += 1
13         return ans

 

 

 

 

 

---

651. 4 Keys Keyboard 【Medium】  返回目录  [locked]

---

题目：

 

 

解题思路：

 

code:

1 def maxA(self, N):
2         best = [0, 1]
3         for k in xrange(2, N+1):
4             best.append(max(best[x] * (k-x-1) for x in xrange(k-1)))
5             best[-1] = max(best[-1], best[-2] + 1) #addition
6         return best[N]

 

 

 

 

---

 673. Number of Longest Increasing Subsequence  【Medium】  返回目录

---

 题目：

 解题思路：

查看答案：

code:

 1 def findNumberOfLIS(self, nums):
 2         N = len(nums)
 3         if N <= 1: return N
 4         lengths = [0] * N #lengths[i] = longest ending in nums[i]
 5         counts = [1] * N #count[i] = number of longest ending in nums[i]
 6 
 7         for j, num in enumerate(nums):
 8             for i in xrange(j):
 9                 if nums[i] < nums[j]:
10                     if lengths[i] >= lengths[j]:
11                         lengths[j] = 1 + lengths[i]
12                         counts[j] = counts[i]
13                     elif lengths[i] + 1 == lengths[j]:
14                         counts[j] += counts[i]
15 
16         longest = max(lengths)
17         return sum(c for i, c in enumerate(counts) if lengths[i] == longest)

 

 

 

 

 

 

---

688. Knight Probability in Chessboard  【Medium】   返回目录

---

 

题目：

 

 解题思路：

利用两个棋盘，其中一个保存上一步的情况，每一个位置都是这一步在这个位置的概率，最后对棋盘求个总和就行

 

代码看的答案，写的非常好

code:

 1 def knightProbability(self, N, K, r, c):
 2         """
 3         :type N: int
 4         :type K: int
 5         :type r: int
 6         :type c: int
 7         :rtype: float
 8         """ 
 9         dp = [[0] * N for _ in xrange(N)]
10         dp[r][c] = 1
11         for _ in xrange(K):
12             dp2 = [[0] * N for _ in xrange(N)]
13             for r, row in enumerate(dp):
14                 for c, val in enumerate(row):
15                     for dr, dc in ((2,1),(2,-1),(-2,1),(-2,-1),
16                                    (1,2),(1,-2),(-1,2),(-1,-2)):
17                         if 0 <= r + dr < N and 0 <= c + dc < N:
18                             dp2[r+dr][c+dc] += val / 8.0
19             dp = dp2
20 
21         return sum(map(sum, dp))

 

 

 

 

---

698. Partition to K Equal Sum Subsets 【Medium】   返回目录

---

 题目：

 

 

 

 

 

 

 

---

 712. Minimum ASCII Delete Sum for Two Strings 【Medium】    返回目录

---

 题目：

 

 

 

---

 740. Delete and Earn 【Medium】   返回目录

---

 题目：

 

转载于:https://www.cnblogs.com/lainey/p/8084643.html